Глава 8. Элементы квантовой механики
Глава 7. Корпускулярно-волновые свойства материи
Тепловое излучение
· Основные характеристики теплового излучения:
1) поток излучения – это величина, равная энергии, переносимой излучением в единицу времени через какую-либо поверхность:  ;
;
2) энергетическая светимость(интегральная плотность потока излучения)– это величина, равная энергии, испускаемой в единицу времени единицей поверхности излучающего тела по всем направлениям: 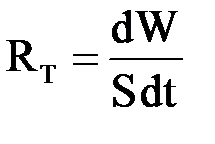 ;
;
3) спектральная плотность энергетической светимости тела (испускательная способность тела) - это величина, равная энергии, испускаемой единицей поверхности излучающего тела в единицу времени по всем направлениям, приходящаяся на единичный интервал частот (длин волн):
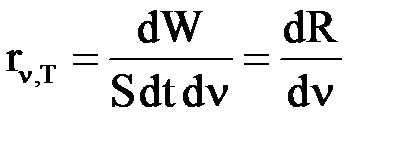 ;
;  ,
,
где испускательные способности  и
и  связаны соотношением
связаны соотношением  ;
;
4)спектральный коэффициент поглощения (поглощательная способность тела)  (или
(или  ) - это отношение потока излучения, поглощенного телом в некотором малом интервале частот (или длин волн), к потоку падающего на тело излучения в том же интервале частот (или длин волн).
) - это отношение потока излучения, поглощенного телом в некотором малом интервале частот (или длин волн), к потоку падающего на тело излучения в том же интервале частот (или длин волн).
· Законы теплового излучения:
1) Закон Кирхгофа: отношение испускательной и поглощательной способности тела является для всех тел универсальной функцией частоты (или длины волны) и температуры (функцией Кирхгофа):
 (или
(или  ).
).
Так как для абсолютно черного тела  (или
(или  ), то функция Кирхгофа представляет собой испускательную способность АЧТ
), то функция Кирхгофа представляет собой испускательную способность АЧТ  и
и  .
.
2) Закон Стефана-Больцмана: энергетическая светимость абсолютно черного тела (АЧТ) пропорциональна четвертой степени его абсолютной температуры
 ,
,
где  - постоянная Стефана-Больцмана.
- постоянная Стефана-Больцмана.
Для любого нагретого тела
 ,
,
где величина  называется степенью черноты.
называется степенью черноты.
3) Закон смещения Вина: длина волны  , соответствующая максимальному значению спектральной плотности энергетической светимости
, соответствующая максимальному значению спектральной плотности энергетической светимости  АЧТ, обратно пропорциональна его абсолютной температуре
АЧТ, обратно пропорциональна его абсолютной температуре
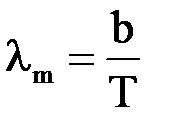 ,
,
где  - постоянная Вина.
- постоянная Вина.
· Формулы Рэлея-Джинса и Планка.
1) Формула Рэлея –Джинса для функции Кирхгофа:
 ,
,
2) Формула Планка для функции Кирхгофа:
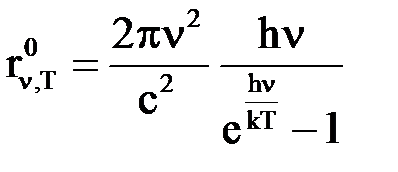 .
.
· Энергия фотона  ;
;  , где
, где  - частота колебаний в волне,
- частота колебаний в волне,  - циклическая частота колебаний в волне;
- циклическая частота колебаний в волне;  - постоянная Планка;
- постоянная Планка;  .
.
· Масса фотона  .
.
· Импульс фотона  или
или  , или
, или 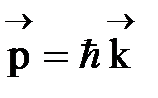 , где
, где  - волновой вектор,
- волновой вектор, 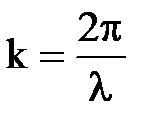 .
.
Внешний фотоэффект
· Уравнение Эйнштейна для внешнего фотоэффекта
 ,
,
где  - работа выхода электрона;
- работа выхода электрона;  - максимальная кинетическая энергия электрона, вышедшего из вещества.
- максимальная кинетическая энергия электрона, вышедшего из вещества.
«Красная граница» определяется условием  , то есть
, то есть  .
.
В релятивистском случае  ,следовательно,
,следовательно,
 и
и
 .
.
· Метод задерживающих потенциалов.
При изменении частоты падающего на катод излучения меняется величина задерживающей разности потенциалов, что позволяет определить постоянную Планка:
 (1)
(1)
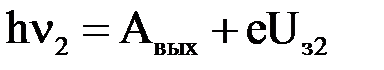 (2)
(2)
После вычитания из выражения (2) выражения (1), получим:
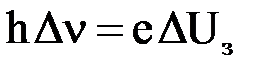 , откуда
, откуда 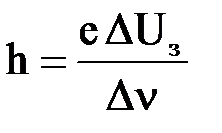 .
.
Эффект Комптона
· Изменение длины волны фотона в эффекте Комптона
 ,
,
где 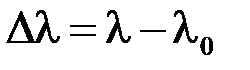 ,
,
 - длина волны излучения от источника,
- длина волны излучения от источника,
 - длина волны рассеянного излучения,
- длина волны рассеянного излучения,
 - коэффициент пропорциональности, называемый комптоновская длина волны той частицы, масса которой находится в знаменателе; для электрона
- коэффициент пропорциональности, называемый комптоновская длина волны той частицы, масса которой находится в знаменателе; для электрона  =2,43пм.
=2,43пм.
· Давление, производимое светом при нормальном падении  , где
, где  - объемная плотность энергии излучения;
- объемная плотность энергии излучения;  - коэффициент отражения.
- коэффициент отражения.
Глава 8. Элементы квантовой механики
· Соотношения неопределенностей Гейзенберга:
- для координаты и импульса частицы
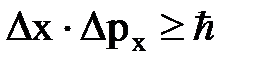 ,
,
где  - неопределенность проекции импульса на ось
- неопределенность проекции импульса на ось  ;
; 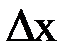 - неопределенность ее координаты;
- неопределенность ее координаты;
- для энергии и времени
 ,
,
где  - неопределенность энергии данного квантового состояния;
- неопределенность энергии данного квантового состояния; 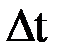 - время пребывания системы в этом состоянии.
- время пребывания системы в этом состоянии.
· Общее уравнение Шредингера.
 ,
, 
где  - оператор Лапласа;
- оператор Лапласа;
 - функция, характеризующая силовое поле, в котором частица движется, - имеет смысл потенциальной энергии.
- функция, характеризующая силовое поле, в котором частица движется, - имеет смысл потенциальной энергии.
Если силовое поле не зависит от времени, то 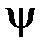 -функцию можно представить сомножителями
-функцию можно представить сомножителями
 .
.
Независимую от времени функцию  можно найти, решая стационарное уравнение Шредингера:
можно найти, решая стационарное уравнение Шредингера:
 ,
,
где  - постоянная, которая, как можно показать, имеет смысл полной энергии частицы.
- постоянная, которая, как можно показать, имеет смысл полной энергии частицы.
· Свободное движение микрочастицы.
- потенциальная функция микрочастицы  ;
;
- уравнение Шредингера (стационарное)  ;
;
- решение стационарного уравнения Шредингера  ;
;
- полное уравнение Шредингера:  ;
;
- решение полного уравнения Шредингера:  .
.
· Движение микрочастицы вблизи потенциального барьера ступенчатой формы:
- коэффициент прозрачности для прямоугольного потенциального барьера конечной ширины:
 ,
,
где  - высота барьера;
- высота барьера;  - его ширина.
- его ширина.
- коэффициент прозрачности для непрямоугольного барьера:
 ,
,
где 
 .
.
· Микрочастица в прямоугольной потенциальной яме:
- стационарное уравнение Шредингера для области внутри ямы:
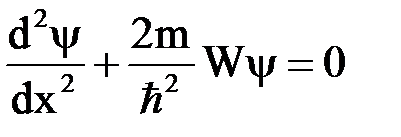 или
или  ;
;
- решение уравнения Шредингера для этой области:
 ,
,
где  ;
;
- длина волны де Бройля в области ямы:  , откуда
, откуда  , то есть число
, то есть число  соответствует числу полуволн де Бройля, укладывающихся на ширине ямы;
соответствует числу полуволн де Бройля, укладывающихся на ширине ямы;
- импульс и энергия частицы в яме имеют дискретные спектры:
 ;
;  ;
;
- расстояние между соседними уровнями:
 .
.
· Квантовый (одномерный) гармонический осциллятор:
- потенциальная функция:
 ,
,
где  - собственная частота колебаний осциллятора;
- собственная частота колебаний осциллятора;
- стационарное уравнение Шредингера:
 ;
;
- собственные функции (решения, удовлетворяющие требованиям, предъявляемым к  -функции) имеют вид
-функции) имеют вид
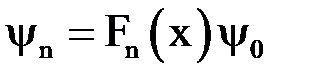 ,
,
где  - полиномы
- полиномы  -ой степени;
-ой степени;  ;
;
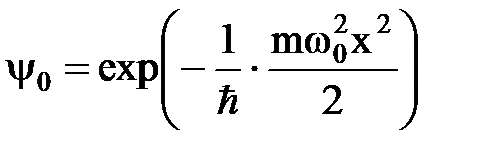 -
-
-  -функция наиболее низкого энергетического состояния при
-функция наиболее низкого энергетического состояния при  ;
;
- энергия наиболее низкого состояния: 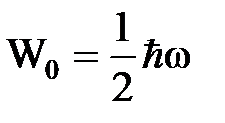 .
.
Энергия следующих состояний возрастает на величину  , то есть энергетический спектр гармонического осциллятора также дискретен
, то есть энергетический спектр гармонического осциллятора также дискретен
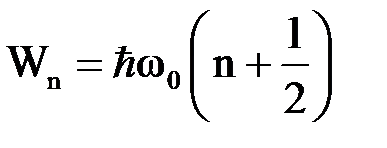 ,
,
где  .
.
Дата добавления: 2016-01-05; просмотров: 24; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
