при курсах Ki ≥ K2 судно будет пересекать линию перемещения циклона позади его штормовой зоны.

⇐ ПредыдущаяСтр 2 из 2

Если полное уклонение от штормовой зоны оказывается невозможным, то следует уклоняться от наиболее опасного сектора тропического циклона (правый задний сектор циклона в Северном полушарии, левый задний сектор циклона в Южном полушарии), где скорость ветра складывается со скоростью перемещения циклона.

При отсутствии достоверной информации сторона штормовой зоны, в которой оказалось судно, определяется по наблюдаемому изменению ветра: изменение направления ветра вправо (влево) указывает, что судно находится в правой (в левой) по ходу циклона половине штормовой зоны, а при постоянстве направления и усилении ветра судно находится на линии перемещения циклона.

Следует подчеркнуть, что уклонение от опасных гидрометеоявлений целесообразно даже для крупных современных судов. Подавляющее число случаев гибели отечественных морских грузовых транспортных судов за 1970 — 1990 гг. связано со штормовыми условиями плавания. При вынужденном попадании в штормовые условия необходимо правильно выбирать курсы и скорости судна по отношению к волне с использованием универсальной диаграммы качки, а при усилении волнения — своевременно переходить к штормованию.

Локсодромия

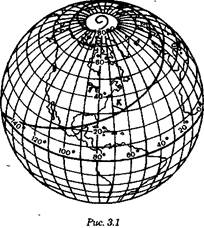С появлением на морских судах магнитных компасов стало удобно плавать по линии постоянного курса, что стимулировало геометрические исследования в этой области. Кривую на поверхности Земли, пересекающую все меридианы под одним и тем же углом, назвали локсодромией, что с греческого переводится как «косой бег». Ее вид на поверхности сферы представлен на рис. 3.1. Для формального описания локсодромии применяется тот же математический аппарат, что и для описания картографической проекции Меркатора, эти вопросы тесно связаны между собой.

Расстояние между двумя точками на сфере по локсодромии не является кратчайшим и ее применение в мореплавании объясняется исключительным удобством использования компасов. Эта кривая чрезвычайно важна в практике навигации.

Название локсодромия данная кривая имеет, в основном, в сферической геометрии и навигации, а в математике она известна под более общим названием — логарифмическая спираль. Это одна из замечательных математических кривых, у которой радиус-вектор составляет постоянный угол с касательной к ней в любой точке. В навигационной терминологии этот угол между истинным меридианом и носовой частью ДП судна называют истинным курсом.

Рис. 3.1 дает возможность увидеть основные свойства локсодромии:

1.Если К = 0 или 180°, то очевидно, что локсодромия совпадает с меридианом, т. е. с большим кругом;

2.Если К = 90 или 270°, то локсодромия совпадает с параллелью или экватором, т. е. образует малый или большой круг на поверхности сферы;

3.При любых других курсах локсодромия спиралеобразно стремится к полюсу, никогда его не достигая.

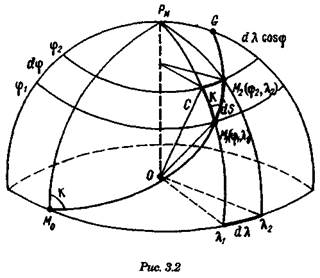Теперь, когда принципиальное поведение локсодромии на сфере нам понятно, приступим к ее формальному изучению.

Выведем уравнение кривой на поверхности сферы. Для этого рассмотрим рис. 3.2, на котором изображен отрезок локсодромии, пересекающей меридианы под углом К. Выберем на локсодромии две точки M1(φ1, λ1) и
М2 (φ2, λ2), разделенные элементарным расстоянием ds друг от друга, и проведем через них параллели и меридианы. Таким образом, на сфере зафиксирован элементарный треугольник М1М2С, в котором

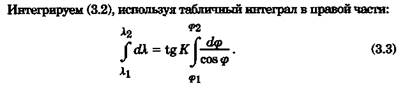
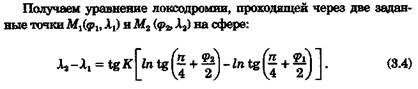
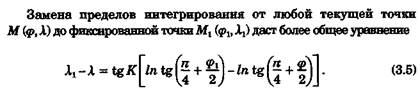
После получения уравнения локсодромии можно сделать анализ ее свойств, не прибегая к рис. 3.1, как было сделано выше. Проверим эти свойства кривой по уравнению (3.4).

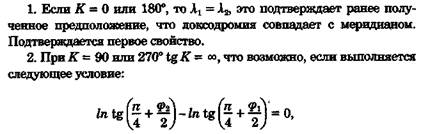
а это выполнимо при φ1 = φ2, т. е. когда локсодромия совпадает с параллелью или экватором и образует малый или большой круг на поверхности сферы. Второе свойство также подтверждается.

Это уравнение логарифмической спирали. Для каждой ∆λ, отличающейся от предыдущей на 2π,
т. е. ∆λi+1=∆λi+n2π, φ2 будет иметь новое значение. Таким образом, локсодромия пересекает каждый меридиан бесчисленное количество раз, изменяя широту, и стремится к полюсу, никогда его не достигая. Итак, и третье свойство локсодромии имеет четкое формальное доказательство.

Напишем уравнение локсодромии с учетом сжатия Земли, поэтому трансформируем (3.3) для поверхности эллипсоида. Для этого необходимо в правую часть уравнения ввести выражения для главных радиусов кривизны земного эллипсоида М и N:

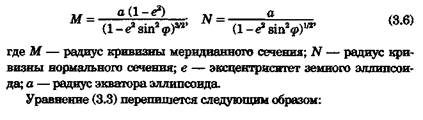
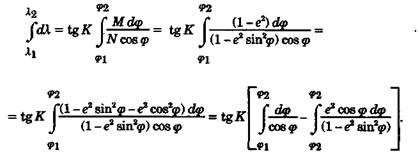
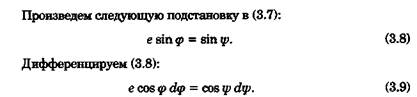
Таким образом, когда М = N, т. е. в случае решения задачи на поверхности шара, за уравнение локсодромии отвечает интеграл I, а в случае эллипсоида вводится дополнительный интеграл J:

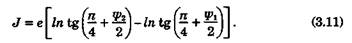
Произведем обратную замену переменных. Элементарные тригонометрические соотношения позволяют получить следующие формулы:

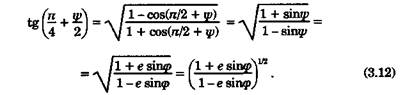
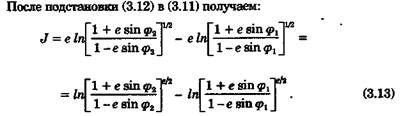
Теперь, подставив (3.13) в (3.10) и осуществив операцию потенцирования, напишем уравнение локсодромии для эллипсоида

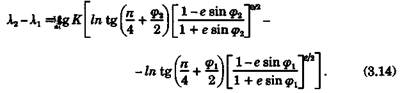
Дата добавления: 2016-01-05; просмотров: 1; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!