Изотермический процесс.
Изотермический процесс. Процесс, протекающий при постоянной температуре, называется изотермическим. Уравнение изотермического процесса в системе координат Т — s T = соnst.
Изотерма на диаграмме Т — s представлена прямой, параллельной оси абсцисс (оси s). Подставляя T = соnst в уравнение состояния идеального газа, получим 
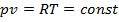для конечного процесса 1 — 2 
. При изотермическом процессе объем газа обратно пропорционален давлению (закон Бойля — Мариотта). В соответствии с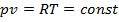
изотерма на диаграмме р — vпредставляет равнобокую гиперболу. Запишем уравнения для дифференциалов внутренней энергии и энтальпии: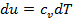 
; 
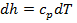. Для изотермического процесса(dT=0) получаем: 
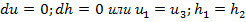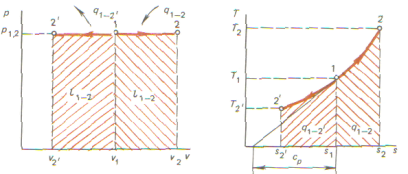
. Внутренняя энергия и энтальпия в изотермическом процессе не изменяются. Из первого закона термодинамики dq=dl получаем для процесса 1—2: 
. Количество теплоты, сообщенной газу в изотермическом процессе, численно равно работе расширения. Для рассматриваемого процесса коэффициент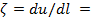 
0. Теплота идет на эквивалентное возмещение внутренней энергии системы, за счет которой совершается работа расширения. Работа изменения объема в процессе 1 - 2: 
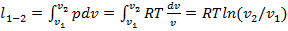. Полезная внешняя работа в изотермическом процессе равна работе расширения, так как 
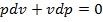, поэтому 
. Для процесса 1 — 2 
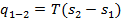, или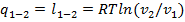 
. Теплоемкость в изотермическом процессе 
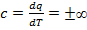. Изменение энтропии в процессе 1— 2 определится из уравнения 
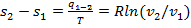или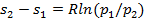 
.
Изобарный процесс.
Изобарный процесс. Изобарный процесс —
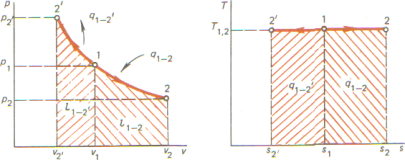
процесс, протекающий при постоянном давлении газа (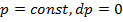 
). Изобара на диаграмме р — vпредставлена прямой, параллельной оси абсцисс. Из уравнения состояний Клапейрона при 
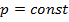следует 
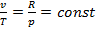, для процесса 1— 2 
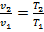. В изобарном процессе объем газа пропорционален термодинамической температуре (закон Гей-Люссака). Уравнение первого закона термодинамики представим следующим образом: 
.
Для изобарного процесса последнее уравнение перепишется так: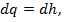 
для процесса 1-2 
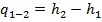. Теплота, сообщаемая газу в изобарном процессе, идет на увеличение его энтальпии. Работа изменения объема в процессе 1-2 
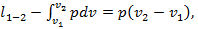или учитывая, что 
, 
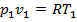, а 
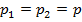, получим 
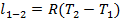. При разности температур 
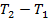в один кельвин газовая постоянная является работой расширения, совершаемой в изобарном процессе 1 кг газа. Количество теплоты, полученной газом в изобарном процессе 
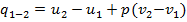. Коэффициент 𝜁 для изобарного процесса определяется по формуле 
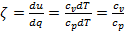. Илн, если принять 
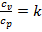, где k-показатель адиабаты, 𝜁=1/k. Например, при k= 1,4 (для воздуха) 𝜁=0,715. Это означает, что 71,5% сообщаемой газу теплоты идет на изменение его внутренней энергии, а 28,5 % расходуется на совершение работы расширения. Уравнение изобары в системе координат Т — s можно получить из зависимостей: 
; 
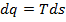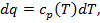откуда для процесса 1- 2 получаем 
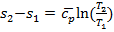. Изобара на диаграмме T-s представлена логарифмической кривой. Под касательная к изобаре на этой диаграмме в любой точке в определенном масштабе представляет собой истинную изобарную теплоемкость ср. Удельное количество теплоты 
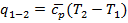, а так как 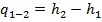, оно равно изменению энтальпии газа 
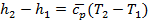. Соотношения 
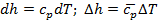справедливы для всех процессов идеального газа.
В процессе 1-2теплота подводится, газ расширяется, увеличиваются температура и энтропия газа, в процессе 1—2' теплота отводится, газ сжимается, температура и энтропия уменьшаются.
Подставим в уравнения первого закона термодинамики соотношение, характерное для изобарного процесса pdv=RdT. Разделив полученное выражение на d Т, получаем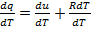 
, откуда 
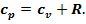Это уравнение Р. Майера. Из него видно, что удельная изобарная теплоемкость всегда больше удельной изохорной на газовую постоянную.
Изохорный процесс.
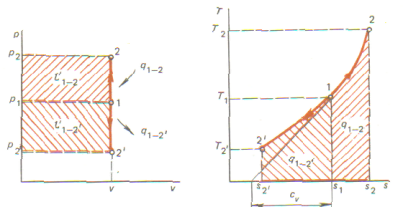
Изохорный процесс. Изохорный процесс - процесс. происходящий при постоянном объеме газа: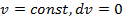 
. В соответствии с данным уравнением изохорный процесс изображается на диаграмме р-v вертикальной прямой. Эта линия называется изохорой (линия 1– 2 - теплота подводится, давление возрастает; линия 1-2' - теплота отводится, давление уменьшается). Из уравнения состояния идеального газа для изохорного процесса 
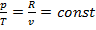, или для процесса 1-2 
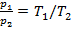. В изохорном процессе давление газа пропорционально термодинамической температуре. Это соотношение представляет собой закон Шарля. Запишем уравнение первого закона термодинамики в виде 
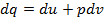. Для изохорного процесса работа изменения объема не совершается, так как dl=pdv=0. Поэтому последнее уравнение принимает вид dq=du, или для процесса 1-2 
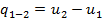. Теплота, сообщаемая газу или отведенная от него в изохорном процессе, идет на изменение внутренней энергии (𝜁=1). При подведении теплоты внутренняя энергия газа увеличивается, при отведении - уменьшается. Элементарное количество теплоты при изохорном процессе 
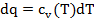или 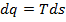, откуда, приравнивая правые части уравнений, определяем изменение энтропии 
, или для процесса 1-2: 
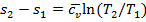. График изохорного процесса на диаграмме Т - s представляет логарифмическую кривую (кривая 1-2 - тепло подводится, энтропия и температура возрастают; кривая 1- 2' —тепло отводится, энтропия и температура уменьшаются). Количество теплоты, сообщаемое газу или отводимое от него в процессе 1-2 (2'), 
; .
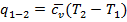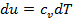Внутренняя энергия идеального газа во всех процессах, протекающих в одном и том же интервале температур, изменяется на одну и ту же величину независимо от характера процесса. Вследствие этого выражение 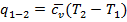; справедливо для всех процессов идеального газа.
На диаграмме Т-s подкасательная к кривой процесса в любой ее точке определяет истинное значение удельной изохорной теплоемкости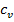 
. Причем чем больше теплоемкость 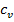, тем более полого проходит кривая процесса. Полезная внешняя работа 
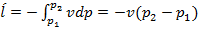. Изменение энтальпии в изохорном процессе определяем из уравнения 
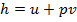. Дифференцируем это выражение: 
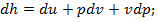получаем (pdv=0) 
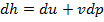, для процесса 1-2 
, или 
.
Дата добавления: 2015-12-17; просмотров: 104; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!