в) дисперсиясын ықшамдап табу.
Егер теріс емес бүтін мәндер қабылдайтын ξ кездейсоқ шамасының үлестірімі
P(ξ=k)=  (1)
(1)
Қатынастарымен анықталса, мұндағы параметр λ>0, онда біз мұндай кездейсоқ шаманы параметірі λ -ға тең. Пуассондық кездейсоқ шама деп атайтын және оны бұдан былай қарай қысқаша ξ~П(λ) түрінде жазатын боламыз.
Әрине, 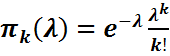 ықтималдықтары үшін
ықтималдықтары үшін 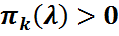 және
және  Кей жағдайларда бізге дискретті кездейсоқ шаманы келесідей кесте түрінде берген ыңғайлы (
Кей жағдайларда бізге дискретті кездейсоқ шаманы келесідей кесте түрінде берген ыңғайлы (
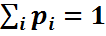 )
)
1-кесте
| ξ – дің мәндері (ξ) | 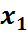
| 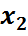
| … | 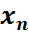
| … |
| Мәндерді қабылдаудың сәйкес ықтималдықтары (P) | 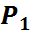
| 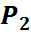
| … | 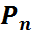
| … |
ξ~П(λ).Онда
М ξ= 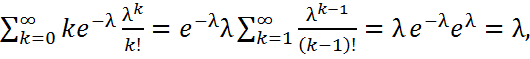
М ξ(ξ-1)= 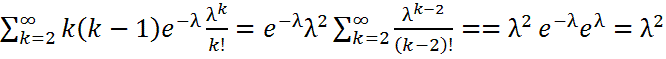 Демек, D ξ=
Демек, D ξ=  . Сонымен ξ~П(λ) үшін М ξ= D ξ=
. Сонымен ξ~П(λ) үшін М ξ= D ξ= 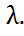
| 19.Кездейсоқ вектор (көп өлшемді кездейсоқ шама) а) Екі өлшемді кездейсоқ вектор, оныңың үлестірімі. б) Екі өлшемді кездейсоқ вектордың үлестірім функциясының негізгі төрт қасиетін дәлелдеу в) Маргинал үлестірімдер және оларды вектордың үлестірімінен шығару |
Анықтама. 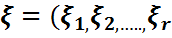 ) векторы кездейсоқ вектор немесе r-өлшемді (көп өлшемді) кездейсоқ шама деп аталады, ал мына ықтималдықтар
) векторы кездейсоқ вектор немесе r-өлшемді (көп өлшемді) кездейсоқ шама деп аталады, ал мына ықтималдықтар
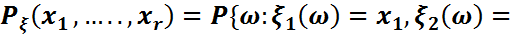
 (1)
(1)
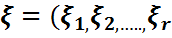 кездейсоқ векторының ықтималдық үлестірім заңы деп немесе
кездейсоқ векторының ықтималдық үлестірім заңы деп немесе 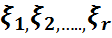 кездейсоқ шамаларының бірлескен үлестірімі (бірлескен үлестірім заңы) деп аталады
кездейсоқ шамаларының бірлескен үлестірімі (бірлескен үлестірім заңы) деп аталады
|
|
|
r=2 жағдайын қарастырайық. Онда  кездейсоқ шамаларының бірлескен үлестірім заңын(екі өлшемді үлестірім заңын) мынадай таблица арқылы беруге болады:
кездейсоқ шамаларының бірлескен үлестірім заңын(екі өлшемді үлестірім заңын) мынадай таблица арқылы беруге болады:
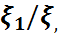
| x21 | x22 | … | x2n2 | … |
| x11 | P11 | P12 | … | P1n2 | … |
| x12 | P21 | P22 | … | P2n2 | … |
| … | … | … | … | … | … |
| x1n1 | P n11 | P n12 | … | P n1n2 | … |
| … | … | … | … | … | … |
Бұл таблицада 1-баған мен 1-жатық жолда сәйкес  кездейсоқ шамаларының қабылдайтын мәндері жазылған, ал pij=P{
кездейсоқ шамаларының қабылдайтын мәндері жазылған, ал pij=P{ 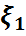 =x1i,
=x1i, 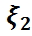 =x2j} және pij≥0,
=x2j} және pij≥0, 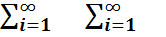 pij=1
pij=1
Бұл функция (әр аргументі) бойынша кемімейді (FF1 қасиеті), айнымалылар жиынтығы бойынша оң жағынан үзіліссіз (FF3қасиеті);F(+ 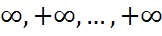 )=1 егер y=
)=1 егер y= 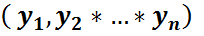
нүктесінің ең болмағанда бір координатасы 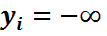 болса, онда
болса, онда 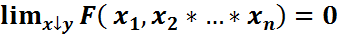 (FF2 қасиеті). Бұлардан басқа бұл функция келесі теріс емес анықталғандық деп аталатын қасиеті қанағаттандырады: FF4
(FF2 қасиеті). Бұлардан басқа бұл функция келесі теріс емес анықталғандық деп аталатын қасиеті қанағаттандырады: FF4 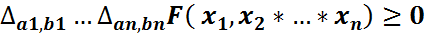 мұндағы
мұндағы 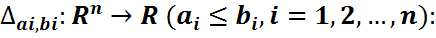
 айырымдық операторы
айырымдық операторы 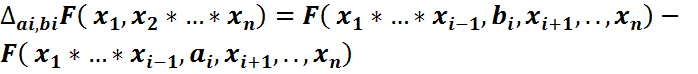 қатынасымен анықталған оператор. Алғашқы үш қасиет (FF1,FF2,FF3қасиеттері) бір өлшемді жағдайдағыға ұқсас әдістермен оп-оңай дәлелденеді.Енді F4 қасиетін дәлелдейік. Қарапайымдылық үшін n=2 болсын.Онда
қатынасымен анықталған оператор. Алғашқы үш қасиет (FF1,FF2,FF3қасиеттері) бір өлшемді жағдайдағыға ұқсас әдістермен оп-оңай дәлелденеді.Енді F4 қасиетін дәлелдейік. Қарапайымдылық үшін n=2 болсын.Онда 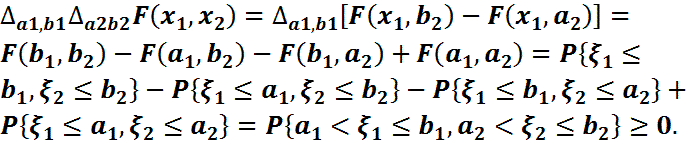 Жалпы жағдай осыған ұқсас дәлелденеді, бізге тек
Жалпы жағдай осыған ұқсас дәлелденеді, бізге тек 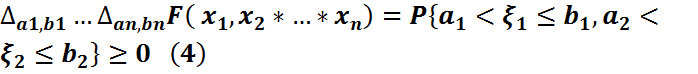 болатындығын байқау жеткілікті.
болатындығын байқау жеткілікті.
|
|
|
Теорема: Айталық F(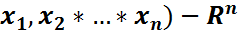 кеңістігінде анықталған көп өлшемді үлестірім функциясы болсын. Онда қандай да бір
кеңістігінде анықталған көп өлшемді үлестірім функциясы болсын. Онда қандай да бір 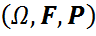 ықтималдық кеңістік және бұл кеңістікте анықталған қандай да бір
ықтималдық кеңістік және бұл кеңістікте анықталған қандай да бір 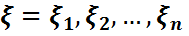 кездейсоқ шамалары табылады да, берілген F(
кездейсоқ шамалары табылады да, берілген F(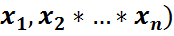 функциясы осы көп өлшемді
функциясы осы көп өлшемді 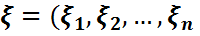 ) кездейсоқ шамасының бірлескен үлестірім функциясы болады:
) кездейсоқ шамасының бірлескен үлестірім функциясы болады: 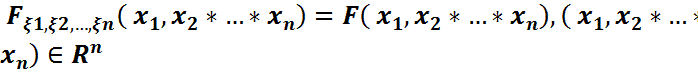 .Сол сияқты
.Сол сияқты  көп өлшемді үлестірім функциясы
көп өлшемді үлестірім функциясы  үлестірім заңын бірмәнді анықтайды. Сонымен бірге, кез келген i=1,2,..n үшін{
үлестірім заңын бірмәнді анықтайды. Сонымен бірге, кез келген i=1,2,..n үшін{ 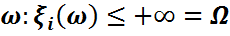 болуы себепті, егер көп өлшемді
болуы себепті, егер көп өлшемді 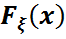 үлестірім функциясының қандай да бір
үлестірім функциясының қандай да бір  координаталардан +
координаталардан +  ұмтылса, онда сәйкес кездейсоқ вектордың осы координаталардан басқа бір
ұмтылса, онда сәйкес кездейсоқ вектордың осы координаталардан басқа бір  компоненталарынан тұртан вектордың үлестірім функциясы шығатынын, яғни
компоненталарынан тұртан вектордың үлестірім функциясы шығатынын, яғни 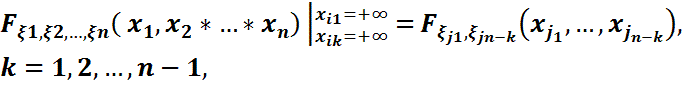 мұндағы
мұндағы 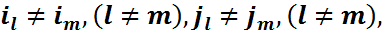 және {
және { 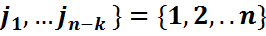 \{
\{ 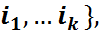 қатынастары дұрыс болатынын байқау қиын емес. Соңғы қатынастың оң жағындағы үлестірімдер n-k өлшемді маргиналды үлестірім деп аталады. Түсінікті болу үшін кейбір жекелеген жағдайларды жазып көрсетейік:
қатынастары дұрыс болатынын байқау қиын емес. Соңғы қатынастың оң жағындағы үлестірімдер n-k өлшемді маргиналды үлестірім деп аталады. Түсінікті болу үшін кейбір жекелеген жағдайларды жазып көрсетейік: 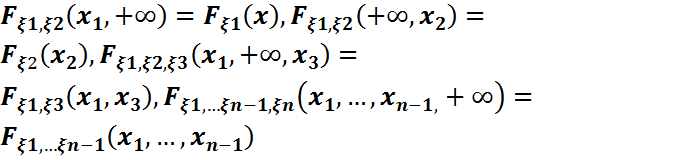 , т.с.с.
, т.с.с.
| 20,Үлкен сандар заңы а) Марков теңсіздігі. б)Чебышев теңсіздігі. в)Үлкен сандар заңының Чебышев тұжырымдамасы және дәлелдеу. |
1 теорема. (Беpнулли схемасы үшін үлкен сандар заңы).Кез келген 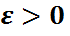 үшін
үшін
|
|
|
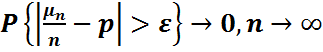 (1)
(1)
Дәлелдеу. Чебышев теңсіздігі бойынша  Чебышев теңсіздігін
Чебышев теңсіздігін 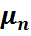 кездейсоқ шамасының 4 – моментіне пайдалану арқылы (1) – қатынастан күштірек мынадай тұжырымжы дәлелдей аламыз.
кездейсоқ шамасының 4 – моментіне пайдалану арқылы (1) – қатынастан күштірек мынадай тұжырымжы дәлелдей аламыз.
2-теорема. (Бернулли схемасы үшін күшейтілген үлкен сандар заңы). Кез келген 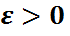 үшін
үшін
P{  }
} 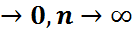 (2)
(2)
Дәлелдеу. Былай жаза аламыз: P{  }=P{
}=P{ 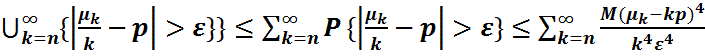 }
} 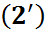
Соңғы теңсіздікті біз Чебышев теңсіздігін 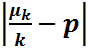 кездейсоқ шамасының 4-моментіне қолдану арқылы жаздық.Енді (
кездейсоқ шамасының 4-моментіне қолдану арқылы жаздық.Енді (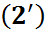 – формуланың оң жағындағы 4-моментіне ашып жазайық.
– формуланың оң жағындағы 4-моментіне ашып жазайық.
M 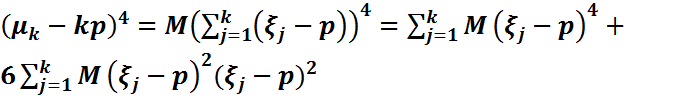 . Біз бұл жерде
. Біз бұл жерде 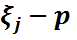 кездейсоқ шамаларының тақ дәрежелерін қамтитын индекстері әртүрлі көбейтінділер үшін сәйкес математикалық күтімдер нөлге тең болатынын пайдаландық. Ары қарай, тағы да мультипликативтік қасиет бойынша, i
кездейсоқ шамаларының тақ дәрежелерін қамтитын индекстері әртүрлі көбейтінділер үшін сәйкес математикалық күтімдер нөлге тең болатынын пайдаландық. Ары қарай, тағы да мультипликативтік қасиет бойынша, i 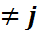 үшін
үшін 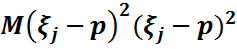 =
= 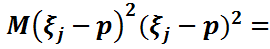 D
D 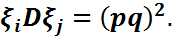 Сонымен қатар M
Сонымен қатар M 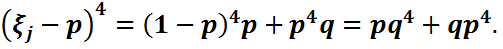 Сондықтан,
Сондықтан, 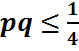 болатынын ескерсек, M
болатынын ескерсек, M 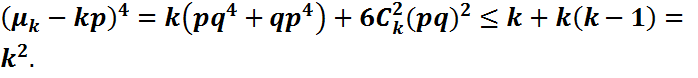 Демек P{
Демек P{  }
} 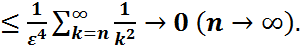
Чебышев теңсіздігі
Егер 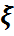 теріс емес кездейсоқ шама (
теріс емес кездейсоқ шама (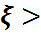 0) болса, онда кез-келген
0) болса, онда кез-келген 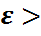 0 саны үшін P{
0 саны үшін P{ 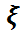 ≥
≥ 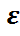 }≤
}≤ 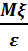
|
|
|
Дәлелдеу. 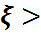 0 үшін мына теңсіздіктер тізбесін жаза аламыз:
0 үшін мына теңсіздіктер тізбесін жаза аламыз:
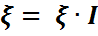 {
{ 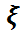 ≥
≥ 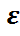 }+
}+ 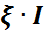 {
{ 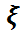 ≥
≥ 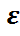 }≥
}≥ 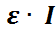 {
{ 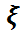 ≥
≥ 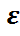 }
}
Бұдан, математикалық күтімнің теріс еместік қасиеті бойынша M  ≥ M(
≥ M(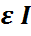 {
{ 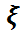 ≥
≥ 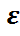 })=
})= 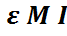 {
{ 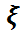 ≥
≥ 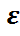 }=
}= 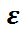 P{
P{ 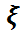 ≥
≥ 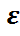 }
}
Марков теңсіздігі.
ξ: Ω→R M (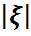 )<+
)<+  болсын.
болсын.
Онда: 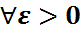
 P(
P(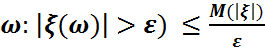
Дәлелдеу: Дискрет жағдайда
М(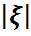 ) =
) = 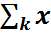 k pξ(xk)
k pξ(xk)
P (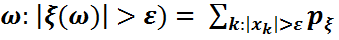 (xk)
(xk)
| 21. | Тәуелсіз оқиғалар а) Екі оқиға тәуелсіздігінің анықтамасы. Мысал. б) n оқиға жағдайы: қос-қостан тәуелсіздік және жиынтық тәуелсіздік. б)Бернштейн мысалы. |
Тәуелсіз оқиғалар анықтамасы:
1-анықтама. Егер А және В оқиғаларының көбейтіндісінің ықтималдығы олардың ықтималдықтарының көбейтіндісіне тең болса, яғни Р(АВ) Р(А)Р(В) қатынасы орындалса, онда мұндай оқиғаларды тәуелсіз оқиғалар деп атаймыз.
2-анықтама. 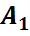 ,
, 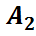 ,…,
,…, 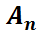 оқиғалары (
оқиғалары (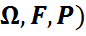 ықтималдық кеңістігінде анықталған оқиғалар болсын. Егер кез келген 1
ықтималдық кеңістігінде анықталған оқиғалар болсын. Егер кез келген 1 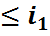 <
< 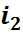 <…<
<…< 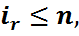 r=2,3,…,n индекстері үшін P(
r=2,3,…,n индекстері үшін P(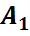 ,
, 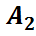 ,…,
,…, 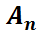 )= P(
)= P(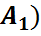 P(
P(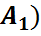 … P(
… P(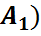
шарттары орындалатын болса, онда біз 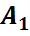 ,
, 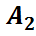 ,…,
,…, 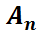 оқиғаларын тәуелсіз оқиғалар деп атаймыз.
оқиғаларын тәуелсіз оқиғалар деп атаймыз.
Қос-қостан тәелсіздік және жиынтық тәуелсіздік.Бернштейн мысалы.
( ,Ғ,Р)-ықтималдық кеңістігі берілсін,онда А1,А2,...,Аn (n
,Ғ,Р)-ықтималдық кеңістігі берілсін,онда А1,А2,...,Аn (n 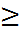 3)-оқиғалары қарастырылсын.
3)-оқиғалары қарастырылсын.
Анықтама:1)Егер 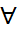 i,j(i
i,j(i 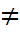 j) үшін P(Ai,Aj)=P(Ai)P(Aj) болса,онда А1,А2,...,Аn оқиғалары қос-қостан тәуелсіз
j) үшін P(Ai,Aj)=P(Ai)P(Aj) болса,онда А1,А2,...,Аn оқиғалары қос-қостан тәуелсіз
2) 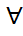 к=2,3,..., n және
к=2,3,..., n және 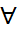 i1, i2,..., iк әртүрлі (i1
i1, i2,..., iк әртүрлі (i1 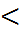 i2
i2 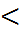 ...
... 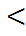 iк) үшін
iк) үшін
Р(Аi1,Ai2,…,Aik)=P(Ai1)P(Ai2)…P(Aik)
Теңдіктері орындалса,онда А1,А2,...,Аn оқиғалары жиынтықты тәуелсіз болады.
Сn2+Cn3+…+Cnk
Бұл анықтамадан тәуелсіз жиынтыкты тәуелсіздіктен қос-қостан тәуелсіздік шығатыны көрініп тұр.Ал кері жағдай орындалмайды.
Бернштейн мысалы.
Жәшікте 2,3,5 және 30 сандарымен нөмірленген төрт шар бар.
Сынақ-кездейсоқ біреуін таңдау.
А1-(таңдалған шар нөмері 2-ге еселі)
А2-(таңдалған шар нөмері 3-ке еселі)
А3-(таңдалған шар нөмері 5-ке еселі)
1)Осы оқиғаларды қос-қостан тәуелсіз болуын тексеру
2)Жиынтықты тәуелсіз болама?
 =4
=4
A1={2,30}, 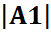 =2, P(A1)=1/2
=2, P(A1)=1/2
A2={3,30}, 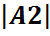 =2, P(A2)=1/2
=2, P(A2)=1/2
A3={5,30},  =2, P(A3)=1/2
=2, P(A3)=1/2
P(A1A2)=1/4
P(A2A3)=1/4 -қос-қостан тәуелсіз
Р(A1A3)=1/4
Р(A1A2А3)=1/4 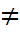 P(A1) P(A2) P(A3) – жиынтық тәуелсіз емес.
P(A1) P(A2) P(A3) – жиынтық тәуелсіз емес.
| 22. | Көрсеткішті үлестірім: а) анықтамасы және қолоданылу мысалы б) оның математикалық күтімін есептеуге қысқаша формула қорыту в) оның дисперсиясын есептеуге қысқаша формула қорыту |
η үлестірім функциясы F(x) болатын үзіліссіз кездесоқ шама болсын. Егер механизмнің а уақыт жұмыс істеген белгілі болса,онда оның қалған жұмыс істеу уақытының үлестірім функциясы қалай анықталады?
Бізге P{η-a 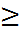 x/η
x/η 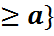 ықтималдығын табу жеткілікті. Біз былай жаза аламыз:
ықтималдығын табу жеткілікті. Біз былай жаза аламыз:
P{ η-a 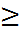 x/η
x/η  =
= 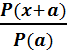 =
= 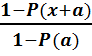
η-ның үлестірімін кқрсеткіштік үлестірімін есептейміз. Бірақ көрсеткіштік үлестірім үшін F(x)=1- 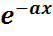 (x
(x 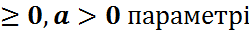 ) болатынын ескерсек, онда жоғарыдағы қатынастар Р(x)=
) болатынын ескерсек, онда жоғарыдағы қатынастар Р(x)= 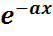 үлестірілгендігін аламыз.
үлестірілгендігін аламыз.
Көрсеткіштік үлестірім (өзінің дискретті аналогы P{e=k}=qk(1-q) k=0.1…)үлестірім функциясының барлық қасиеттеріне ие жалғыз үлестірім болатын байқау қиын емес. Ал сонғы қатынастан шығатын:
P(x+a)=P(x)*P(a)
функционалдық теңдеуінің салдары.
| 23. | Үзіліссіз кездейсоқ шамалар: а) Анықтамасы, үлестірім тығыздығы. б)Үлестірім функциясын тығыздық арқылы өрнектеу. Қасиеттері. в) Сынақ пен оған байланысты үзіліссіз кездейсоқ шама пайда болатын мысал |
Анықтама: Х кездейсоқ шамасы қабылдайтын мәндер шекті немесе шексіз интервалдың барлық мәндерін қабылдаса ол үзіліссіз кездейсоқ шама деп аталады.
Анықтама: Х кездейсоқ шамасының үлестірім функциясы F(x) деп Х˂х теңсіздігінің орындалу ықтималдығын айтады. F(x)=P(X˂x)
Қасиеттері: 1. Үлестірім F(x) функциясы оң, шектелген функция, яғни 0≤F(x)≤1. Бұлай болу себебі ол F(x) = P(X˂x) теңдігі бойынша ықтималдықты көрсетеді. Оның графигі y=0, y=1түзулері арасында орналасқан.
2. Үлестірім функциясы кемімейтін функция, яғни x1˂x2 болғанда F(x1) ≤ F(x2) болады. Шынында да x˂β оқиғасын x˂α және α≤x˂β оқиғаларының қосындысы деп қарастыруға болады. Сондықтан P(x˂β)=P(x˂α)+P(α≤x˂β)  P(α≤x˂β)=P(x˂β)-P(x˂α), P(α≤x˂β)=F(β)–F(α) (1) теңдігін аламыз. (1) теңдігін [x1,x2) аралығына қолдансақ, P(x1≤x˂x2)=F(x2)–F(x1) бұл теңдіктің сол жағы оң сан P(x1≤x˂x2)≥0 демек F(x2)– F(x1)≥0, F(x2)≥F(x1).
P(α≤x˂β)=P(x˂β)-P(x˂α), P(α≤x˂β)=F(β)–F(α) (1) теңдігін аламыз. (1) теңдігін [x1,x2) аралығына қолдансақ, P(x1≤x˂x2)=F(x2)–F(x1) бұл теңдіктің сол жағы оң сан P(x1≤x˂x2)≥0 демек F(x2)– F(x1)≥0, F(x2)≥F(x1).
3. Егер X кездейсоқ шамасының қабылдайтын мәндері тек (a,b) аралығында болса, x˂a мәндерінде F(x)=0 және x˃b мәндерінде F(x)=1 болады. Жалпы жағдайда, F(- 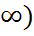 =0, F(+
=0, F(+ 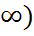 =1 болады деп есептеледі.
=1 болады деп есептеледі.
Анықтама: Х кездейсоқ шамасының үлестірім тығыздығы f(x) деп үлестірім F(x) функциясының туындысын айтады. 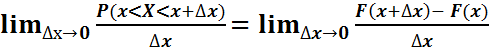 =F’(x)=f(x). Яғни үлестірім тығыздығы үлестірім функциясының туындысына тең. f(x)=F’(x)
=F’(x)=f(x). Яғни үлестірім тығыздығы үлестірім функциясының туындысына тең. f(x)=F’(x)
Қасиеттері: 1. Үлестірім тығыздығы теріс емес функция, себебі ол кемімейтін F(x) функциясының туындысына тең f(x)=F’(x)≥0.
2. Үлестірім функциясы үлестірім тығыздығы арқылы былай өрнектеледі F(x) = 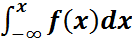 , шынында f(x)dx=dF(x) болғандықтан
, шынында f(x)dx=dF(x) болғандықтан 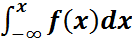 =
=  =F(x) = F(x) – F(-
=F(x) = F(x) – F(- 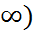 = F(x).
= F(x).
3. Кездейсоқ шаманың үлестірім тығыздығы f(x) болса, онда P(a ≤ X ˂ b) = 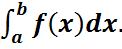 Шынында P(a ≤ X ˂ b) = F(b) – F(a) =
Шынында P(a ≤ X ˂ b) = F(b) – F(a) = 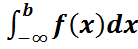 -
- 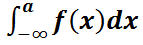 =
= 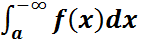 +
+ 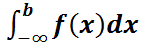 =
= 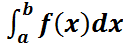 .
.
4. Үлестірім тығыздығы үшін 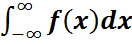 =1. ОХ өсімен және үлестірім тығыздығы y=f(x) қисығымен шектелген фигураның ауданы 1-ге тең болады.
=1. ОХ өсімен және үлестірім тығыздығы y=f(x) қисығымен шектелген фигураның ауданы 1-ге тең болады.
| 25. | Комбинаторика элементтері. а) n компонентті комбинация б)Шарларды жәшіктерге орналастыру в) Қайталанымды комбинациялар (Алыну реті ескерілетін қайтарымды таңдамалар). |
n компонентті комбинация деп n- дік деп
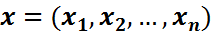
түрінде ашылып жазылатын 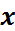 элементін айтады.
элементін айтады.  – бұл
– бұл  комбинациясының i- нші компоненті деп аталады.
комбинациясының i- нші компоненті деп аталады.
Теорема(комбинаториканың негізгі ережесі) n оң бүтін саны берілсін.
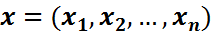
түріндегі әртүрлі комбинациялардан тұратын Х жиыны беріліп, келесі шарттар орындалса:
1) Х жиынындағы барлық комбинацияларды қарастырғанда, олардың 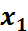 компоненті
компоненті 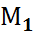 әр түрлі мән қабылдай алатын болса,
әр түрлі мән қабылдай алатын болса,
2)  компоненті бекітілген барлық комбинацияларды бөліп қарастырғанда, олардың
компоненті бекітілген барлық комбинацияларды бөліп қарастырғанда, олардың 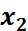 компоненті
компоненті 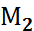 әр түрлі мән қабылдай алатын болса, және
әр түрлі мән қабылдай алатын болса, және 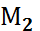 саны
саны 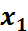 -дің барлық бекітулерінде бірдей болса,
-дің барлық бекітулерінде бірдей болса,
..........
3) n-1) 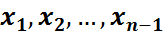 компоненттері бекітілген барлық комбинацияларды бөліп қарастырғанда, олардың
компоненттері бекітілген барлық комбинацияларды бөліп қарастырғанда, олардың 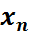 компоненті
компоненті 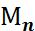 әр түрлі мән қабылдай алатын болса, және
әр түрлі мән қабылдай алатын болса, және 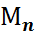 саны
саны 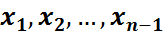 -дің барлық бекітулерінде бірдей болса,
-дің барлық бекітулерінде бірдей болса,
онда берілген Х жиынындағы барлық
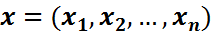
комбинацияларының саны 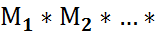
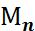 көбейтіндісіне тең болады.
көбейтіндісіне тең болады.
Алыну реті ескерілетін қайтарымды таңдамалар. Сынақ – бірінен соң бірі қайтарымды түрде 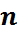 шар таңдау.
шар таңдау.
X={1,2,…,N} Оның қарапайым нәтижесі: 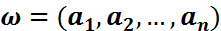 комбинациясы.
комбинациясы.
ЭОК 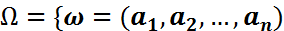 :
: 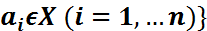 (1)
(1)
комбинациялар жиыны болып шығады.
| 26. | Нормаль үлестірім қасиеттері а) Нормаль үлестірілген өзара тәуелсіз екі кездейсоқ шаманың қосындысының үлестірімін қорыту.
б) Математикалық күтім
в) дисперсиясы
Параметрлері  және және 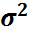 болатын болатын 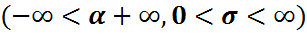 нормаль (гаустік, қалыпты) үлестірім: нормаль (гаустік, қалыпты) үлестірім:
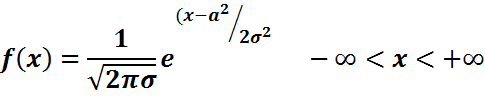 Мұндай қалыпты шаманы қысқаша
Мұндай қалыпты шаманы қысқаша 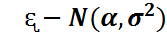 түрінде жазатын боламыз. Параметрлері түрінде жазатын боламыз. Параметрлері 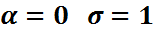 болатын нормаль үлестірім стандартты нормаль үлестірім деп аталады.
Нормальді үлестірімдердің композициясы нормальді үлестірілген болады. Осылай егер Х пен У – тәуелсіз нормальді үлестірілген кездейсоқ шамалар болса, яғни
Z болатын нормаль үлестірім стандартты нормаль үлестірім деп аталады.
Нормальді үлестірімдердің композициясы нормальді үлестірілген болады. Осылай егер Х пен У – тәуелсіз нормальді үлестірілген кездейсоқ шамалар болса, яғни
Z 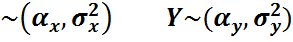 болса онда кездейсоқ шамасы да нормаль үлестірілген болады. Z болса онда кездейсоқ шамасы да нормаль үлестірілген болады. Z 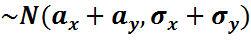 Х пен У тәуелді болса, (корреляция коэффициенті ρ≠0), онда Z=X+Y нормальді үлестірілген болып қалады, параметрлері
Х пен У тәуелді болса, (корреляция коэффициенті ρ≠0), онда Z=X+Y нормальді үлестірілген болып қалады, параметрлері
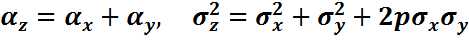
|
(Ω,ℱ, Р) ықтималдық кеңістігінде өзара тәуелсіз және үлестірімдері бірдей 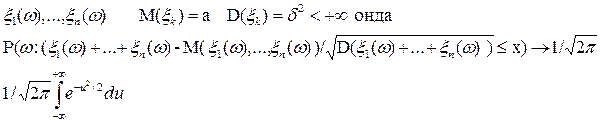
Муавр-Лаплас Ф0,1 (х) стандарт нормаль үлестірім эквивалентті N(0;1)
| 27. | Шартты ықтималдық а) Шартты ықтималдық анықтамасы. Мысал. б) Шартты ықтималдық қасиеттері в) Ықтималдықтарды көбейту формуласы. |
Анықтама. (Ω,F,P) –қандайда бір ықтималдық кеңістік, А және В ондағы оқиғалар және Р(B)>0 болсын В орындалады деп ұйғарғандағы А шартты ықтималдығы деп (P(AB))/(P(B)) санын атайды және оны Р_В (A) деп белгилейди.
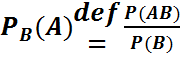
Шартты ықтималдық қасиеттері
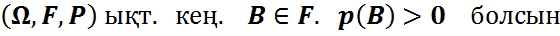
Онда
1) 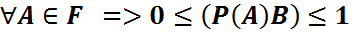
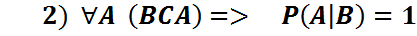

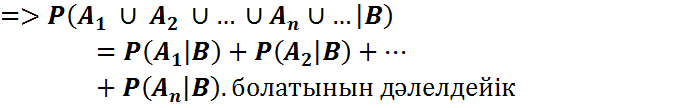
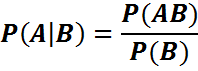
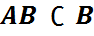
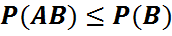
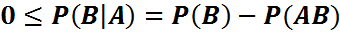
2) 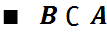
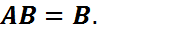
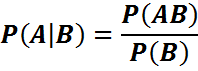
3) 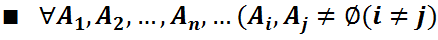
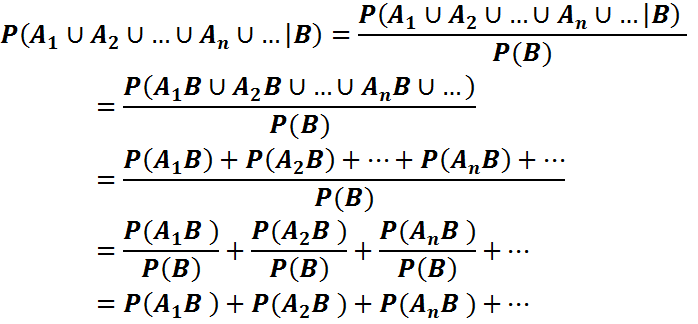
Ықтималдықтарды көбейту формуласы.
Шартты ықт.формуласыннан
P(A\B) =  =>
=>
P(AB) = P(B) P(A\B) немесе P(AB) = P(A) P(B\A)
Деген ықт-ды көбейту формуласын аламыз.
n-oқиға үшін:
P(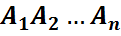 ) = P(
) = P(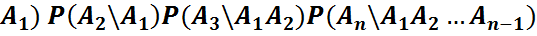
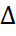 k=1,2,…,n-1
k=1,2,…,n-1
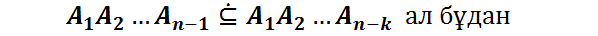
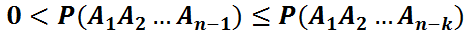 шығады.
шығады.
Мат.индукция арқылы
1) n=2 үшін
P 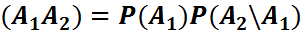 ақиқат
ақиқат
2) n=m-1 үшін:
P(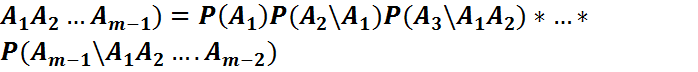 дұрыс деп ұйғарайық
дұрыс деп ұйғарайық
3) n=m үшін:
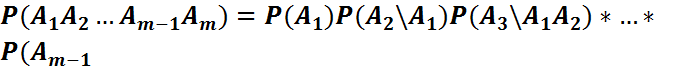 \
\ 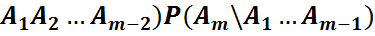
 A=
A= 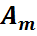 деп алайық.
деп алайық.
P(BA) = P(A) P(B\A) 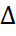
| 28. | Теріс биномиальді үлестірім а) анықтамасы және оған әкелетін мысал б) оның математикалық күтімін есептеуге қысқаша формула қорыту в) оның дисперсиясын есептеуге қысқаша формула қорыту. |
Табыс ықтималдығы p-ға тең Бернуллидің тәуелсіз сынақтар тізбегінде n-ші табыс n+k 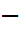 1-ші сынақта (k=0,1,2,…) пайдп болуының ықтималдығын табалық.
1-ші сынақта (k=0,1,2,…) пайдп болуының ықтималдығын табалық.
Егер n-ші табыс n+k-ші сынақта пайда болса, онда ең соңғы n+k-ші сынақта табыс (А оқиғасы), ал одан бұрыңғы n+k 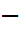 1 сынақта n
1 сынақта n 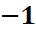 рет табыс, k рет сәтсіздік болды(В оқиғасы) деген сөз. Сынақтар тәуелсіз болғандықтан іздеп отырған ықтималдығымыз p(n,n+k)=P(AB)=P(B)P(A)=
рет табыс, k рет сәтсіздік болды(В оқиғасы) деген сөз. Сынақтар тәуелсіз болғандықтан іздеп отырған ықтималдығымыз p(n,n+k)=P(AB)=P(B)P(A)= 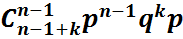 =
=  ,k=0,1,2,…(1) Бұл үлестірім теріс биномдық үлестірім деп аталады. Үлестірімнің атауы
,k=0,1,2,…(1) Бұл үлестірім теріс биномдық үлестірім деп аталады. Үлестірімнің атауы 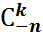 =
= 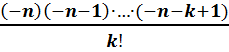 =
= 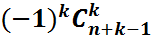 =
= 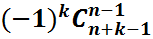 (2) теңдігіне байланысты шыққан. Соңғы теңдік (1)-үлестірімді p(n,n+k)=
(2) теңдігіне байланысты шыққан. Соңғы теңдік (1)-үлестірімді p(n,n+k)=  түрінде жазуға мүмкіндік береді. Ары қарай,
түрінде жазуға мүмкіндік береді. Ары қарай, 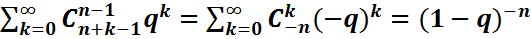 =
= 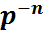 болғандықтан
болғандықтан 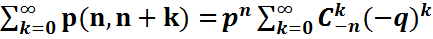 =
= 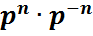 =1,
=1,
яғни 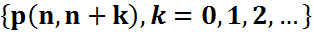 шындығында да ықтималдық үлестірім болады екен. Теріс биномдық үлестірімді кейде Паскаль үлестірімі деп те атайды. Ал n=1 болған кезде (1) үлестірім геометриялық үлестірім деп аталады.
шындығында да ықтималдық үлестірім болады екен. Теріс биномдық үлестірімді кейде Паскаль үлестірімі деп те атайды. Ал n=1 болған кезде (1) үлестірім геометриялық үлестірім деп аталады.
| 29. | Бернулли схемасындағы шектік теоремалар а) Муавр Лапластың локальді және интегралды формулалары (дәлелдеусіз). Бери -Эссеен бағасы б)Пуассонның жуықтау формуласы (дәлелдеу) в) Мысалдар |
Екі қарапайым нәтижесі бар сынақ берілсін, яғни екі элементар оқиғасы бар. Бір элементар оқиғаны «1» арқылы белгілеп, «табыс» деп аталсын. Екінші оқиғаны «0» арқылы белгілеп, «сәтсіздік» деп аталсын. Сонда элементар оқиғалар кеңістігі Ω={0;1}
P(1)=p (1)
P(0)=q, (0<p<1, q=1-p)
p саны табыс ықтималдығы деп, ал q – сәтсіздік деп аталады. (1) сынағын n рет тәуелсіз қайталау моделі:
Ω={ω=(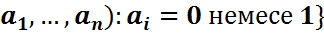
P=(ω=(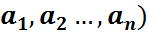 )=P(
)=P(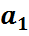 )
) 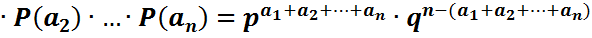 (2)
(2)
(2) моделін Бернулли схемасы деп атайды. Сонымен Бернулли схемасы дегеніміз – екі нәтижелі сынақты n рет тәуелсіз қайталаудың моделі.
Теорема. (Бернулли формулалары). (2) моделіндегі әрбір ω=(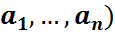 элементар оқиғасы үшін
элементар оқиғасы үшін 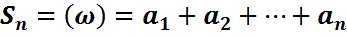 болсын(табыстар саны). Онда
болсын(табыстар саны). Онда
1) 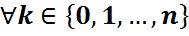 үшін
үшін
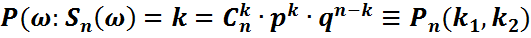 (3)
(3)
2) 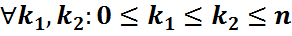 үшін
үшін
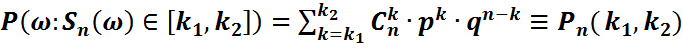 (4)
(4)
Мысал.Тиынды бес рет лақтырғанда үш рет гербтің түсу ықтималдығын табыңыз.
Шешуі. ЕНС моделі – тиынды бір лақтыру
Ω={0;1}
«1» - «герб» 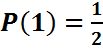 «0» - «цифр»
«0» - «цифр» 
Қайталау саны n=5 Табыстар саны 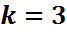
Онда (3) бойынша 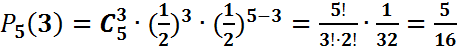
Бернулли схемасындағы ең ықтимал табыс саны
Бернулли схемасы үшін тәжірибені n рет қайталған кезде дәл k рет табыс болу (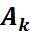 оқиғасы) ықтималдылығы
оқиғасы) ықтималдылығы
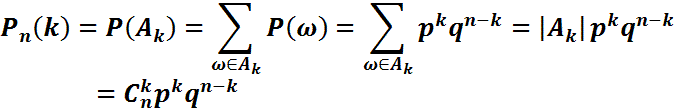

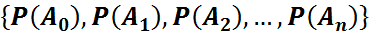 ықтималдылықтарының жиынтығы биномдық үлестірім (Көлемі n-ге тең таңдамадағы табыс санының биномдық үлестірімі) деп аталады.
ықтималдылықтарының жиынтығы биномдық үлестірім (Көлемі n-ге тең таңдамадағы табыс санының биномдық үлестірімі) деп аталады.
Пуассон теоремасы. А оқиғасының әрбір сынауда пайда болу ықтималдығы 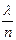 болса (
болса (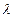 -тұрақты және п- нен тәуелсіз), онда өзара тәуелсіз п сынаудан құрылған серияда А оқиғасының дәл т рет пайда болу ықтималдығы
-тұрақты және п- нен тәуелсіз), онда өзара тәуелсіз п сынаудан құрылған серияда А оқиғасының дәл т рет пайда болу ықтималдығы

яғни  ; мұндағы
; мұндағы 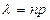 . мұны Пуассон формуласы деп атайды.
. мұны Пуассон формуласы деп атайды.
Муавр-Лапластың жергіліктік және интегралдық теоремалары. Қолданылу мысалдары.
1-теорема(Муавр-Лапластың жергіліктік теоремасы). Айталық, 0<p<1 болсын. Онда  қанағаттандыратын барлық
қанағаттандыратын барлық 
2-теорема.(Муавр-Лапластың интегралдық теоремасы). Табыс ықтималдылығы  әр n-ге сәйкес Бернулли схемасы берілсін. Онда
әр n-ге сәйкес Бернулли схемасы берілсін. Онда 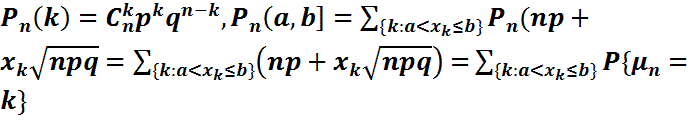 мұндағы
мұндағы  ал қосынды
ал қосынды 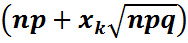 бүтін болатын
бүтін болатын 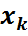 -лар бойынша алынатын болсын. Онда
-лар бойынша алынатын болсын. Онда 
| 30. | Хи-квадрат үлестірімі: а) анықтамасы б) оның математикалық күтімін есептеуге қысқаша формула қорыту в) оның дисперсиясын есептеуге қысқаша формула қорыту |
Анықтама: 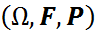 -ықтималдық кеңістігі берілсін.
-ықтималдық кеңістігі берілсін.
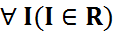 аралығы үшін
аралығы үшін
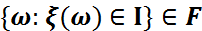
шартын қанағаттандыратын 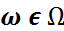 →
→  R функциясын кездейсоқ шама дейміз.
R функциясын кездейсоқ шама дейміз.
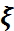 :
: 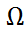 →
→  R кездейсоқ шамасының үлестірімі деп
R кездейсоқ шамасының үлестірімі деп
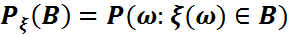
түріндегі ықтималдықтар жиынын айтады. Мұндағы B 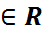 - аралықтар және олардың ақырлы, саналымды бірігулері түріндегі санды жиындар. Кездейсоқ шамасының үлестірімі оның қай аралықта мән қабылдау ықтималдығы қандай екенін көрсетеді.
- аралықтар және олардың ақырлы, саналымды бірігулері түріндегі санды жиындар. Кездейсоқ шамасының үлестірімі оның қай аралықта мән қабылдау ықтималдығы қандай екенін көрсетеді.
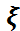 – бақыланатын кездейсоқ шамасы қалыпты үлестірілген, оның
– бақыланатын кездейсоқ шамасы қалыпты үлестірілген, оның 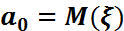 математикалық күтімі белгілі.
математикалық күтімі белгілі.
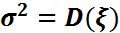 – дисперсиясы белгісіз
– дисперсиясы белгісіз
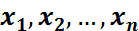 – таңдама.
– таңдама.
 тәуелсіз кездейсоқ шамалар, әрқайсысы қалыпты үлестірілген.
тәуелсіз кездейсоқ шамалар, әрқайсысы қалыпты үлестірілген.
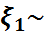 N(0,1), (i=1,…,n)
N(0,1), (i=1,…,n)
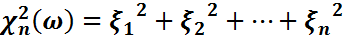
кездейсоқ шамасының үлестірімі хи – квадрат үлестірімі деп аталады.
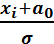
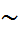 N(0,1) болады. Олай болса
N(0,1) болады. Олай болса 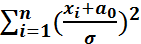 – үлестрімі Хи – квадрат (белгілі).
– үлестрімі Хи – квадрат (белгілі).
 – саны беріледі.
– саны беріледі.
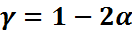 - маңыздылық деңгейі.
- маңыздылық деңгейі.
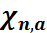 ,
, 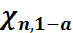 – сандарын мына теңдіктерден анықтайды:
– сандарын мына теңдіктерден анықтайды:
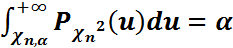 ,
, 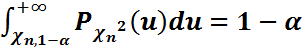 **
**
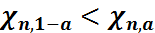
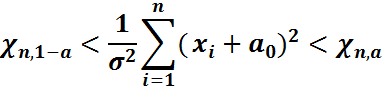
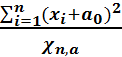 <
< 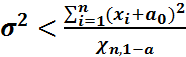
Бұл 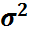 үшін маңыздылық деңгейі
үшін маңыздылық деңгейі 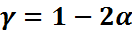 болатын сенімділік интервалы.
болатын сенімділік интервалы.
| 31. | Үзіліссіз кездейсоқ шаманың а) анықтамасы, үлестірімі, қасиеттері б)математикалық күтімі, қасиеттері в) дисперсиясы, қасиеттері. |
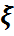 кездейсоқ шамасының математикалық күтімін мына Лебег –Стильтес интегралы арқылы есептеуге болады:
кездейсоқ шамасының математикалық күтімін мына Лебег –Стильтес интегралы арқылы есептеуге болады:  Егер
Егер 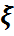 абсолютті үзіліссіз кездейсоқ шама боса және
абсолютті үзіліссіз кездейсоқ шама боса және 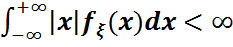 болса,мұндағы
болса,мұндағы 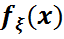 –
– 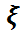 кездейсоқ шамасының үлестірім тығыздығы,онда
кездейсоқ шамасының үлестірім тығыздығы,онда 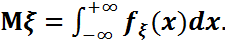 Егер
Егер 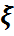 кездейсоқ шама,g=g(x) –борелдік функция болса,онда
кездейсоқ шама,g=g(x) –борелдік функция болса,онда 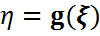 кездейсоқ шамасының математикалық күтімі:дискретті
кездейсоқ шамасының математикалық күтімі:дискретті 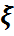 кездейсоқ шамасы үшін Mg(
кездейсоқ шамасы үшін Mg(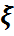 ) =
) = 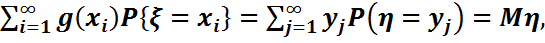 абсолютті үзіліссіз
абсолютті үзіліссіз 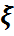 кездейсоқ шамасы үшін Mg(
кездейсоқ шамасы үшін Mg(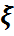 ) =
) = 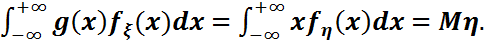
Қасиеттері(Математикалық күтім).(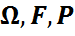 ) –ықтималдық кеңістікте
) –ықтималдық кеңістікте 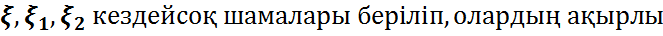 математикалық күтімдері бар болсын.
математикалық күтімдері бар болсын.
М1)М(k 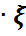 )=k
)=k  M(
M(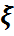 ), (
), (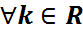 )
)
M2)Сызықты қасиеті М(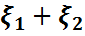 )=M(
)=M(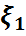 )+M(
)+M(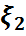 )
)
M3)Егер 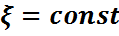 кездейсоқ шама болса,ол дегеніміз
кездейсоқ шама болса,ол дегеніміз 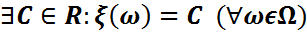 ,онда М(
,онда М(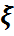 )=C.
)=C.
M4) 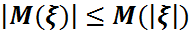 .
.
M5)Егер 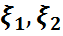 өзара тәуелсіз болса,онда М(
өзара тәуелсіз болса,онда М(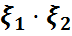 )=M(
)=M(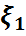 )
)  M(
M(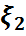 ).
).
M6) 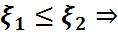 M(
M(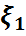 )
) 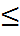 M(
M(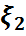 ).
).
M7)Коши-Буряковский теңсіздігі 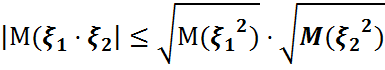 .
.
Үзіліссіз кездейсоқ шаманың дисперсиясы, орта квадраттық ауытқуы. Қасиеттері.
Анықтама: Х кездейсоқ шамасы қабылдайтын мәндер шекті немесе шексіз интервалдың барлық мәндерін қабылдаса ол үзіліссіз кездейсоқ шама деп аталады.
Анықтама: X: Ω→R кездейсоқ шамасының дисперсиясы деп D(X)≡Var(X)=M(X-M(X))2 санын айтады.
Орташа квадраттық ауытқуы 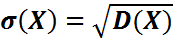 формуласымен табылады.
формуласымен табылады.
Қасиеттері: 1.Егер Х=c болса, онда D(X)=0.
2. D(X) = M(X2) – M2(X)
3. D(a X+b) = a2 D(X)
4. D(a X1 + b X2)=a2 D(X1) + b2 D(X2) + 2ав M((X1 – M(X1)) (X2 – M(X2))).
Дербес жағдай: X1, X2 тәуелсіз болса, онда D(a X1 + b X2) = a2 D(X1) + b2 D(X2).
| 32.Сенімділік интервалы. а) таңдама, нүктелі және интервалды бағалар б) Математикалық күтімі белгілі нормаль үлестірімнен алынған таңдама бойынша белгісіз дисперсияға сенімділік интервалын құру. в)Хи-квадрат үлестірімнің келіп шығуы және қолданылуы. |
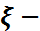 бақыланатын кездейсоқ шамасы қалыпты үлестірілгендігі,оның
бақыланатын кездейсоқ шамасы қалыпты үлестірілгендігі,оның 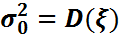 – дисперсиясы белгілі болсын.a=M(
– дисперсиясы белгілі болсын.a=M(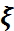 ) – математикалық күтімі белгісіз
) – математикалық күтімі белгісіз 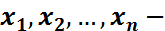
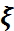 -ден алынған таңдама.Демек,
-ден алынған таңдама.Демек, 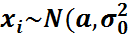 ),(
),(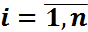 )
)
a үшін баға  =
= 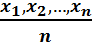 болатын.
болатын. 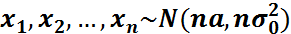 болатыны белгілі.Олай болса
болатыны белгілі.Олай болса 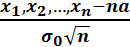
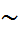 N(0,1).Бұдан алымы мен бөлімін n-ге бөлсек
N(0,1).Бұдан алымы мен бөлімін n-ге бөлсек 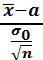
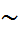 N(0,1)
N(0,1)
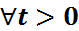 үшін P
үшін P 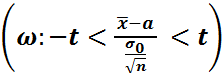 =
= 
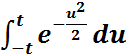 болады.
болады.
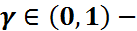 саны берілсін(сенімділік деңгейі,басқаша айтса,қажет ықтималдық) Содан
саны берілсін(сенімділік деңгейі,басқаша айтса,қажет ықтималдық) Содан 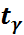 санын
санын 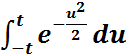 =
= 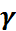 , (немесе
, (немесе 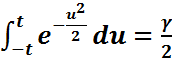 ) болатындай етіп таңдайды.Сонда
) болатындай етіп таңдайды.Сонда
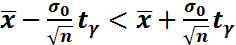 интервалы белгісіз а үшін маңыздылық
интервалы белгісіз а үшін маңыздылық 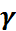 болатын сенімділік интервалы деп аталады.Бұл мысалда
болатын сенімділік интервалы деп аталады.Бұл мысалда  - a үшін нүктелі баға,ал (
- a үшін нүктелі баға,ал (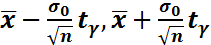 ) – a үшін интералды баға.
) – a үшін интералды баға.
Дата добавления: 2016-01-03; просмотров: 1; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
