В)Жеке мәндерінің ықтималдығын үлестірім функциясы арқылы өрнектеу
ξ: Ω → X = {  ,
, 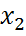 ,…} ⊂ R кездейсоқ шамасының мүмкін олатын жиыны ақырлы немесе саналымды болса, ξ дискрет кездейсоқ шама деп аталады.
,…} ⊂ R кездейсоқ шамасының мүмкін олатын жиыны ақырлы немесе саналымды болса, ξ дискрет кездейсоқ шама деп аталады.
ξ кездейсоқ шамасының үлестірім функциясы 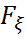 (x) дискретті үлестірім функциясы болсын.Онда
(x) дискретті үлестірім функциясы болсын.Онда
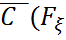 )={
)={  ,
, 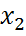 ,…}, мұндағы
,…}, мұндағы 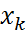 нүктелері үшін
нүктелері үшін 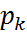 =
=  =P{
=P{ 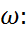 ξ(
ξ(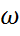 ) =
) = 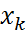 }=
}= 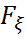 (x)-
(x)- 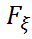 (x-0), яғни
(x-0), яғни  үлестірім заңы (ықтималдық өлшемі)
үлестірім заңы (ықтималдық өлшемі) 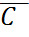
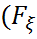 ) жиынының нүктелерінде шоғырланған және
) жиынының нүктелерінде шоғырланған және 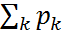 =1. Мұндай кездейсоқ шама үшін оның кез келген B ϵ β(R) борелдік жиынына түсу ықтималдығы
=1. Мұндай кездейсоқ шама үшін оның кез келген B ϵ β(R) борелдік жиынына түсу ықтималдығы
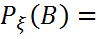 P{ ξ ϵ B }=
P{ ξ ϵ B }=  =
= 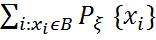 =
= 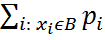 . (1)
. (1)
Жеке мәндер ықтималдығы арқылы үлестірім функциясының дербес жағдайын аламыз:
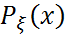 =
= 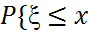 }=
}= 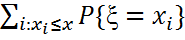 =
= 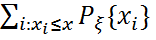 =
=
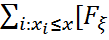 (
(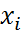 ) -
) - 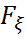 (
(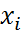 -0)]
-0)]
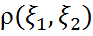 =
= 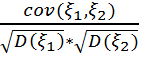 қатынасымен анықталған
қатынасымен анықталған 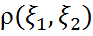 шамасы
шамасы 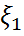 және
және 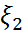 кездейсоқ шамаларының корреляция коэффициенті деп аталады.
кездейсоқ шамаларының корреляция коэффициенті деп аталады.
Қасиеттері:
1) 
2) -1 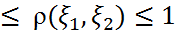
| 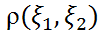 |=1 болуы үшін
|=1 болуы үшін 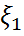 мен
мен 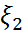 өзара сызықты тәуелді болуы қажетті және жеткілікті.
өзара сызықты тәуелді болуы қажетті және жеткілікті.
1) 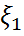 мен
мен 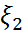 тәуелсіз болса, онда
тәуелсіз болса, онда 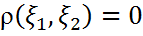
Бұл қасиеттерден мынадай тұжырым алуға болады: корреляциялық коэффициент екі кездейсоқ шаманың тәуелділігінің өлшеуіші болып табаылады. Корреляциялық коэффициент +1 немесе -1-ге жақын болса, олардың арасындағы тәуелділік күшті деген сөз. Ал корреляциялық коэффициент 0-ге жақын болса, онда олардың арасындағы тәуелділік әлсіз.
|
|
|
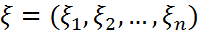 кездейсоқ жол-векторының компененталары болатын
кездейсоқ жол-векторының компененталары болатын 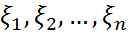 кездейсоқ шамалары үшін
кездейсоқ шамалары үшін 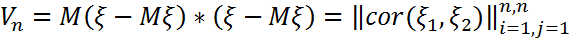
матрицасы олардың корреляциялық матрицасы деп аталады.
| 5. | Кездейсоқ шама. а) Кездейсоқ шама анықтамасы. б) Үлестірімі заңы, үлестірім функциясы және оның негізгі төрт қасиеті. в) Үлестірім функциясының қосымша қасиеттері |
Анықтама:  - ықтималдық кеңістігі берілсін.
- ықтималдық кеңістігі берілсін. 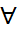 I(I
I(I 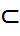 R) аралығы үшін
R) аралығы үшін 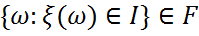 шартын қанағаттандыратын
шартын қанағаттандыратын 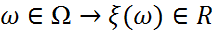 функциясын кездейсоқ шама дейді.
функциясын кездейсоқ шама дейді.
Үлестірім 𝜉:Ω  Rкездейсоқ шамасының үлестірімі деп
Rкездейсоқ шамасының үлестірімі деп 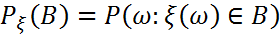 (1) түріндегі ықтималдықтар жиынын айтады. Мұндағы B
(1) түріндегі ықтималдықтар жиынын айтады. Мұндағы B  R- аралықтар және олардың ақырлы, саналымды бірігулері түріндегі санды жиындар. Кездейсоқ шамасының үлестірімі оның қай аралықта мән қабылдау ықтималдығы қандай екенін көрсетеді.
R- аралықтар және олардың ақырлы, саналымды бірігулері түріндегі санды жиындар. Кездейсоқ шамасының үлестірімі оның қай аралықта мән қабылдау ықтималдығы қандай екенін көрсетеді.
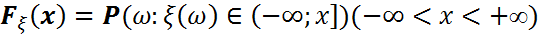 (2) функциясын 𝜉 кездейсоқ шамасының үлестірім функциясы дейді. (1) –ді ескерсек (2)-ні былай да жазуға болады:
(2) функциясын 𝜉 кездейсоқ шамасының үлестірім функциясы дейді. (1) –ді ескерсек (2)-ні былай да жазуға болады: 
Қaсиетері: F1) 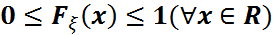
F2) 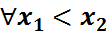 үшін
үшін 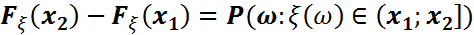 болады. Бұдан
болады. Бұдан 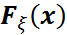 функциясы кемімейтін функция екені шығады.
функциясы кемімейтін функция екені шығады.
|
|
|
F3) әрбір 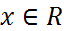 нүктесінде оң жақты үзіліссіз:
нүктесінде оң жақты үзіліссіз: 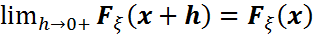
F4) 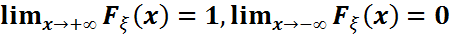
Дәлелдеуі:F2): 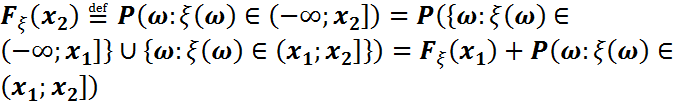 Бұдан F2) дәлелденеді.
Бұдан F2) дәлелденеді.
| 6. | Ковариация а) анықтамасы және дискрет жағдайда есептеу формуласы б) абсолют үзіліссіз жағдайда есептеу формуласы в) қасиеттері |
Коварация екі кездейсоқ шама үшін анықталады.
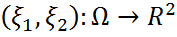 кездейсоқ вектор.
кездейсоқ вектор.
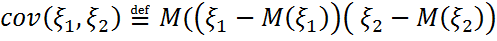
Коваряция қасиеттері
1) 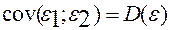
2) 
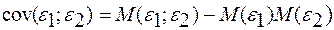
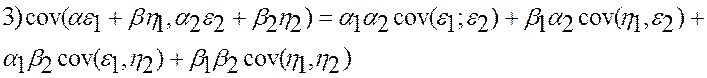 4)
4) 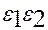 тәуелсіз болса онда
тәуелсіз болса онда 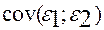 =0
=0
5) | 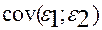 |≤
|≤ 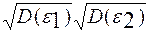 бұл жерде (
бұл жерде (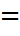 )орындалуы үшін
)орындалуы үшін 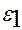 мен
мен 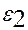 сызықты тәуелді болуы қажетті және жеткілікті.Дәлелденуі жақшаларды ашу және математикалық күтімнің сызықты қасиеттеріне сүйенеді.
сызықты тәуелді болуы қажетті және жеткілікті.Дәлелденуі жақшаларды ашу және математикалық күтімнің сызықты қасиеттеріне сүйенеді.
| 7. | Ықтималдық кеңістігі а)Элментар оқиға. Элементар оқиғалар кеңістігі. б)Оқиғалар және оқиғаларға амалдар қолдану. в)Оқиға жиілігі, оның қасиеттері. Ықтималдық аксиомалары және олардың салдарлары Мысалдары. |
Әрбір кездейсоқ нәтижелі сынақтың математикалық моделі ретінде оған сәйкес 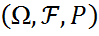 үштігі болады. Бұл үштік сол сынақтың ықтималдық кеңістігі деп аталады.Енді осы үштіктің компоненттеріне жеке-жеке тоқталайық.I)Элементар оқиғалар кеңістігі.
үштігі болады. Бұл үштік сол сынақтың ықтималдық кеңістігі деп аталады.Енді осы үштіктің компоненттеріне жеке-жеке тоқталайық.I)Элементар оқиғалар кеңістігі.  элементар оқиға.Сынақтың әрбір мүмкін болатын қарапайым нәтижесін элементар оқиға д.а және
элементар оқиға.Сынақтың әрбір мүмкін болатын қарапайым нәтижесін элементар оқиға д.а және 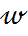 н/е
н/е 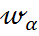 деп белгілейді.II)Оқиға ұғымы.
деп белгілейді.II)Оқиға ұғымы.  -ның қандай да бір жиыншасы-ол оқиға.III)Жиілік және оның қасиеттері.Статистикалық орнықтылық.Ықтималдық ұғымы.Қандай да бір сынақ берілсін ж/е
-ның қандай да бір жиыншасы-ол оқиға.III)Жиілік және оның қасиеттері.Статистикалық орнықтылық.Ықтималдық ұғымы.Қандай да бір сынақ берілсін ж/е 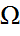 оның Э.К.О болсын.
оның Э.К.О болсын. 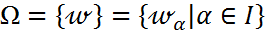 - ал
- ал 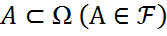 -қандай да бір оқиға болсын.Сынақ n рет қайталансын.
-қандай да бір оқиға болсын.Сынақ n рет қайталансын. 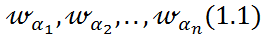 Бұл тізбекке сәйкес A оқиғасының жиілігі деп
Бұл тізбекке сәйкес A оқиғасының жиілігі деп 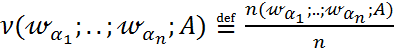 ;
;
|
|
|
Жиіліктің қасиеттері: 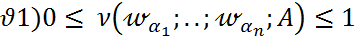
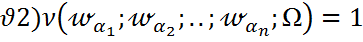
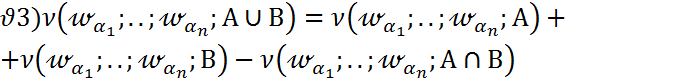
Егер 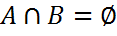 болса:
болса:
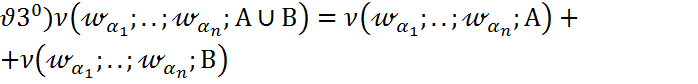
Ықтималдық аксиомалары.Сынақ берілсін.  -оның Э.К.О.,
-оның Э.К.О., 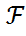 -оқиғалар,
-оқиғалар, 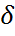 -алгебрасы болсын.Ықтималдық аксиомалары:
-алгебрасы болсын.Ықтималдық аксиомалары: 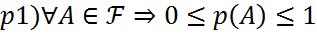
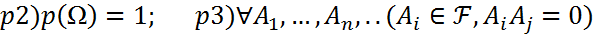 Үйлесімсіз оқиғалар тізбегі үшін
Үйлесімсіз оқиғалар тізбегі үшін 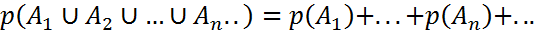 теңдігі орындалса,жоғарыдағы ұасиеттерге ие болатын
теңдігі орындалса,жоғарыдағы ұасиеттерге ие болатын 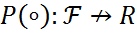
| 8.Екі өлшемді нормаль (гаустік) үлестірім. | |
Нормаль (гаустік) үлестірім функциясы
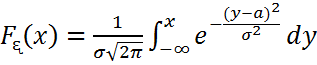 (1)
(1)
қатынасымен берілетін кездейсоқ шама ретінде анықталады, мұндағы параметрлер 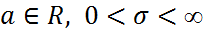
(1) формуласымен анықталған 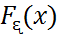 функциясы -үлестірім функциясы болады.
функциясы -үлестірім функциясы болады.
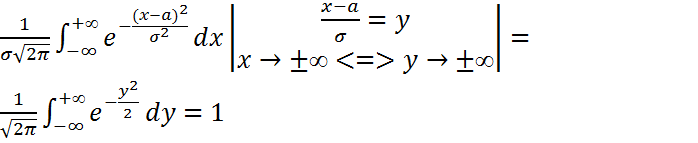
Сонымен нормаль кездейсоқ шаманың үлестірім функциясы екі a және 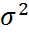 (яғни
(яғни 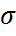 ) параметрлеріне тәуелді.
) параметрлеріне тәуелді.
|
|
|
Айталық V= 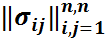 қандай да бір қатаң оң нақтыланған және симметриялы n
қандай да бір қатаң оң нақтыланған және симметриялы n  n – матрица болсын:
n – матрица болсын: 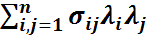 >0,
>0, 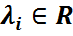 ,
, 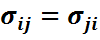 (i,j=1,…,n). Онда кері матрицасы А=
(i,j=1,…,n). Онда кері матрицасы А= 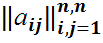 =
= 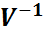 бар және V матрицасы (detV>0) үшін
бар және V матрицасы (detV>0) үшін
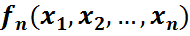 =
= 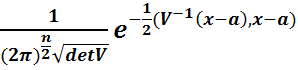 (1)
(1)
Функциясы анықталған болады, мұндағы x=(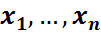 )
) 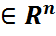 , x,y
, x,y  үшін (x,y)=
үшін (x,y)=  . (1)-формуламен анықталған
. (1)-формуламен анықталған 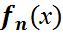 функциясы көп өлшемді үлестірім тығыздығы болады. Бұл үлестірім тығыздығын n -өлшемді ерекше емес нормаль (гаустық) үлестірімнің үлестірім тығыздығы деп аталады.
функциясы көп өлшемді үлестірім тығыздығы болады. Бұл үлестірім тығыздығын n -өлшемді ерекше емес нормаль (гаустық) үлестірімнің үлестірім тығыздығы деп аталады.
| 9.Геометориялық ықтималдықтар. а) Геометриялық ықтималдық формуласының жалпы түрі. Мысалдар. б) Кездесу туралы есеп. |
Геометриялық ықтималдық дегеніміз 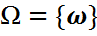 жиыны
жиыны 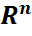 - n өлшемді Евклид кеғістігінің қандай да бір шенелген ішкі жиыны болсын.
- n өлшемді Евклид кеғістігінің қандай да бір шенелген ішкі жиыны болсын. 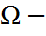 ның “көлемі” (n=1 үшін – ұзындығы, n=2 үшін – ауданы, n=3 үшін – әдеттегі көлемі т.с.с) бар болатын ішкі оқиғалар жүйесін белгілелік те, кез-келген A
ның “көлемі” (n=1 үшін – ұзындығы, n=2 үшін – ауданы, n=3 үшін – әдеттегі көлемі т.с.с) бар болатын ішкі оқиғалар жүйесін белгілелік те, кез-келген A 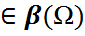 оқиғасы үшін оның ықтималдығын
оқиғасы үшін оның ықтималдығын
P(A)= 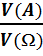 (1) қатынасымен анықтаймыз, мұндағы V(A) – A жиынының “көлемі”.
(1) қатынасымен анықтаймыз, мұндағы V(A) – A жиынының “көлемі”.
Ықтималдықты осылайша (1) – формуламен анықтау ықтималдықтың геометриялық анықтамасы деп аталады.
Бұл құрастырылған модельді Ω аймағына нүктені кездейсоқ лақтырудан тұратын тәжірбиенің моделі ретінде қарастыруға болады.
Кездесу туралы есеп. Екі адам, А мен В, [0,T] уақыт аралығында бір-бірімен кездесуге уәделескен. Егер уәделі жерге A(B) бірінші келсе, ол В-ны (A-ны) 𝛥t уақыт бойы күтіп, ол осы уақыт аралығында келмесе кетіп қалатын болып келіскен.Екеуінің кездесу ықтималдығы неге тең?
Шешуі. Сигнал- А, қабылдағыш- В. Ендеше кездесу ықтималдығы былай анықталады егер Т=1 сағат, t=15 минут, 𝛥=20 минут болса, онда p= 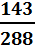 . Егер Т=1 сағат, t= 𝛥=15 минут болса, онда p=
. Егер Т=1 сағат, t= 𝛥=15 минут болса, онда p= 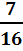 .
.
| 10. | Геометриялық үлестірім а) анықтамасы және оған әкелетін мысал б) оның математикалық күтіміне формула қорыту в)оның дисперсиясына формула қорыту. |
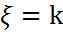 дискретті кездейсоқ шамасы геометриялық үлестірім болады, егер ол 1, 2,... (шексіз мәндер) мәндерін келесі ықтималдылықпен қабылдайтын болса:
дискретті кездейсоқ шамасы геометриялық үлестірім болады, егер ол 1, 2,... (шексіз мәндер) мәндерін келесі ықтималдылықпен қабылдайтын болса:
|
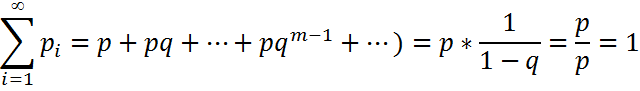
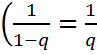 сияқты геометриялық қатар қосындысы
сияқты геометриялық қатар қосындысы 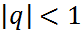
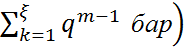 .
.
Математикалық күтімі: 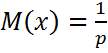
Ал Дисперсиясы D(x)= 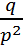 мұнда
мұнда 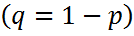

| 11. | Ықтималдықтарды қосу формуласы а) Екі оқиға үшін дәлелдеу б) Үш оқиға үшін дәлелдеу в) n оқиға үшін дәлелдеу |
Шартты ықт.формуласыннан P(A\B) =  =>
=>
P(AB) = P(B) P(A\B) немесе P(AB) = P(A) P(B\A)
Дәлелдеуі.
P(A\B)=P(A)+P(B)-P(AB) (1)
A=(A\B) 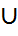 AB. Онда P3) бойынша P(A)=P(A\B)+P(AB) болады,осыдан (1) шығады. Енді (1) былай дәлелденеді: A
AB. Онда P3) бойынша P(A)=P(A\B)+P(AB) болады,осыдан (1) шығады. Енді (1) былай дәлелденеді: A 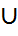 B=(A\B)
B=(A\B) 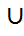 B, тағыда P3) бойынша
B, тағыда P3) бойынша
P(A 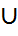 B)=P(A\B)+P(B)=P(A)-P(AB)+P(B)
B)=P(A\B)+P(B)=P(A)-P(AB)+P(B)
Үш оқиға үшін қосу формуласы:
P(A 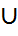 B
B 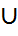 C)=P(A)+P(B)+P(C)-P(AC)-P(AB)-P(BC)+P(ABC) болатыны (1)-ден шығады.
C)=P(A)+P(B)+P(C)-P(AC)-P(AB)-P(BC)+P(ABC) болатыны (1)-ден шығады.
n-oқиға үшін: P(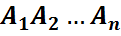 )=P(
)=P(

Мат.индукция: 1): n=2: P 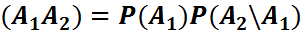 ақиқат
ақиқат
2)n=m-1 үшін:
P(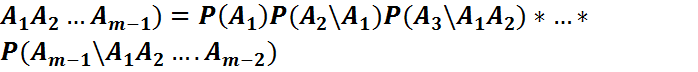 дұрыс деп ұйғарайық
дұрыс деп ұйғарайық
3)n=m үшін:
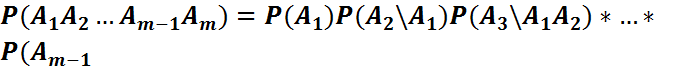 \
\ 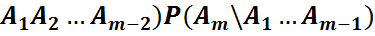
| 12. | Гипергеометриялық үлестірім а) анықтамасы және қолданылу мысалы б) оның математикалық күтімін есептеуге қысқаша формула қорыту в)оның дисперсиясын есептеуге қысқаша формула қорыту. |
Дискретті ξ кездейсоқ шамасының гипергеометриялық үлестірімі болады, егер оның k=0,1,2,3,....,m) мәнінде
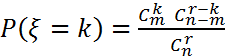 ықтималдықтары бар болады.
ықтималдықтары бар болады.
Алдыңғы формуладан мынандай қатынас шығады:
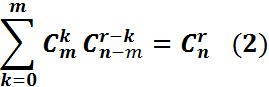
Гипергеометриялық үлестірімнің математикалық күтімі:
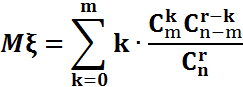
Қосынды ішіндегі  –ды
–ды 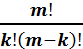 түрінде жазып, сәйкес қысқартуларды орындасақ, мынаны аламыз:
түрінде жазып, сәйкес қысқартуларды орындасақ, мынаны аламыз:
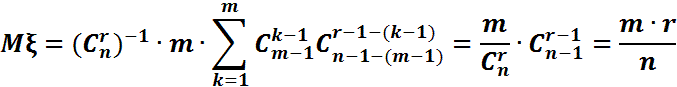
Теорема. n,m,r параметрімен үлестірілген ξ кездейсоқ шамасының гипергеометриялық үлестірімінің математикалық күтімі: 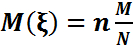
Ал дисперсиясы: 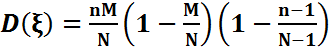 тең.
тең.
| 13. | Күрделі функция түріндегі кездейсоқ шамалар а)Көп айнымалылы сан мәнді борель функциясы мен кездейсоқ вектор композициясы түріндегі кездейсоқ шама үлестірімі б)Екі тәуелсіз кездейсоқ шаманың қосындысының үлестірімі. Үйірткі (свертка) формуласы. в) Көп айнымалылы сан мәнді борель функциясы мен кездейсоқ вектор композициясы түріндегі кездейсоқ шаманың математикалық күтімі |
Теорема: 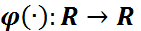 және кез келген
және кез келген  үшін
үшін 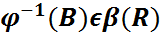 қанағаттандыратын функция, ал
қанағаттандыратын функция, ал 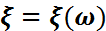 – кездейсоқ шама болса, онда
– кездейсоқ шама болса, онда 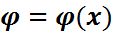 – борельдік функция болады. Онда
– борельдік функция болады. Онда 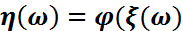 ) – кездейсоқ шама.
) – кездейсоқ шама.
Дәлелдеу: Кез келген  үшін:
үшін:
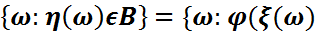 )
) 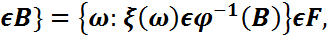
себебі 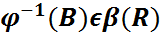 , ал 𝜉 – кездейсоқ шама.(дәлелденді)
, ал 𝜉 – кездейсоқ шама.(дәлелденді)
Үзіліссіз және бөлікті үзіліссіз функциялар борельдік функциялар класына жатады.
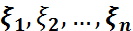 –
–  ықтималдық кеңістігінде анықталған кездейсоқ шамалар болсын. Әрбір
ықтималдық кеңістігінде анықталған кездейсоқ шамалар болсын. Әрбір 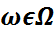 элементар оқиғасына бұл кездейсоқ шамалар
элементар оқиғасына бұл кездейсоқ шамалар 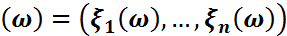 векторын сәйкес қояды. Бұл- кездейсоқ вектор деп аталады.
векторын сәйкес қояды. Бұл- кездейсоқ вектор деп аталады.
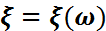 кездейсоқ векторы арқылы берілген
кездейсоқ векторы арқылы берілген 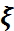 :
: 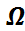 →
→ 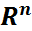 бейнелеуі өлшенетін бейнелеу: кез-келген
бейнелеуі өлшенетін бейнелеу: кез-келген 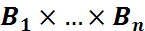 =B∈β(
=B∈β(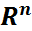 ) n өлшемді борелдік жиыны үшін
) n өлшемді борелдік жиыны үшін
 ={ω:(
={ω:(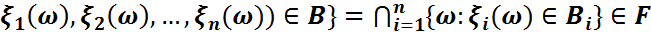 (1)
(1)
Ендеше әрбір 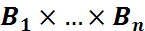 =B∈β(
=B∈β(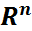 ) n өлшемді борелдік жиыны үшін
) n өлшемді борелдік жиыны үшін 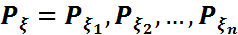 функциясын былайша анықтай аламыз:
функциясын былайша анықтай аламыз:
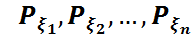 (
(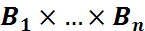 )=
)= 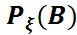 =P{
=P{ 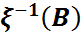 }=
}=
=P {ω: 
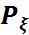 -(
-(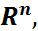 β(
β(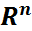 )) кеңістігінде анықталған ықтималдықтық функция (өлшем) болатынын бір өлшемді жағдайдағы секілді дәлелдеуге болады. Сонымен, кез келген
)) кеңістігінде анықталған ықтималдықтық функция (өлшем) болатынын бір өлшемді жағдайдағы секілді дәлелдеуге болады. Сонымен, кез келген 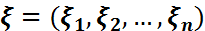 көп өлшемді кездейсоқ шамасы жаңа, (
көп өлшемді кездейсоқ шамасы жаңа, (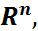 β(
β(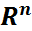 ),
), 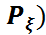 ықтималдық кеңістігін пайда қылады. Бұл ықтималдық кеңістігі
ықтималдық кеңістігін пайда қылады. Бұл ықтималдық кеңістігі 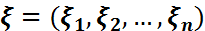 көр (n) өлшемді 𝜉 кездейсоқ шамасы (кездейсоқ векторы) арқылы пайда болған ықтималдық кеңістігі деп, ал
көр (n) өлшемді 𝜉 кездейсоқ шамасы (кездейсоқ векторы) арқылы пайда болған ықтималдық кеңістігі деп, ал 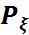 ықтималдықтық өлшемі көп өлшемді 𝜉 кездейсоқ шамасының үлестірім заңы деп аталады.
ықтималдықтық өлшемі көп өлшемді 𝜉 кездейсоқ шамасының үлестірім заңы деп аталады.
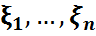 -абсолютті үзіліссіз кездейсоқ шамалар,
-абсолютті үзіліссіз кездейсоқ шамалар, 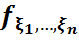 (
(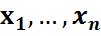 )=f(
)=f(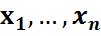 )-олардың бірлескен үлестірім тығыздығы болсын.η=
)-олардың бірлескен үлестірім тығыздығы болсын.η= 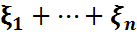 кездейсоқ шамасының абсолютті үзіліссіз кездейсоқ шама болатынын көрсетелік және оның үлестірім тығыздығының айқын түрін табайық
кездейсоқ шамасының абсолютті үзіліссіз кездейсоқ шама болатынын көрсетелік және оның үлестірім тығыздығының айқын түрін табайық
Анықтама бойынша 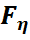 (x)=P{η
(x)=P{η 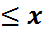 }=P{
}=P{ 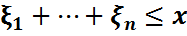 }=
}=  d
d 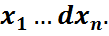
Айталық,n=2 болсын. Бұл жағдайда 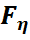 (x)=
(x)=  d
d 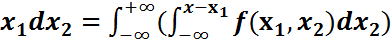 d
d 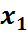 =
=  d
d 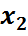
Жаңа айнымалыларды енгізіп интегралдарды түрлендірсек онда 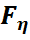 (x)=
(x)= 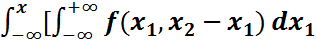 ]d
]d 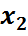 =
= 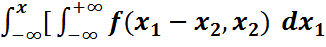 ]
] 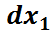
оның тығыздығы
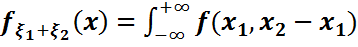 d
d 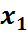 =
=  (
(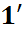 )
)
Формулаларымен анықталатындығы көрсетіледі.
Егер қосымша 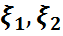 тәуелсіз кездейсоқ шамалар, ал
тәуелсіз кездейсоқ шамалар, ал  ,
, 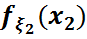 олардың үлестірім тығыздығы боса, онда
олардың үлестірім тығыздығы боса, онда 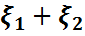 тығыздығы
тығыздығы
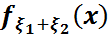 =
= 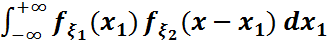 =
= 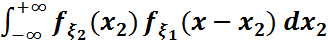 (1)
(1)
Формуласымен анықталатынын аламыз.
Соңғы формула композиция формуласы немесе үйірткі формуласы деп аталады. Композиция формуласын әдетте  түрінде жазады.
түрінде жазады.
| 14.Параметрлерді бағалау есебі. а) Параметрлерді бағалау есебінің қойылуы б) Нүктелік баға. б) Ығыспаған баға, тиянақты баға және тиімді баға. Мысалдары |
Сәйкестендіріліп терілген x1,x2,...,xn үлестіру функциясы белгісіз 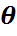 параметрге байланысты болсын делік.
параметрге байланысты болсын делік.
p(xk<x)=F(x,  )
)
Статистикалық бағалаудың бір санмен анықталған түрін нүктелік бағалау деп аталады.
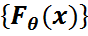 ө=ї= үлестірім функциялар жиынтығы, мұндағы
ө=ї= үлестірім функциялар жиынтығы, мұндағы 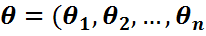 )
) 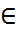 ї
ї 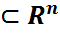 ,
, 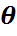 -белгісіз параметр деп аталады, ал ї-белгісіз параметрлер жиыны
-белгісіз параметр деп аталады, ал ї-белгісіз параметрлер жиыны
Есептің қойылуы: Қандайда бір 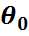 үшін сәйкес
үшін сәйкес 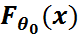 үлестірім функциясы
үлестірім функциясы 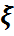 - функциясы болып табылады, яғни
- функциясы болып табылады, яғни  (x)=
(x)= 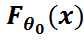 . Мәселе- сол
. Мәселе- сол 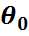 -ді таңдамадан пайдаланып жуықтап табу керек.
-ді таңдамадан пайдаланып жуықтап табу керек.
Қойылған есепті шешу үшін 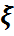 -ден алынған x1(
-ден алынған x1(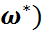 ,x2
,x2 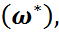 ..., xn
..., xn 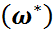 пайдаланамыз.
пайдаланамыз. 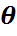 - белгісіз параметрінің мағынасына қарай
- белгісіз параметрінің мағынасына қарай
 ї
ї
функциясын құрады және ол арқылы мына функцияға келеді
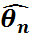 (
(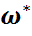 )=
)= 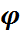 (
(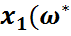 ),
), 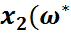 ),...,
),..., 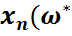 )): Ώ*
)): Ώ*  ї
ї
Бұл функция 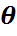 -белгісіз параметрінің бағасы деп аталады.
-белгісіз параметрінің бағасы деп аталады.
ξ кездейсоқ шамасының үлестірім функциясы B ϵ β(R) борелдік жиынына түсу ықтималдығы
Егер ξ кездейсоқ шамасының Дискретті ықтималдық кеңістігінде анықталған кез келген сандық мәнді функция дискретті кездейсоқ шама болады, себебі Ω= { :
шарты орындалса, онда
санын айтады. Қасиеттері (Математикалық күтім) ( M1) M M2) Сызықты қасиеті М3) Егер
M4) M5) Егер
M6) M7) Коши-Буряковский теңсіздігі
|
А) Таңдама ұғымы
Дата добавления: 2016-01-03; просмотров: 1; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!


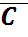
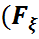 )={
)={ 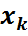 нүктелері үшін
нүктелері үшін 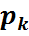 =
= 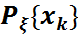 =P{ ξ =
=P{ ξ = 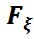 (x-0), яғни
(x-0), яғни 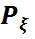 үлестірім заңы (ықтималдық өлшемі)
үлестірім заңы (ықтималдық өлшемі) 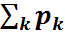 =1. Мұндай кездейсоқ шама үшін оның кез келген
=1. Мұндай кездейсоқ шама үшін оның кез келген P{ ξ ϵ B }=
P{ ξ ϵ B }= 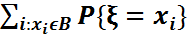 =
= 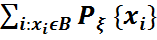 =
= 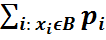 . (1) Бұдан
. (1) Бұдан 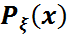 =
=  }=
}= 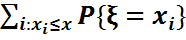 =
= 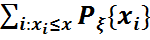 =
= 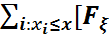 (
( ) -
) - 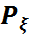 үлестірім заңы (1)-қатынаспен анықталса, онда мұндай кездейсоқ шаманы дискретті кездейсоқ шама деп атаймыз. Басқаша айтқанда, дискретті кездейсоқ шама дегеніміз қабылдайтын мәндерінің жиыны ақырлы не саналымды жиын болатын кездейсоқ шама: ξ: Ω → X = {
үлестірім заңы (1)-қатынаспен анықталса, онда мұндай кездейсоқ шаманы дискретті кездейсоқ шама деп атаймыз. Басқаша айтқанда, дискретті кездейсоқ шама дегеніміз қабылдайтын мәндерінің жиыны ақырлы не саналымды жиын болатын кездейсоқ шама: ξ: Ω → X = { 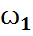 ,
, 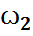 ,…}, үшін F={A: A⊂Ω}, ξ:Ω→X={ξ
,…}, үшін F={A: A⊂Ω}, ξ:Ω→X={ξ 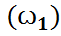 , ξ
, ξ 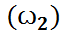 ,… } және кез келген B ϵ β(R) борелдік жиыны үшін
,… } және кез келген B ϵ β(R) борелдік жиыны үшін 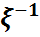 (B)={ꙍ: ξ(ꙍ)ϵB} =
(B)={ꙍ: ξ(ꙍ)ϵB} = 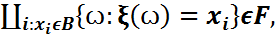
 {
{ 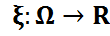 дискрет кездейсоқ шама беріліп,
дискрет кездейсоқ шама беріліп,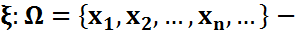 мәндер жиыны,
мәндер жиыны,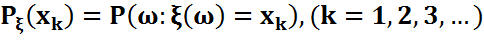 -үлестірімі белгілі болсын. Егер
-үлестірімі белгілі болсын. Егер
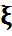 кездейсоқ шаманың ақырлы математикалық күтімі бар дейді. Оның математикалық күтімі деп
кездейсоқ шаманың ақырлы математикалық күтімі бар дейді. Оның математикалық күтімі деп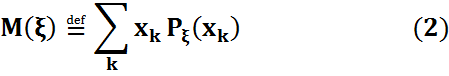
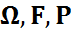 )- ықтималдық кеңістікте
)- ықтималдық кеңістікте 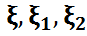 кездейсоқ шамалары беріліп, олардың ақырлы математикалық күтімдері бар болсын.
кездейсоқ шамалары беріліп, олардың ақырлы математикалық күтімдері бар болсын.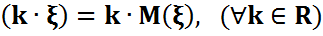
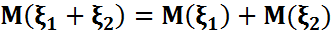
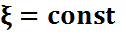 кездейсоқ шама болса, ол дегеніміз
кездейсоқ шама болса, ол дегеніміз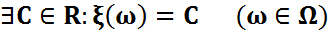 , онда
, онда 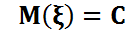
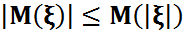
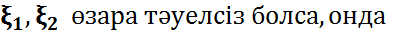
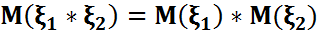
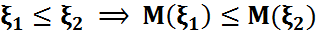
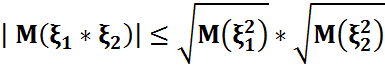 16,Сенімділік интервалы
16,Сенімділік интервалы