Преобразование Ватсона. Ползущие волны

Знакомство с ползущими волнами и связанным с ними преоб­разованием Ватсона начнём с рассеивателей в форме кругового цилиндра, а затем обобщим эти понятия на тела другой формы.

Давление в волне, рассеянной идеальным цилиндром, (4.27) удобно представить в виде ряда по экспонентам, а не по косину­сам:

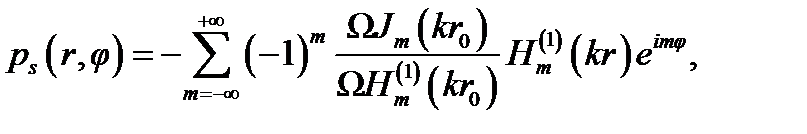(4.33)

где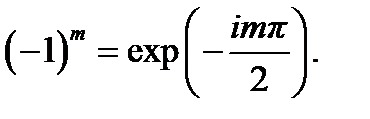

Дифрагированное давление p_Σ = p_i + p_s будет иметь вид

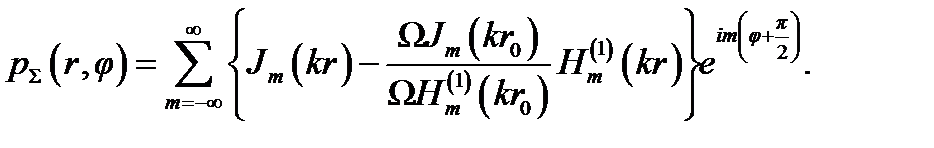(4.34)

Анализ ряда (4.34) показывает, что его члены очень медленно меняются по модулю с ростом т вплоть до т , при этом их фаза изменяется от члена к члену весьма сложным образом. Только при т > kr₀ члены начинают быстро убывать с ростом т (быстрее, чем экспонента). Этим и определяется то обстоятельство, что хотя ряды и сходятся при всех kr_o, но, поскольку число членов ряда, которые необходимо учитывать, имеет величину порядка kr_o, пользоваться этими рядами для подсчёта при больших kr_o не­целесообразно. Таким образом, при kr_o следует искать другие представления р_Σ, одним из которых и является преобразование ряда, предложенное Ватсоном и заключающееся в том, что бес­конечный ряд вида

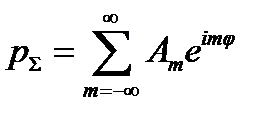(4.35)

преобразуется в интеграл

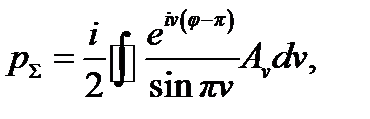(4.36)

причём контур интегрирования на комплексной плоскости v охватывает вещественную ось, как показано на рис. 4.12. Действительно, если функция A_v не имеет полюсов на вещественной оси, интеграл (4.36) в силу теоремы Коши равен сумме (4.35), так как множитель при A_v имеет в точках v = т (где т — целое число) полюсы первого порядка с вычетами

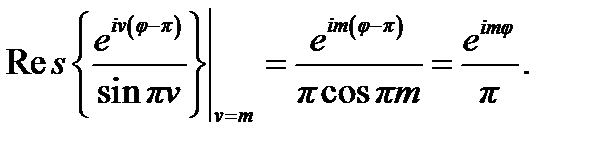(4.37)

Если к тому же коэффициент A_v является чётной функцией v (т. е. если 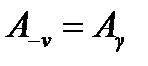), то из выражения (4.36) получим (заменив на части контура интегрирования, лежащей в нижней полуплоскости, переменную v на —v)

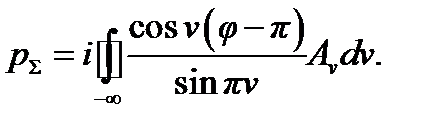(4.38)

 

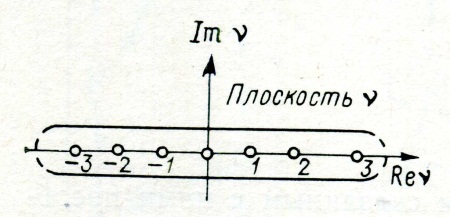Рис. 4.12. Контур интегрирования

на ком­плексной плоскости индекса v.

В качестве контура интегриро-вания здесь следует взять пря-мую, параллельную вещест-венной оси и лежащую в верх-ней полуплоскости (или вести интегрирование по самой ве-щественной оси, обходя целочисленные значения v). Преимущество, даваемое преобразованием Ватсона, заключается в возможности деформирования контура интегрирования.

Применим преобразование Ватсона к ряду(4.34), в котором A_v имеет вид

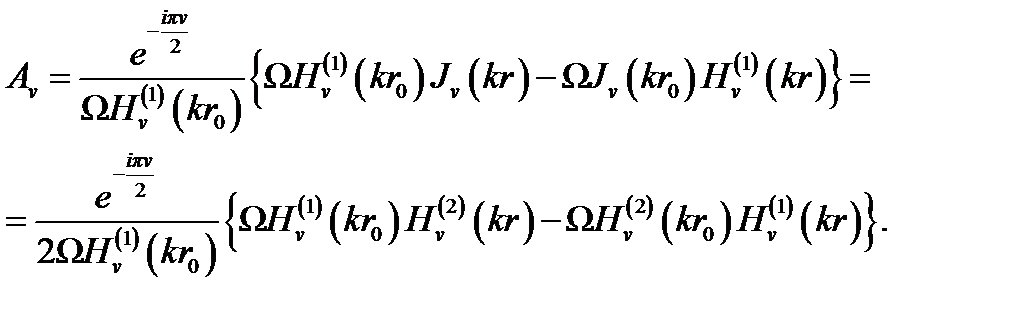(4.39)

Для цилиндрических функций Ханкеля с большим (положительным вещественным) аргументом и произвольным (комплексным) индексом справедливы асимптотические выражения, связывающие значения функций в левой и правой полуплоскостях:

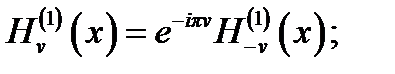
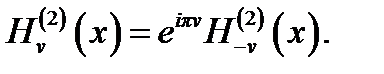(4.40)

В силу (4.40) A_v является чётной функцией v, так что можно применить формулу (4.38). Деформируем теперь контур интегрирования в петлю, охватывающую корни v_s уравнения

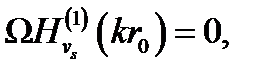(4.41)

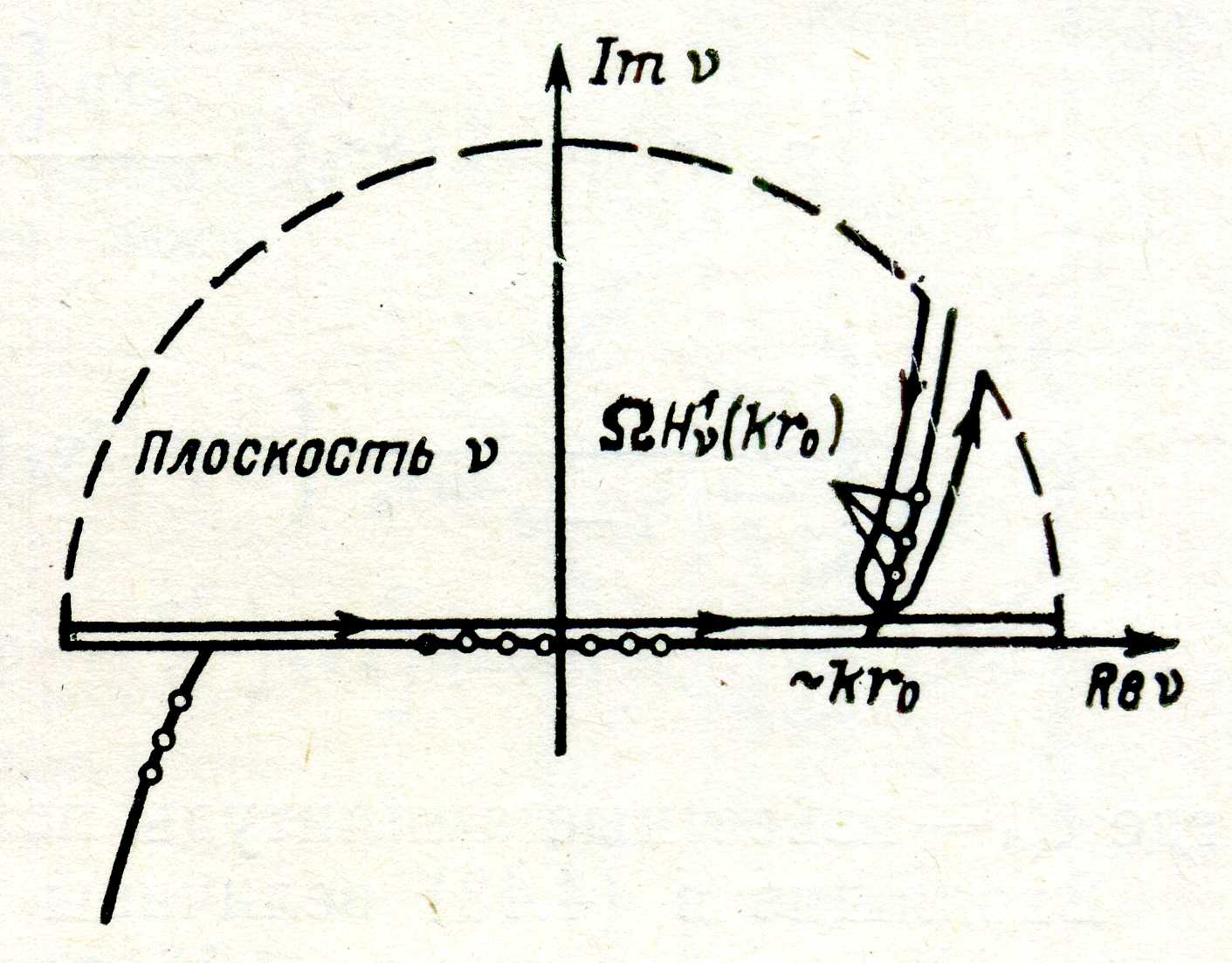Рис. 4.13. Деформированный контур интегрирования

которые лежат в правом квадранте плоскости v, и полуокружность бесконечно большого радиуса в верхней полуплоскости (рис. 4.13). Зная поведение цилиндрических функций в бесконечности на пло­скости v (рис. 4.14), можно показать, что подынтегральная функ­ция в интеграле (4.38) [где A_v выражается формулой (4.39)] всюду, за исключением окрестности нулей функции 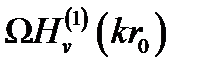, убы­вает быстрее, чем экспонента. Точки v_s являются полюсами пер­вого порядка для A_v; таким образом, можно представить рассмат­риваемый интеграл как сумму вычетов относительно этих полюсов:

(4.42)

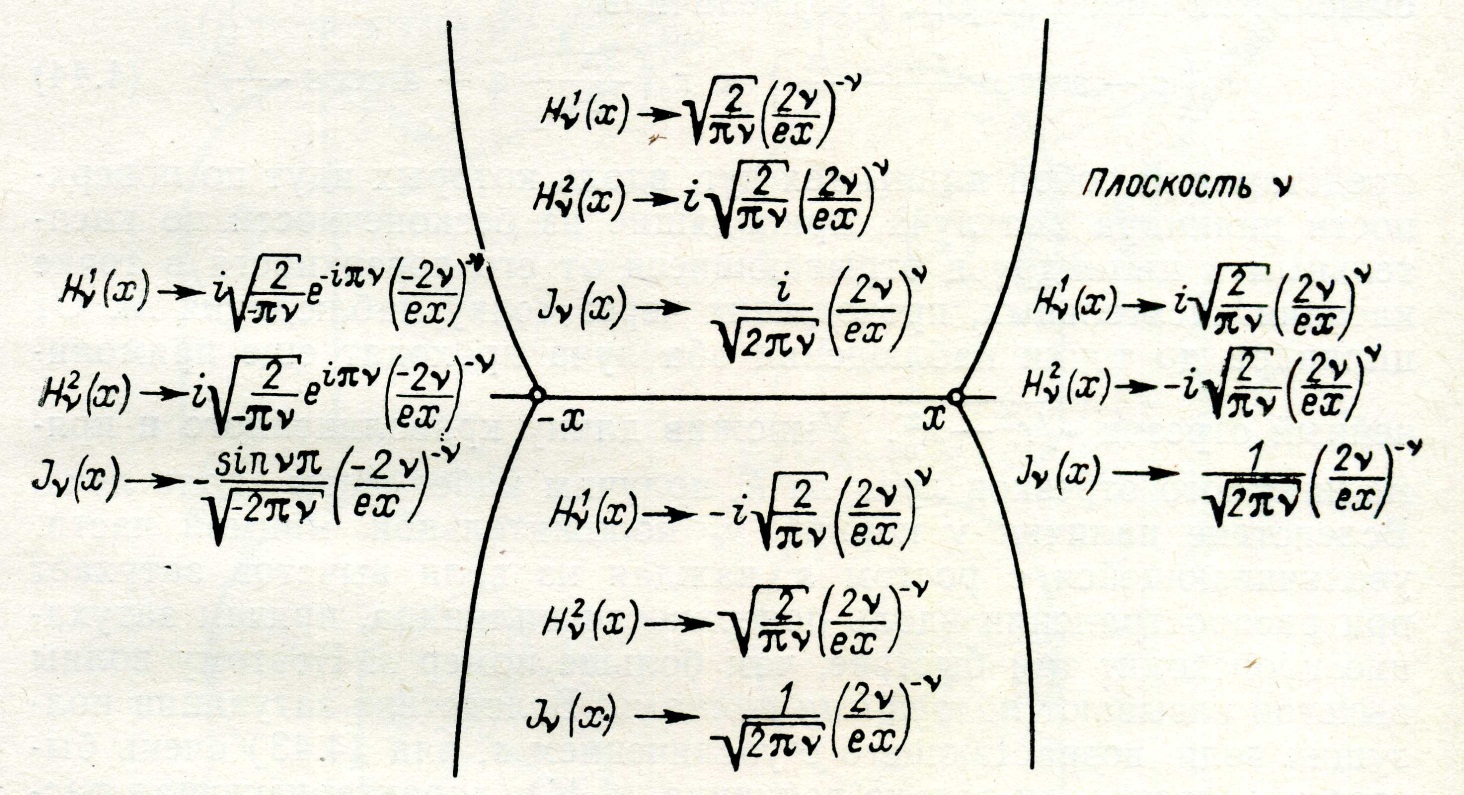
Рис. 4.14. Асимптотические выра­жения цилиндрических функций в бесконечности

на плоскости v

Эта формула выражает решение исследуемой задачи дифракции в виде суммы «волн вычетов», которые соответствуют, как будет показано ниже, затухающим собственным волнам. Преимущество ряда (4.42) состоит в том, что при kг_о 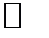1 он быстро сходится, по крайней мере в области тени.

Асимптотическое выражение p_Σ (r, φ), справедливое при больших значениях kr_o, имеет вид

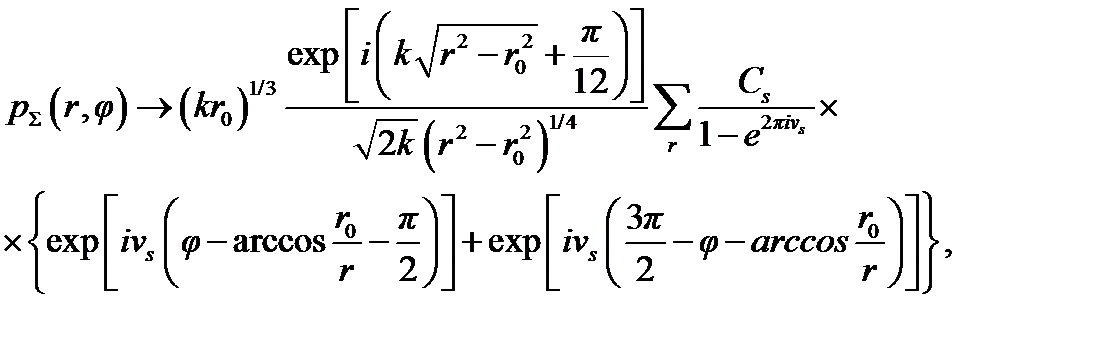(4.43)

где C_s — известные амплитуды ползущих волн.

Входящие в (4.43) величины имеют простой геометрический смысл. Как видно из рис. 4.15, величины

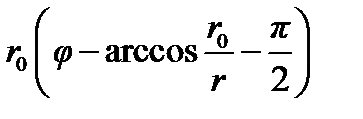и (4.44)

представляют собой длины тех дуг, вдоль которых идут по поверхности цилиндра два луча, приходящие из бесконечности по касательным к цилиндру и отрывающиеся от его поверхности в точке касания касательных, проходящих через точку наблюдения М. От цилиндра до точки наблюдения оба луча проходят ещё прямолинейный отрезок . Умножив длину криволинейного и прямолинейного отрезков луча на k, получим набег фазы вдоль луча, вследствие наличия у корней v_s положительной мнимой части, увеличивающейся с ростом s, каждая из волн вычетов затухает при распространении вдоль поверхности цилиндра, причём затухание происходит тем быстрее, чем больше номер s. Поэтому волны вычетов называют ползущими волнами. Вследствие затухания ползущих волн, возрастающего с увеличением s, ряд (4.43) очень быстро сходится, если только величина (4.44), характеризующая расстояние, пройденное волной вдоль поверхности цилиндра, положительна. Но это имеет место, как видно из рис. 4.15, лишь в том случае, когда точка наблюдения М находится в области геометрической тени за цилиндром.

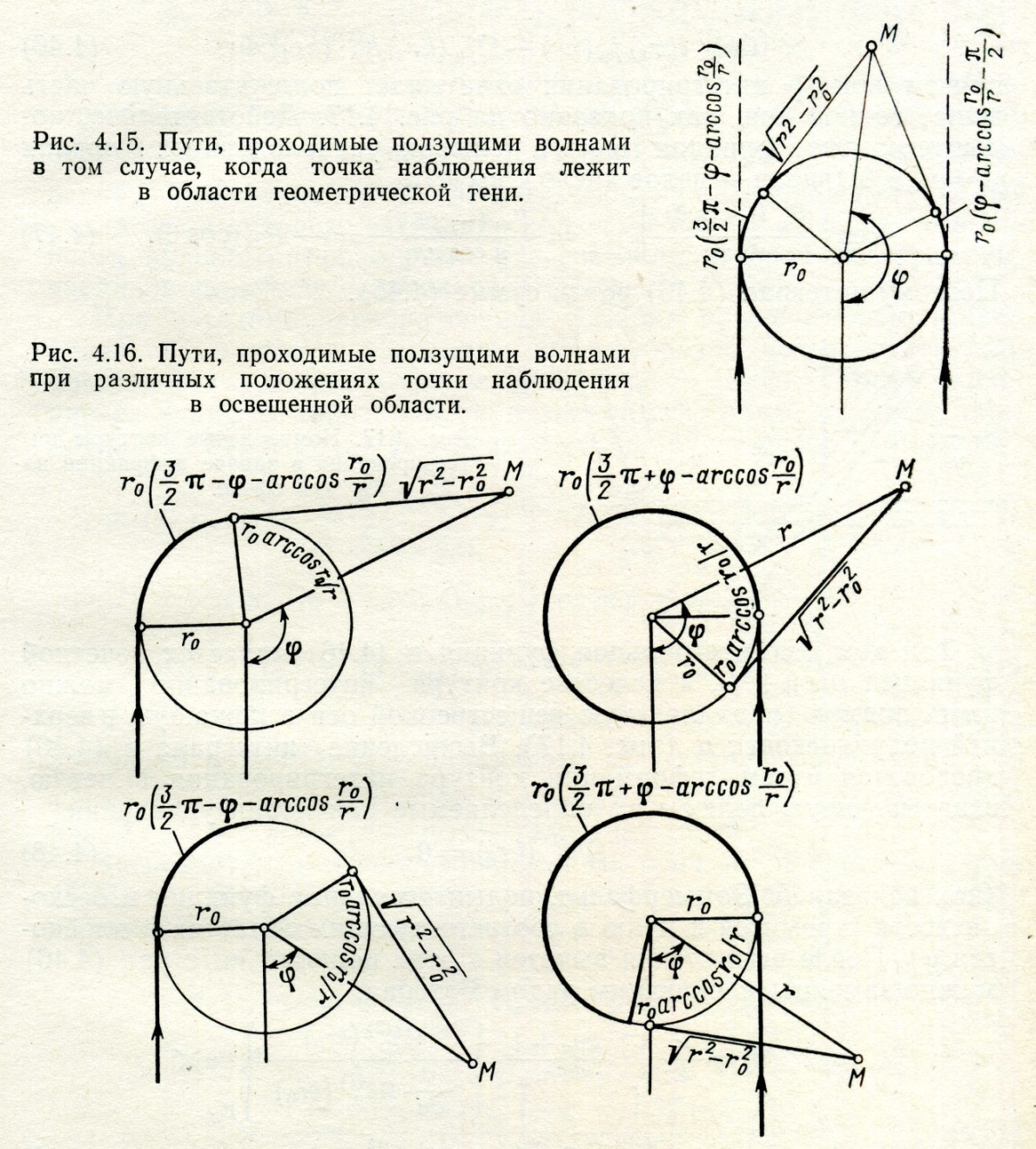
В случае, когда точка наблюдения находится в освещённой области, расстояния, пройденные волнами вдоль поверхности цилиндра, следует брать из рис. 4.16, на котором представлены четыре возможных случая расположения точки наблюдения относительно источника и рассеивателя.

Наличие в (4.43) знаменателя 1 — ехр 2πiv_s указывает на то, что кроме прямой ползущей волны имеются и такие волны, которые, прежде чем достичь точки наблюдения, несколько раз обходят вокруг цилиндра.

Применительно к идеально отражающей сфере преобразование Ватсона представляет, как и для цилиндра, сравнительно простой и наглядно интерпретируемый метод решения дифракционной задачи. Давление р_Σ в дифрагированной на идеальной сфере волне получается простым суммированием (4.17) и (4.23):

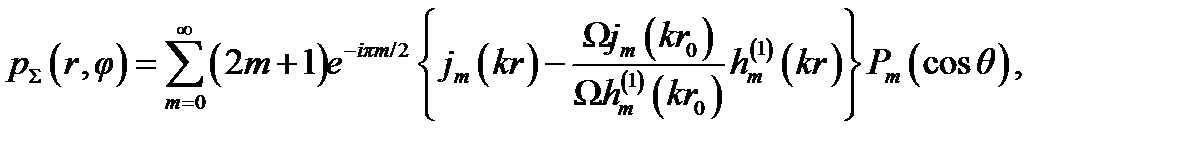(4.45)

Этот ряд можно представить как сумму вычетов интеграла:

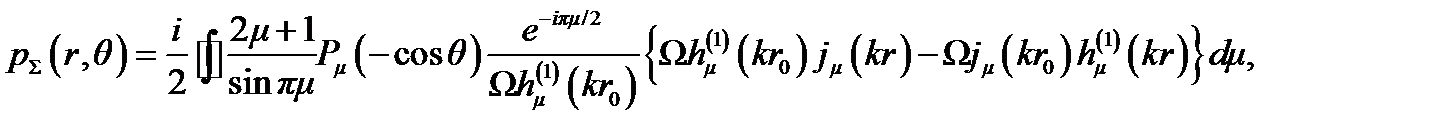(4.46)

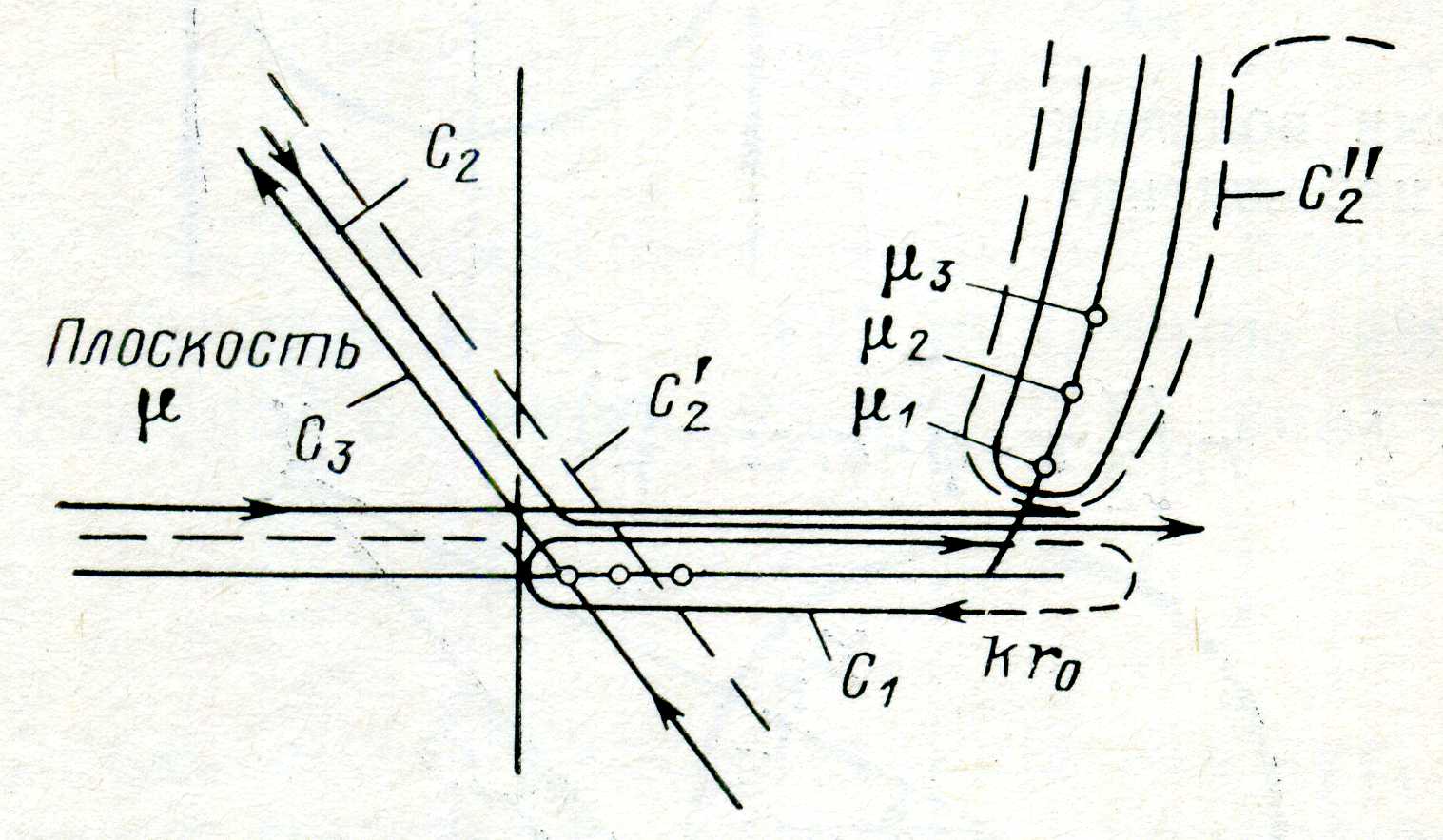
Рис. 4.17. Комплексные контуры ин­тегрирования в задаче дифракции на сфере.

причём контур интегрирования охватывает положительную часть вещественной оси, как показано на рис. 4.17. Действительно, подынтегральная функция имеет в полюсах, расположенных в точках μ = m 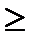0 (где т — целое число), вычеты

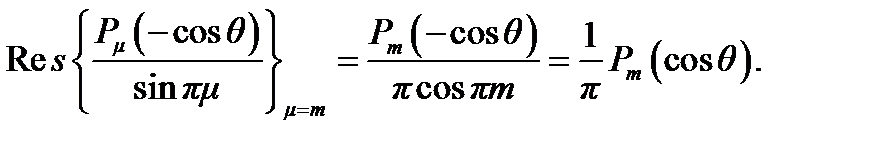(4.47)

Так как подынтегральная функция в (4.46) является нечётной функцией от μ +1/2, в качестве контура интегрирования можно взять прямую, параллельную вещественной оси и лежащую в верхней полуплоскости μ (рис. 4.17). Вычисление интеграла в (4.46) проводится путём деформации контура интегрирования в петлю, охватывающую полюсы μ_s, определяемые как корни уравнения

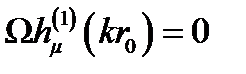(4.48)

(как показал А. Зоммерфельд, подынтегральная функция в бесконечности стремится к нулю в соответствующих областях в плоскости μ). После вычисления вычетов в этих полюсах интеграл (4.46) можно заменить следующим рядом Ватсона:

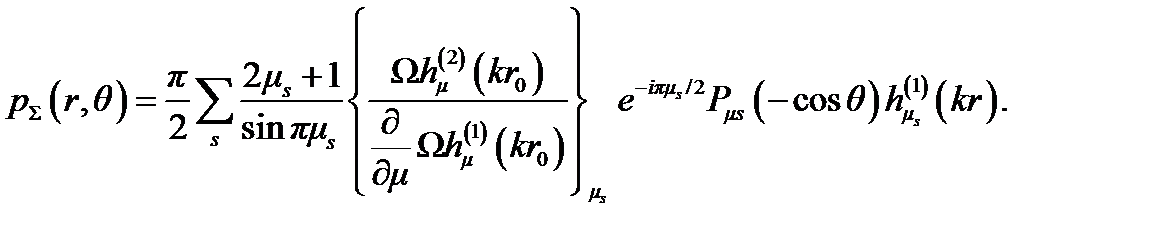(4.49)

Применительно к сфере весьма большого волнового размера В.А. Фок вычислил интеграл (4.46) несколько иным способом. Первоначальный контур С₁ он заменил двумя эквивалентными ему контурами (см. рис. 4.17):

1) ломаной линией С₂, проходящей несколько выше вещественной оси и ниже первого полюса μ₁ знаменателя (4.49);

2) прямой линией С_з, проходящей через начало координат и наклонённой под небольшим углом к мнимой оси.

Интеграл по контуру С₃ равен нулю ввиду чётности подынтегральной функции А_v, определяемой выражением

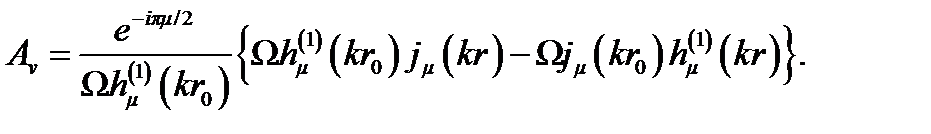
Интеграл по контуру C₂ был разбит на два слагаемых, одно из которых соответствовало ползущей волне(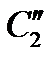), а второе — обратному отражению (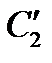) (см. рис. 4.17). Первый интеграл в точке наблюдения, совмещённой с источником, давал пренебрежимо малый вклад из-за сильного затухания ползущей волны, вызванного большими волновыми размерами рассеивателя. Второй интеграл вычислялся по методу стационарной фазы.

При изучении преобразования Ватсона применительно к идеально отражающим сфероидам целесообразно использовать сфероидальные функции в форме Мейкснера и Шефке. Тогда давление р_Σ в дифрагированной на идеальном сфероиде волне по ана­логии с (4.34) и (4.45) [и с учётом (4.30)] будет равно

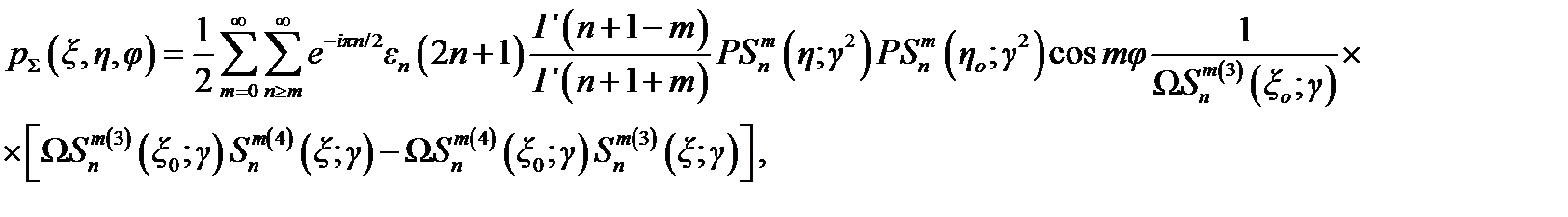
(4.50)

где 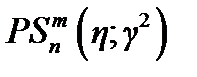— угловая сфероидальная функция первого рода;

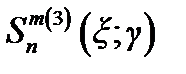и — радиальные сфероидальные функции 3-го и 4-го родов соответственно;

Y = 2πh_o/ λ — волновой размер сфероида;

Г (n + 1 — m) = (п — т)! — гамма-функция.

Воспользуемся преобразованием Ватсона и представим ряд (4.50) как бесконечную сумму контурных интегралов на комплекс­ной плоскости v одного из индексов:

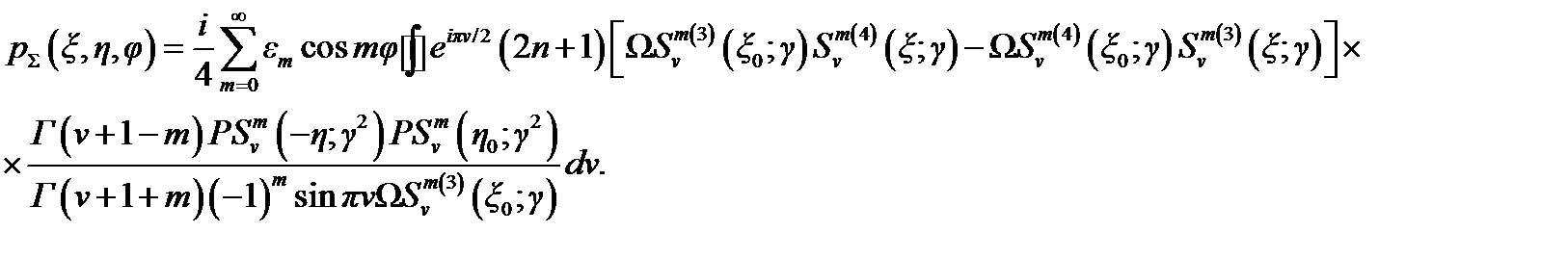
(4.51)

Всем контурам присвоим соответствующие им индексы т. Значе­ние каждого из интегралов ряда равно сумме вычетов подынте­гральной функции относительно простых полюсов, находящихся в точках v = n, где п — целое число. Как и в случае сферы, кон­туры интегрирования охватывают положительную часть вещест­венной оси комплексной плоскости v. Поэтому контур с индексом т= 0 практически ничем не отличается от контура С _t (см. рис. 4.17), проведённого для идеальной сферы. Этот контур(т = 0) изображён на рис. 4.18. Что касается остальных контуров т > 0), то в отношении них поступим следующим образом:

1)контуры с индексами т entier (γξ₀) будут охватывать все очки п 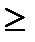0, где п — целое число, т. е. они ничем не будут отличаться от контура т = 0 (см. рис. 4.18);

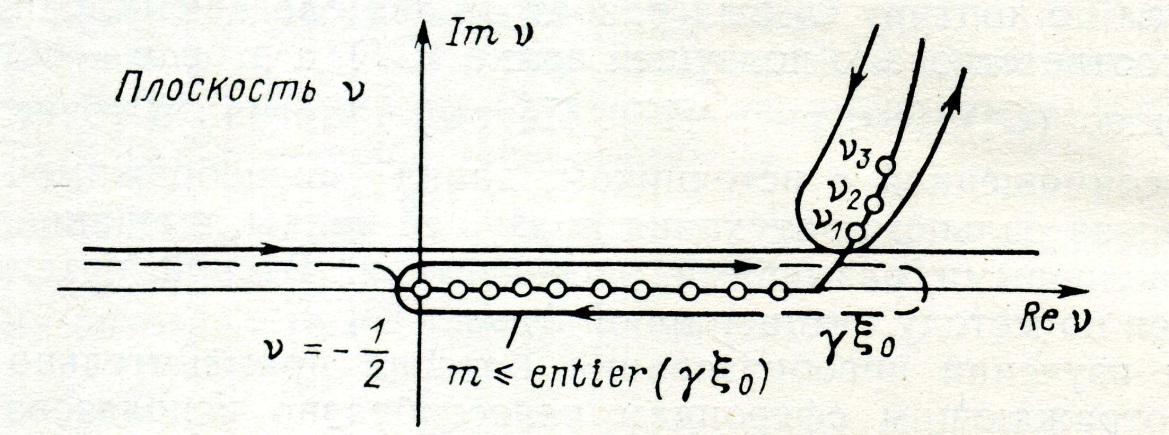
Рис. 4.18. Контур интегрирования m = 0 для идеального сфероида.

2) при т > entier (γξ₀) контуры будут включать лишь целочисленные п 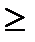т (рис. 4.19).

Искусственное вытягивание контуров интегрирования влево до точки v = —1/2 в первом случае (см. рис. 4.18) никак не скажется на значении интеграла, если вспомнить, что при n < т. Поэтому

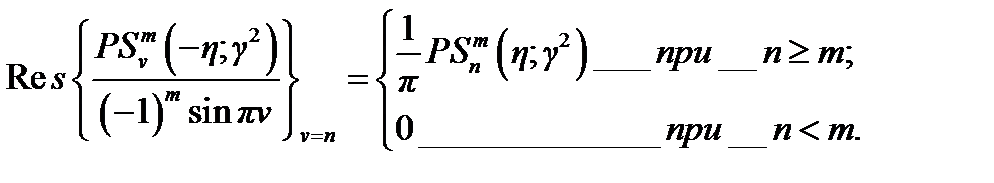
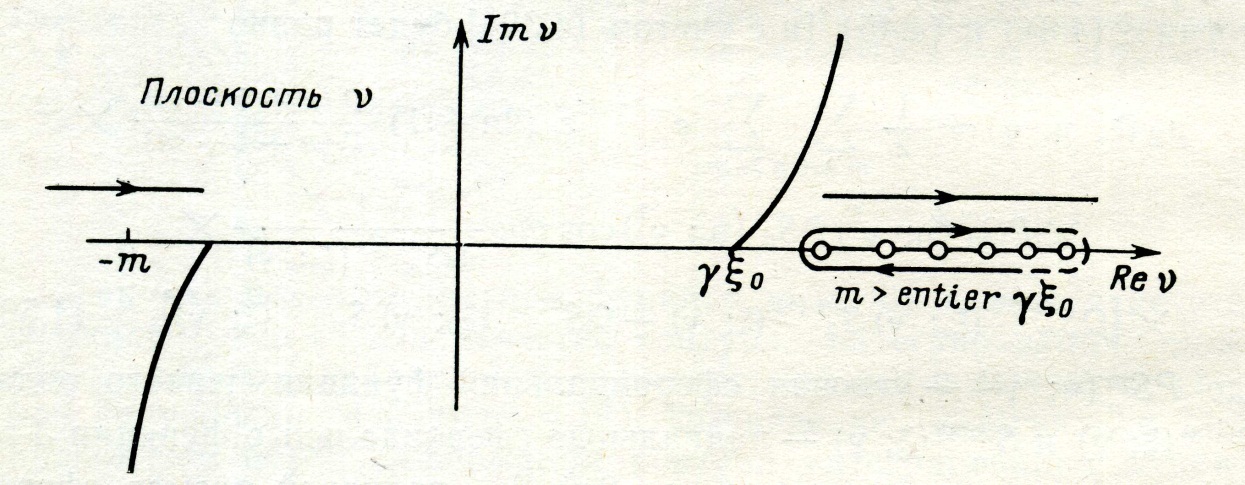
Рис. 4.19. Контур интегрирования т > entier (γξ₀) для идеального сфе­роида

Произведя замену независимой переменной v = t — 1/2, найдём, опираясь на свойства Г -функции и сфероидальных волновых функций, что подынтегральная функция является нечётной относительно t = v + 1/2. Нечётность подынтегральной функции по t позволяет видоизменить контуры интегрирования следующим образом:

1) контуры с индексами т entier (γξ₀) преобразуются в прямые, параллельные вещественной оси и лежащие в верхней полуплоскости v, затем они превращаются в полуокружности бесконечно большого радиуса и петли, охватывающие полюсы v_s (см. рис. 4.18), определяемые как корни уравнения

;

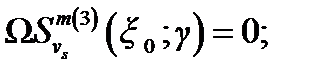2) контуры с индексами т > entier (γξ₀) преобразуются в две полупрямые, ограниченные точками v = m и v =—т (см. рис. 4.19).

Асимптотические формулы для радиальных сфероидальных функций 3-го и 4-го родов с одним комплексным (v) и одним ве­щественным (т) индексами при у 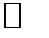1 имеют вид

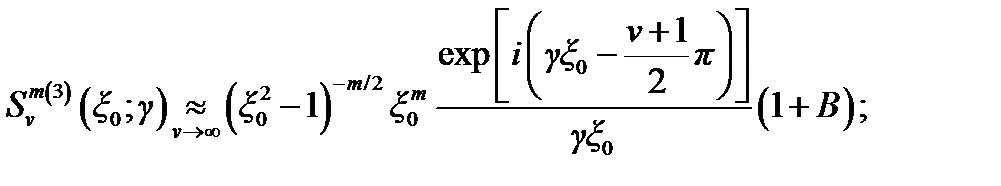
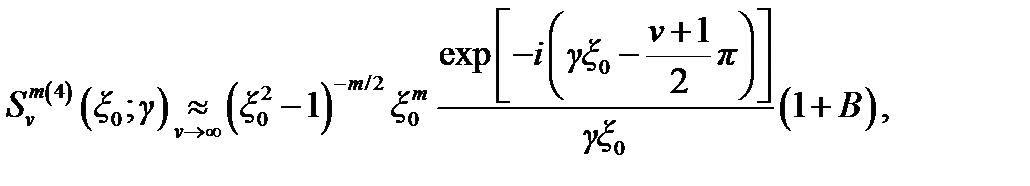
где В имеет порядок .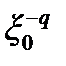

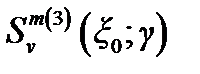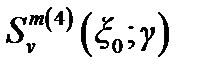Следовательно, функции и при 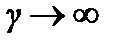можно представить в виде произведения:

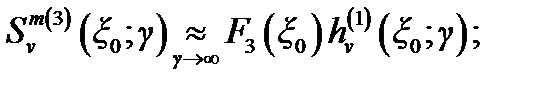
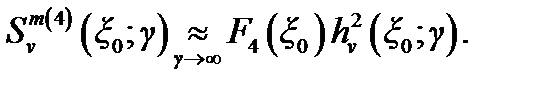
Поскольку функци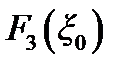и и 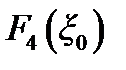не обращаются в ноль на ком­плексной плоскости v, то нули функции 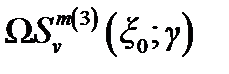совпадают асимптотически (γ 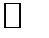1) c нулями функции , а следова­тельно, и с нулями цилиндрической функции 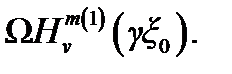Контурные интегралы первого типа [ т 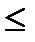entier (γξ₀)] можно заменить суммой вычетов в полюсах v_s и бесконечную сумму интегралов (4.51) представить в виде двух слагаемых:

 

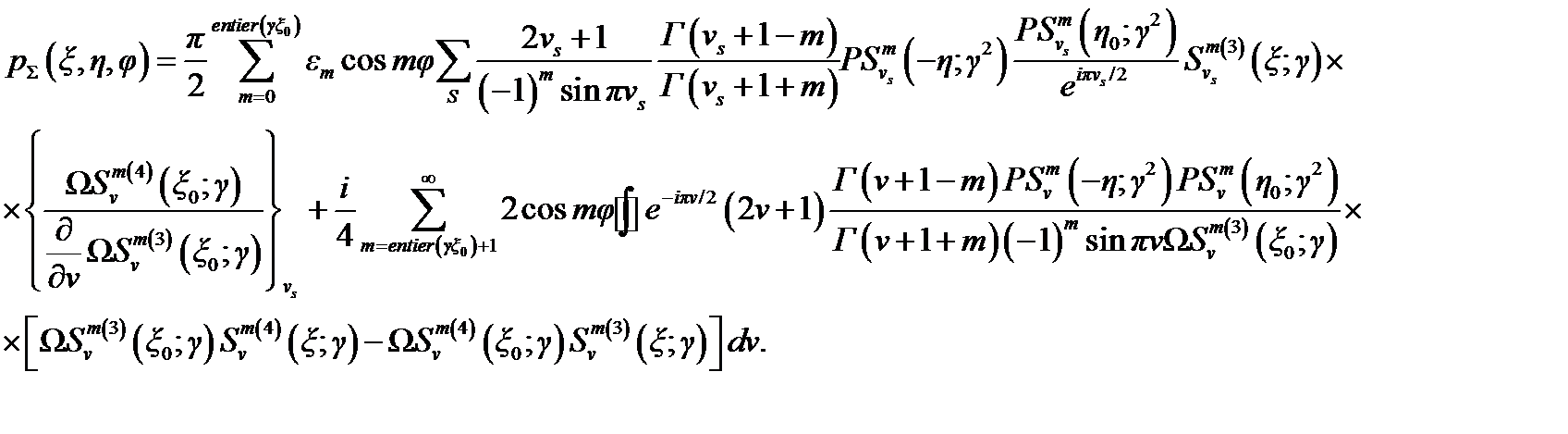
(4.53)

По аналогии со сферическими и цилиндрическими функциями Ханкеля радиальные сфероидальные функции 3-го рода изменяются по модулю медленно, пока | v |< γξ₀, а при | v |> γξ₀ быстро возрастают (при т = 0). При т > 0 рост радиальных функций начн­ётся с меньших значений | v |. Учитывая это, приходим к выводу, что второе слагаемое в (4.53) оказывается пренебрежимо малым по сравнению с первым; что же касается первого слагаемого, то в нём достаточно оставить члены с т 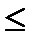entier 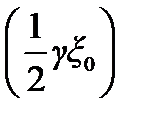. В результате соотношение (4.53) принимает вид

. (4.54)

Таким образом, преобразование Ватсона позволяет нам перейти от суммирования 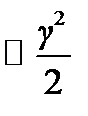у²/2 членов двойного ряда по незатухающим волнам к суммированию 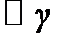членов ряда (4.54).

При решении осесимметричной задачи дифракции на идеальном сфероиде индекс т принимает только одно значение — 0 и в выражении (4.54) остаётся только ряд по волнам вычетов:

---

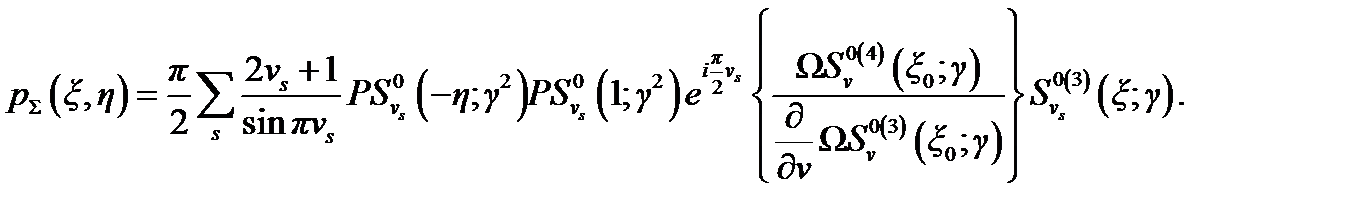
Дата добавления: 2016-01-03; просмотров: 33; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!