Тема 2. Числові характеристики дискретних випадкових величин та їх властивості
Закони розподілу ДВВ повністю характеризують випадкові величини і дозволяють розв'язувати усі пов'язані з ними задачі. Але в практичній діяльності не завжди вдається одержати закон розподілу, або закон надто складний для практичних розрахунків. Тому з'явилася потреба характеризувати ДВВ за допомогою числових характеристик, які характеризують особливості випадкових величин достатньо.
Найбільш часто використовують три числових характеристики: математичне сподівання, дисперсію та середнє квадратичне відхилення від математичного сподівання.
Ознайомимось із цими числовими характеристиками та :їх властивостями.
Математичне сподівання та його основні властивості.
Означення 1. Математичним сподіванням дискретної випадкової величини X називають число, яке дорівнює сумі добутків усіх можливих значень X на відповідні їм імовірності.
Математичне сподівання ДВВ X позначають М(Х) або т X , тобто
(1)
Якщо X приймає нескінчену кількість значень, то
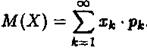
Математичне сподівання ДВВ X характеризує середнє значення випадкової величини X із врахуванням імовірностей його можливих значень. У практичній діяльності під математичним сподіванням розуміють центр розподілу випадкової величини.
Основні властивості математичного сподівання
Математичне сподівання постійної величини дорівнює самій постійній
|
|
|
M (С)=C
Постійний множник можна виносити за знак математичного сподівання
М(СХ)=СМ ( Х).
Властивості 1 і 2 випливають безпосередньо з Означення 1.
Математичне сподівання добутку декількох взаємно незалежних дискретних випадкових величин дорівнює добутку їх математичних сподівань, тобто
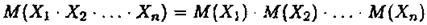
Доведення. Якщо дві величини X та У розподілені за законами
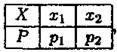
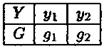
(для спрощення викладок взято лише по 2 можливих значення), тоді закон розподілу добутку X - Y буде
За формулою (1) одержимо математичне сподівання
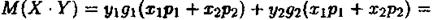
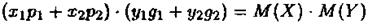
У випадку трьох випадкових величин маємо
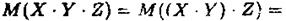
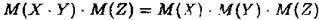
Методом математичної індукції тепер неважко завершити доведення.
Аналогічно, але дещо складніше, можна довести наступну властивість.
Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань, тобто
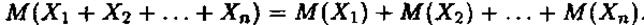
Приклад 2. Незалежні випадкові величини X та Y розподілені так
Знайти математичне сподівання випадкової величини XY .
Розв'язання. Спочатку знайдемо математичні сподівання кожної з цих величин. За формулою (1) маємо
М ( X )=5*0.6+2*0.1+4*0.3=4.4, M(Y )=8*0.8+10*0.2=8.4.
Випадкові величини X і Y незалежні, тому згідно властивості 3 математичного сподівання одержимо
Приклад 3.Знайти математичне сподівання суми числа очок, які можуть з'явитися при киданні двох гральних кубиків.
|
|
|
Розв'язання.Позначимо кількість очок, які можуть з'явитись на першому кубику X , а на другому -Y . Можливі значення цих величин 1,2,3,4,5,6 однакові, імовірність кожного з цих значень дорівнює 
. Тому
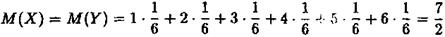
Згідно властивості 4 математичного сподівання, одержимо
М ( Х+ Y )=М(Х)+ M ( Y ) = 
Отже, математичне сподівання суми числа очок, що можуть з'явитись при киданні двох гральних кубиків, дорівнює 7.
Дисперсія та її властивості.
Математичне сподівання характеризує центр розподілу дискретної випадкової величини. Але цієї характеристики недостатньо, бо можливе значне відхилення можливих значень від центру розподілу. Для характеристики розсіювання можливих значень X відносно центру розподілу введемо нову числову характеристику.
Означення 2. Дисперсією дискретної випадкової величини X називають число, яке дорівнює математичному сподіванню квадрата відхилення ДВВ X від її математичного сподівання.
Дисперсію величини X позначають D ( X ) або D Х . Це означення математичновиглядає так
D ( X ) = M (( X -М(Х))2). (2)
Основні властивості D ( X ).
1) Дисперсія будь-якої ДВВ X невід'ємна
|
|
|
D ( X ) >0
Дійсно, ( X -М(Х))2 невід'ємна, тому згідно означення математичного сподівання та властивостей імовірностей рk, k =1,2,...,п, D ( X ) також невід'ємна.
2) Дисперсія постійної величини С дорівнює нулеві
D ( C )= 0.
Дійсно, якщо X=С, то М(С)=С, тому С-М(С)=0.
3) Постійний множник С можна виносити за знак дисперсії, при цьому постійний множник треба піднести у квадрат
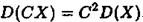(3)
Дійсно, СХ-М(СХ)=С ( Х-М(Х)), тому
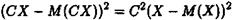
Постійний множник С2 можна виносити за знак математичного сподівання, тому з формули (2) випливає потрібна рівність (3).
4) Дисперсія ДВВ X дорівнює різниці між математичним сподіванням квадрата випадкової величини X та квадрата її математичного сподівання
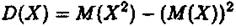(4)
Дійсно, 
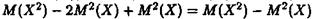
Зауваження 4. Формула (2) визначає дисперсію випадкової величини X , а за формулою (4) її доцільно знаходити.
5) Дисперсія алгебраїчної суми ДВВ X та У дорівнює сумі їх дисперсій
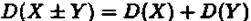
Доведення. Спочатку доведемо цю властивість для X + Y . Згідно з формулою (4) маємо
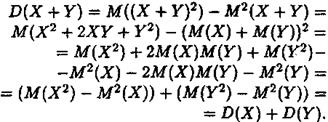
Тепер розглянемо дисперсію різниці X та Y
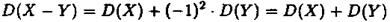
Зауваження 5. П'ята властивість дисперсії має місце для алгебраїчної суми не лише двох, але й скінченого числа дискретних випадкових величин.
|
|
|
Приклад 4. Знайти дисперсію випадкової величини X , що задана законом
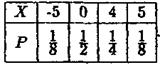
Розв'язання. Будемо шукати D ( X ) з використанням формули (4). Математичним сподіванням X згідно з формулою (1) буде
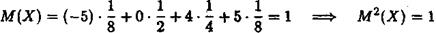
Щоб знайти математичне сподівання X 2 , тобто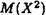 
, запишемо закон розподілу X 2 у вигляді таблиці
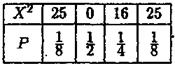
Відмітимо, що усі значення X 2 отримані шляхом піднесення до квадрату відповідних значень X . Елементи другого рядка - імовірності цих значень - не змінюються.
За формулою (1) знаходимо
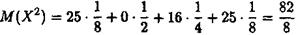
Згідно з формулою (4) тепер одержуємо
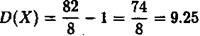
Дата добавления: 2023-01-08; просмотров: 30; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!