Примеры решения основного уравнения диффузии.

Лекция 7

Диффузия в металлах и ее основные законы

Как уже указывалось, колебаниями атомов около положений равновесия не исчерпывается многообразие форм теплового движения в твердом теле: атомы могут уходить из положений равновесия и блуждать по кристаллической решетке. Такое перемещение атомов обусловливает возможность процессов диффузии в твердом теле.

Практически диффузию в твердом теле используют уже много столетий. Поверхностная цементация стали, т. е. насыщение поверхностного слоя стального изделия углеродом, — наиболее яркий пример использования диффузии в технике. Процессы диффузии, протекающие при обычных операциях термической обработки стали (отпуске закаленной стали, отжиге и т. д.), менее очевидны.

Несмотря на многовековое использование подвижности атомов твердого тела, о факте этой подвижности до 80-х годов прошлого столетия высказывались лишь отдельные догадки. Фарадей, изучавший в 1820 г. спекание металлических порошков, получил твердые растворы, возникшие в твердой фазе без ее плавления, т. е. путем диффузии. Но это обстоятельство он оставил без внимания и никаких предположений о возможности диффузии в твердом теле не высказал. П. П. Аносов уже в 1837 г. опубликовал сообщение о газовой цементации стали. Этот процесс, как известно, целиком основан на явлениях диффузии. Основоположник научного металловедения, Д. К. Чернов, первым в 1868 г. обсуждая возможные причины сваривания двух раскаленных кусков металла, осуществляемого без их расплавления, определенно заявил о существовании диффузии в твердом теле.

Первое систематическое исследование явлений диффузии в твердом теле было проведено в конце прошлого столетия; при этом впервые удалось количественно определить константы диффузии. Было подчеркнуто, что в металле способны диффундировать лишь те элементы, которые в нем растворяются.

При рассмотрении миграции атомов в кристаллической решетке чистого металла и твердого раствора необходимо различать следующие явления:

а) миграцию атомов в чистом металле, обусловливающую процесс, называемый «самодиффузией»;

б) миграцию атомов растворенного элемента, приводящую к так называемой «гетеродиффузии», и

в) миграцию атомов растворителя, приводящую к самодиффузии в твердом растворе. Конечно, второе и третье явления тесно переплетаются между собой.

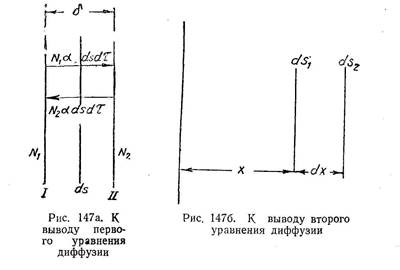
Рассмотрим основные законы гетеродиффузии, которые справедливы и для самодиффузии. Не входя пока в обсуждение вопроса о механизме процесса диффузии в твердом теле, примем лишь, что вероятность перехода атома из какого-либо положения равновесия в соседнее при заданной температуре для заданного вещества, являющегося твердым раствором компонента В в компоненте А, есть величина при заданной концентрации твердого раствора постоянная. Обозначим вероятность такого перехода за промежуток времени, равный 1 сек., через a Рассмотрим обмен атомами компонента В между двумя соседними параллельными между собой атомными плоскостями (рис. 147 а).

Пусть на квадратном сантиметре плоскости / находится N_l атомов компонента В, а на плоскости // — N ₂ . Как и при хорошо известном упрощенном выводе основного уравнения кинетической теории газов, будем считать, что атомы могут с равной вероятностью перемещаться вдоль трех взаимно перпендикулярных прямых, одна из которых совпадает с нормалью к плоскостям I и II¹. Тогда за d t сек. с площадки в ds см² cплоскости I уйдет на плоскость II 1/6 a N ₁ dsd t атомов компонента B .

В обратном, направлении за тот же промежуток времени перейдет 1/6 a N ₂ dsd tатомов. Если через N₀ обозначить число. Авагадро, то выраженная в грамм-атомах масса dM компонента В, протекшая за d t сек. от плоскости / к плоскости // сквозь площадку ds , параллельную этим плоскостям и лежащую между ними, выразится так:

(201)

Помножим и разделим правую часть уравнения (201) на межплоскостное расстояние d;

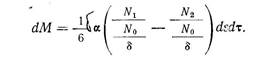
Так как объемы атомных слоев, содержащих N₁ и N₂ атомов, равны d см³ (площадь основания 1 см², высота d см), то дроби, стоящие в скобках, выражают, очевидно, значения грамм-атомной концентрации компонентов В в атомных слоях / и // с₁и с₂:

Знак минус поставлен здесь ввиду того, что величина Dс выражает изменение концентрации при переходе от плоскости / к плоскости //, т. е. разность с₂- с₁, а не величину с₁— с₂, стоящую в скобках.

Вновь помножим и разделим правую часть уравнения (201) на d и примем во внимание, что вследствие малости межплоскостного расстояния в кристаллической решетке можно положить Dс/d = dc / dx , где х—координатная ось, совпадающая с нормалью к плоскостям / и //:

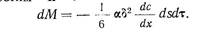(202)

Обозначив произведение 1/6a d² через D (коэффициент диффузии) , получим окончательно:

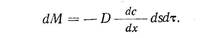(203)

Выражение (203) является одним из уравнений переноса, к числу которых относятся также уравнения теплопроводности, внутреннего трения в газах и т. д. Оно применимо к диффузии в любой среде — твердой, жидкой и газообразной, и было получено впервые путем анализа опытных данных.

Как видно из уравнения (203), коэффициент диффузии равен выраженной в молях массе вещества, диффундирующей за 1 сек. сквозь площадку в 1 см² при градиенте концентрации dc / dx , равном молю на сантиметр. Он выражается в квадратных сантиметрах в секунду. Так как значения коэффициента диффузии, выраженные в абсолютной системе единицы, крайне малы, часто относят его не к секунде, а к суткам (см²/сутки).

Для практических расчетов закон диффузии в форме (203) не применим. Для перехода к более удобной форме рассмотрим плоский слой толщиной dx , сквозь который в направлении оси х происходит диффузия компонента В (рис. 1476). Вывод сделаем для общего случая, предполагая, что коэффициент диффузии может зависеть от концентрации диффундирующего элемента и, следовательно, может измениться по глубине диффузионного слоя.

Пусть координаты равных и параллельных площадок ds₁ и ds₂, ограничивающих этот слой, равны х и х + dx . Тогда сквозь площадку ds , за d t сек. внутрь объема ds • dx продиффундирует масса растворенного элемента dM ₁ , равная, в соответствии с уравнением (203):

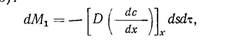
а через площадку ds ₂ уйдет из объема:

Так как концентрация с убывает с увеличением х, то в объеме dsdx за время d t масса компонента В увеличится на величину dM (через площадку ds ₁ войдет больше компонента В, чем уйдет через площадку ds ₂ ):

Изменение концентрации компонента В в объеме ds • dx , равное dM / ds • dx , определится отсюда так

• a dc / dx — скорость изменения концентрации, очевидно:

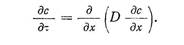(204)

Уравнение (204) называется вторым законом диффузии. Оно также аналогично одному из основных уравнений теплопередачи.

В простейшем частном случае, когда коэффициент диффузии не зависит от концентрации диффундирующего элемента, уравнение (204) примет вид:

(204а)¹

(¹Вывод сделан в предположении, что концентрация растворенного элемента меняется лишь вдоль направления х («линейная диффузия). Можно показать, что в общем случае, когда концентрация меняется вдоль всех трех координатных осей уравнение (204а) будет иметь такой вид:

Дифференциальное уравнение, выражающее второй закон диффузии, может быть при определенных условиях проинтегрировано; в результате интегрирования может быть найдена зависимость

c = f(x,t).

Теория интегрирования уравнений, подобных второму уравнению диффузии, разработана детально.

Перемещение атомов в процессе диффузии подчиняется тем же законам, что и броуновское движение частиц, взвешенных в жидкости. В теории броуновского движения доказывается, что среднее квадратичное смешение частицы, описывающей сложный зигзагообразный путь под действием неуравновешенных ударов молекул среды, пропорционально квадратному корню из длительности движения.

Покажем для линейной модели диффузионного процесса (т. е. для перемещения атомов вдоль прямой линии), что действительно среднее квадратичное смещение атома из

исходного положения пропорционально квадратному корню из времени.

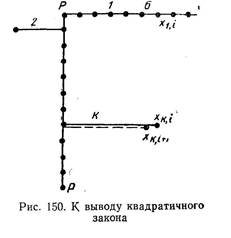
Пусть атомы растворенного компонента В в начальный момент времени находятся на плоскости РР (рис. 150) и далее через равные промежутки времени t₀ перескакивают в направлении, перпендикулярном этой плоскости, на расстояния, равные d, с равной вероятностью как вправо, так и влево.

Рассмотрим размещение атомов после i-того и (i + l)-ro скачков. Обозначим расстояния атомов от исходной плоскости РР после i-того скачка через х_1._i , х₂,_i . . . х _k _, _i . Очевидно, после следующего скачка расстояния изменятся так:

Знаки + и — указывают, что возможны скачки как вправо ( + ), так и влево (—). Очевидно,

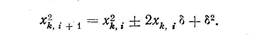
Найдем среднее значение квадрата смещения атома после (i + 1)-го скачка. Если п-—общее число атомов, то:

(209)

поскольку d x_k_,_I = 0 [числа отрицательных и положительных членов суммы равны между собой, так как скачки вправо и влево при переходе от i-того к (i +1) -му положению равновероятны]. Если принять во внимание, что после первого скачка

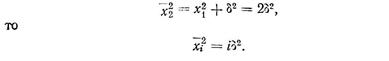
Если обозначить время, в течение которого протекал процесс, через t , то очевидно, i = t /t_o , так что

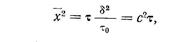
где константа с² = d²/t₀. Уравнение (210) справедливо, конечно, и для перемещения атомов при самодиффузии.

Такой же результат может быть получен и для трехмерного движения атома в кристалле, т. e. для реальной модели диффузионного процесса (величину х² нужно будет только в этом случае заменить на s², где s — смещение атома в произвольном направлении).

Сопоставляя выводы уравнений (203) и (210), следует отметить, что для рассмотренного при выводе уравнения (210) случая одномерного перемещения частиц коэффициент диффузии D должен быть равен не 1/6a d², а 1/2a d².

Если принять во внимание, что вероятность ухода частицы из положения равновесия a и среднее значение промежутка времени между двумя скачками частицы t₀ связаны соотношением

то уравнение (210), часто называемое параболическим законом, можно переписать так:

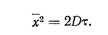
Для трехмерного перемещения частиц при диффузии, когда D = 1/6a d² очевидно следует, написать

(211)

. (211а)

Наконец, коэффициент диффузии определится из уравнения (211) так:

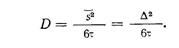
(212)

Таким образом, среднеквадратичное значение смещений атомов при диффузии (и самодиффузии) пропорционально квадратному корню из длительности процесса диффузии и коэффициент диффузии (или самодиффузии) равен среднему значению квадрата смещения атомов, поделенному на удвоенную длительность процесса диффузии.

Учитывая (212), можно так переписать уравнение, характеризующее распределение диффундирующего элемента в диффузионном слое при независимости коэффициента диффузии от концентраций:

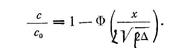
(213)

Следовательно, отношение концентрации с диффундирующего элемента на глубине х от поверхности насыщаемого тела к концентрации с₀ этого элемента на поверхности является функцией отношения глубины х к среднеквадратичному смещению атомов в процессе диффузии или, при постоянстве коэффициента диффузии, функцией отношения

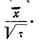
Естественно считать, что значения перескоков атомов того же порядка, что и межатомные расстояния в решетке, т. е. порядка 1Å. Зная коэффициент диффузии, можно определить частоту перескоков. Для углерода в a-железе при 900°С D~10^-⁶ см²/с. Если d~10^-⁸ см, то i/t_o составит 10¹⁰ 1/с, т. е. каждый атом углерода меняет свое положение примерно 10'° раз в 1 с.

Аналогичный расчет для самодиффузии в металлах с г. ц. к. и гекс. п. у. решетками для температуры, близкой к точке плавления, показывает, что каждый атом в этих условиях меняет место 10⁸ раз в 1 с. Если эта цифра кажется очень большой, то следует вспомнить, что частота колебаний (дебаевская частота) таких атомов составляет 10¹²—10¹³ с-¹. Таким образом, атом меняет положение только один раз на 10⁴—10⁵ колебаний. Даже вблизи точки плавления большую часть времени атом колеблется около равновесного положения.

Примеры решения основного уравнения диффузии.

Предположим, что начальное распределение концентрации в теле задано в виде

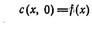
(5.4)

и коэффициент диффузии не зависит от концентрации. Решение уравнения (5.2) в общем случае для неограниченного тела получают в виде

с(х, t )= T ( t ) X ( x ), (5.5)

где функция T ( t ) зависит только от времени, а Х(х) — только от координаты (для простоты ограничиваемся одномерной диффузией).

Общее решение уравнения диффузии практически используется редко, так как имеется мало практических задач, в которых требуется рассчитать изменение со временем распределения концентрации в телах достаточно больших размеров. Однако оно используется для получения частных решений.

Решение для диффузии из бесконечно тонкого слоя. В этом случае распределение концентрации имеет вид

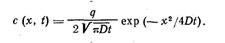
(5.6)

Здесь q — количество вещества (в тех же единицах, что и концентрация), приходящееся на 1 см² слоя.

Функция ехр ( — x ² /4 Dt ) четная, поэтому распределение концентрации, создаваемое бесконечно тонким слоем в обоих полупространствах, симметрично относительно начала координат или середины слоя. Со временем начальное распределение постепенно расплывается, оставаясь симметричным относительно x = 0. Величина максимума кривой распределения в точке х=0 С_макс = q /2 (p Dt)^0,5уменьшается обратно пропорционально корню квадратному из времени (рис. 5.1, а).

Решение для диффузии из слоя конечной толщины. Распределение концентрации при толщине слоя 2h имеет вид

с ( х , t) = c_o/2 [erf (h + x)/2 VDt + erf (h — x)/2 VDt] , (5.7)

где erf — функция ошибок (error function) Гаусса:

Из графика функции c ( x , t ) (см. рис. 5.1,6) видно, что при t — ¥ концентрация всюду обращается в нуль (erf 0=0), так как конечное количество вещества q = —2 c ₀ h распределяется по бесконечной области.

Решение для диффузии из полубесконечного пространства. Начальное распределение концентрации задано так, что при всех х<_0 с(х, 0)=С_о, а при всех х>0 с(х, 0) =0. Для этого случая решение имеет вид

(5.8)

Следует отметить, что для всех t >0 концентрация в плоскости раздела (x = 0) постоянна и равна с_о.2 (см. рис. 5.1.в).

Некоторые общие закономерности. Выше отмечено, что значение максимума на кривой распределения концентрации при диффузии из бесконечно тонкого слоя уменьшается обратно пропорционально корню квадратному из времени. При диффузии из слоя конечной толщины наблюдается тот же эффект, но он становится заметным через значительно большее время. Теперь определим, по какому закону изменяется расстояние до плоскости, в которой концентрация' в е раз меньше, чем в плоскости x = 0. При x = 0 с(0, t )= q /2 VDt ехр(О). В плоскости, где концентрация в е раз меньше, с(х, t )= c(0, t)/ e . Приравнивая концентрации в обеих рассматриваемых плоскостях, получаем

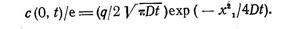
Решая это уравнение относительно х₁, получаем

(5.9)

т. е. расстояние между этими плоскостями изменяется пропорционально корню квадратному из времени.

При решении уравнения диффузии предполагалось, что материал в направлении диффузионного потока имеет бесконечную протяженность.

Произведем оценку размера тела, который может считаться бесконечно большим. Для этого зададимся количеством продиффундировавшего вещества, которым можно пренебречь начиная с какого-то размера тела х₁. Если общее количество вещества, продиффундировавшего за время t, равно

-¥

Количество же вещества, которым условились пренебречь,

. (5.10)

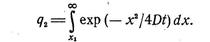
Искомую величину x₁, можно найти из заданного отношения q₂/q₁,-Если q ₂/q_l = 10^-², т. е. составляет 0,1%. то x₁ = 4VDt. Другими словами, при протяженности тела большей 4 VDt условие бесконечности выполняется. Следует иметь в виду, что х₁зависит от D и от времени. Поэтому для разного времени требуемая протяженность материала разная.

Здесь рассмотрены лишь некоторые решения уравнения диффузии, наиболее часто встречающиеся и на практике.

(5.12)

Диффузия в поле напряжений.

Рассмотренные решения уравнения диффузии справедливы лишь в случае, когда перемещение диффундирующего вещества определяется исключительно градиентом концентрации. В общем случае поток вещества будет представлять собой сумму потоков, возникающих под действием градиента концентрации и добавочного силового поля. Частным случаем такого поля является поле неоднородных напряжений (деформаций).

Причины возникновения поля напряжений в твердом теле следующие: его неоднородная деформация, фазовые превращения, неравномерный нагрев и т. д. Микроскопические деформации могут быть вызваны внедренными атомами или вакансиями. Поле напряжений, возникающее вокруг внедренного атома в твердом растворе, способствует притяжению атома к дислокации. В результате может оказаться, что суммарный диффузионный поток будет направлен в сторону не меньшей, а большей концентрации. Это так называемый случай восходящей диффузии.

Второе уравнение диффузии с учетом влияния поля напряжений имеет вид

(5.16)

где e— упругая деформация. Коэффициент диффузии D " характеризует поток, связанный только с влиянием градиента напряжений (деформаций). По вычислениям С. Т. Конобеевского величина D " пропорциональна относительной разнице атомных радиусов компонентов сплава (r_B—r_A )/ r_A Атомы с большим радиусом при наличии деформации стремятся переместиться в растянутые слои сплава, а атомы с меньшим радиусом — в сжатые. Если первоначально компоненты сплава были распределены в кристаллической решетке сплава статистически равномерно, так как градиент концентрации был равен нулю, то при наличии неоднородного напряженного состояния за счет второго члена уравнения в твердом растворе будет протекать диффузия, приводящая не к выравниванию концентраций, а к разделению компонентов. Создающаяся в результате восходящей диффузии химическая неоднородность, характеризуемая в каждом участке градиентом концентрации, приводит к возникновению встречного диффузионного потока, обусловливаемого первым членом правой части уравнения (5.16) и стремящегося восстановить первоначальное равномерное распределение компонентов в кристаллической решетке твердого раствора. Равновесное распределение компонентов при неизменной деформации решетки наступит при равенстве обоих потоков, т. е. при условии

(5 17)

Сэффектом восходящей диффузии С. Т. Конобеевский связывает упрочнение деформированных твердых растворов при нагреве.

Переменная концентрация твердого раствора всегда связана с неоднородно напряженным состоянием, причем градиент концентрационных напряжений определяется упругими константами твердого раствора, зависимостью периода решетки твердого раствора от концентрации последнего и, наконец, градиентом концентрации.

При электронографическом исследовании структуры тонких слоев цинка, последовательно нанесенных конденсацией на полированную поверхность медной пластинки, обнаружено, что первые слои цинка при комнатной температуре целиком растворились в меди (интерференционные линии цинкового слоя исчезли через 10 с после конденсации). Полированная поверхность приобрела характерный оттенок латуни. Такая интенсивная диффузия при комнатной температуре обусловлена чрезвычайно большими искажениями кристаллической решетки, вызванными полировкой.

Очевидно, искаженность кристаллической решетки увеличивает коэффициент диффузии. Но не следует представлять этот эффект объемным, равномерно охватывающим всю массу деформированного металла. Это видно из анализа приведенных в литературе экспериментальных данных об энергии остаточных упругих напряжений после деформирования металла (т. е. об энергии искажений кристаллической решетки) . Оказалось, что ее запас не превышает 100 — 200 кал/(г-атом), составляя лишь ничтожную долю теплоты диффузии, измеряемой несколькими десятками тысяч калорий. Рентгенографические исследования показали, что энергия эта распределена по объему деформированного металла очень неравномерно: около 90% остаточной энергии деформирования сосредоточено в тончайших слоях у плоскостей сдвига, охватывающих 2—3% общего числа атомов. Здесь искаженность кристаллической решетки значительна. В этих слоях энергия деформации достигает 10 ккал/(г-атом). Очевидно, вдоль плоскостей сдвига и происходит в основном диффузия в пластически деформированном металле.

Необходимо отметить, что диффузия в реальных технологических процессах происходит при температурах, достаточных для возврата и даже рекристаллизации деформированных металлов, снижающих или устраняющих совсем искаженность кристаллической решетки.

Кроме поля напряжений (деформаций) на диффузионную подвижность атомов в твердых телах могут существенно влиять и другие поля, вчастности электрические.

При изучении диффузии Сu в Ge обнаружено, что при температуре выше 800°С наложение электрического поля приводит к смещению концентрационной кривой в сторону отрицательного электрода. При температуре ниже 800°С такого смещения не наблюдали. Обнаруженная закономерность позволяет считать, что при высокой температуре Сu присутствует в Ge в виде положительных ионов.

Дата добавления: 2022-12-03; просмотров: 43; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!