Интегрирование некоторых тригонометрических выражений
Интегрирование простейших дробей
Дробь первого типа:
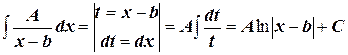
Дробь второго типа:
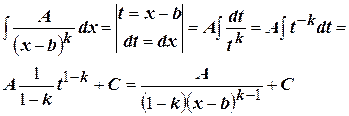
При условии, что 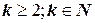 .
.
Дробь третьего типа:
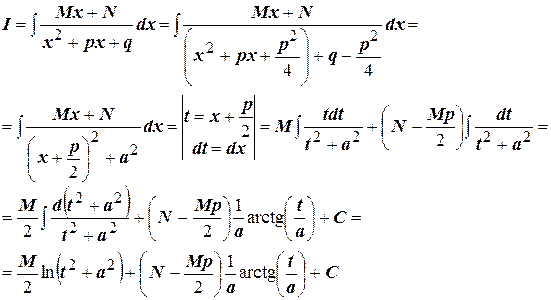
Окончательно,
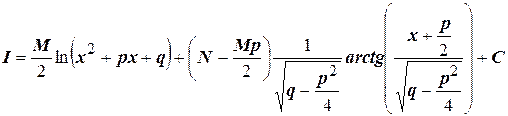
При условии, что 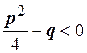 ,
, 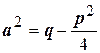 .
.
Дробь четвёртого типа: 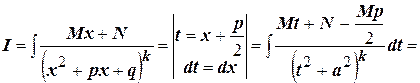
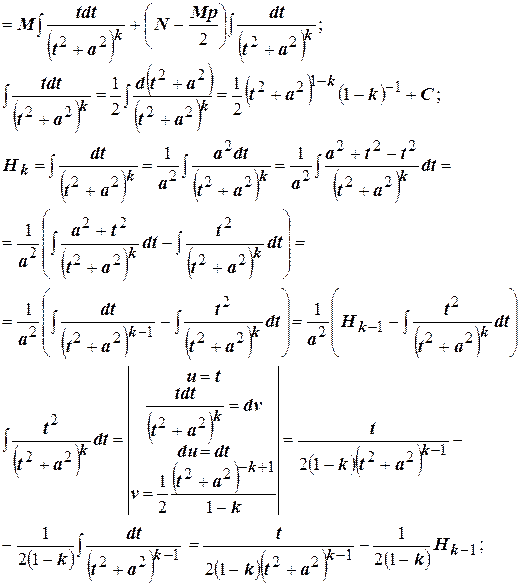
Таким образом, получили рекуррентную формулу для интеграла:
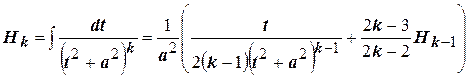 , (4.12)
, (4.12)
где 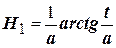
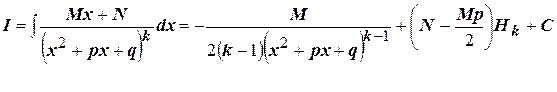
Соотношения выполняются при условии, что 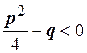 ,
, 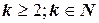 .
.
4.9. Интегрирование рациональных дробей
методом разложения на простейшие
Рациональной дробью называется отношение вида 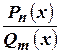 , где
, где 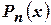 и
и 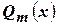 - многочлены с действительными коэффициентами соответственно степени
- многочлены с действительными коэффициентами соответственно степени 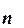 и
и 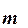 . Если
. Если 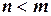 дробь называется правильной, а если
дробь называется правильной, а если 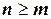 , то - неправильной. Если дробь неправильная, то справедливо соотношение
, то - неправильной. Если дробь неправильная, то справедливо соотношение 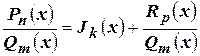 , где
, где 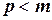 , а
, а 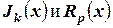 - многочлены степени
- многочлены степени 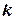 и
и 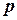 .
.
Интеграл от многочленов берется с использованием таблицы и свойств интегралов. Следовательно, для того чтобы интегрировать рациональные дроби, нужно уметь интегрировать правильные рациональные дроби.
Лемма первая: Пусть отношение 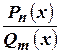 - правильная рациональная дробь и пусть
- правильная рациональная дробь и пусть 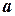 - действительный корень кратности
- действительный корень кратности 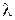 знаменателя
знаменателя 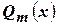 . Тогда справедливо разложение:
. Тогда справедливо разложение: 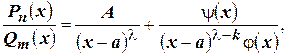 где
где 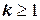 - некоторое целое число, а
- некоторое целое число, а 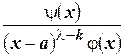 - правильная дробь.
- правильная дробь.
Доказательство:
Так как 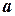 - действительный корень кратности
- действительный корень кратности 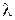 знаменателя
знаменателя 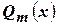 , то
, то 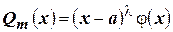 , причем
, причем 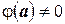 .
.
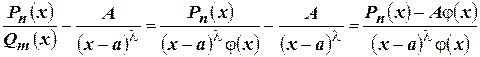 .
.
Определим 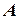 так, чтобы число
так, чтобы число 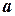 являлось корнем некоторой кратности
являлось корнем некоторой кратности 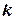 многочлена
многочлена 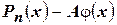 . В этом случае
. В этом случае
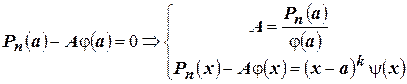 .
.
Подставив это в дробь, получаем
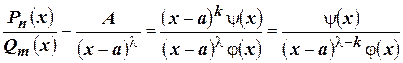 .
.
И, соответственно,
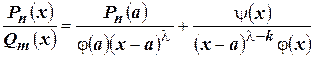 .☻
.☻
Лемма вторая: Пусть 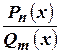 - правильная рациональная дробь и пусть число
- правильная рациональная дробь и пусть число 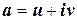 - комплексный корень кратности
- комплексный корень кратности 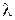 знаменателя
знаменателя 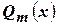 , то есть
, то есть 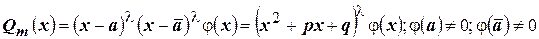 . Тогда
. Тогда 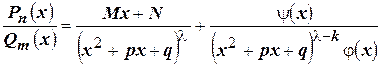 ,
, 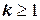 - некоторое целое число такое, что
- некоторое целое число такое, что 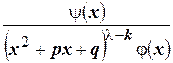 - правильная дробь.
- правильная дробь.
Доказательство:
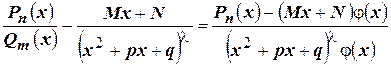 . Определим
. Определим 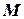 и
и 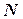 таким образом, чтобы число
таким образом, чтобы число 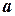 являлось корнем некоторой кратности
являлось корнем некоторой кратности 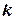 многочлена
многочлена 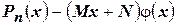 , т.е.
, т.е.
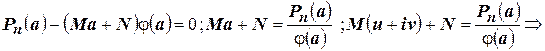
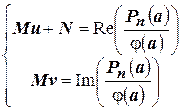
Эта система всегда имеет решение. Таким образом, 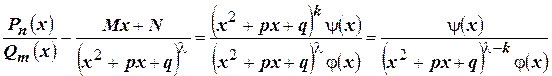 .☻
.☻
Из этих двух лемм следует, что если
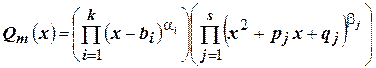 , (4.13)
, (4.13)
причём ни один из квадратных трёхчленов 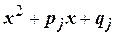 не имеет действительных корней, то правильная дробь
не имеет действительных корней, то правильная дробь 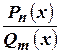 может быть представлена в виде суммы простейших дробей
может быть представлена в виде суммы простейших дробей
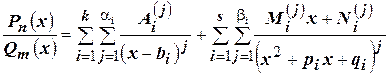 . (4.14)
. (4.14)
В разложении (4.14) 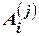 ,
, 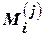 и
и 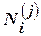 - некоторые действительные числа. Их можно определить следующим образом: дроби, стоящие в правой части (4.14), привести к общему знаменателю, после этого приравнять коэффициенты при одинаковых степенях
- некоторые действительные числа. Их можно определить следующим образом: дроби, стоящие в правой части (4.14), привести к общему знаменателю, после этого приравнять коэффициенты при одинаковых степенях 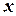 в числителях левой и правой частей и решить получившуюся систему уравнений.
в числителях левой и правой частей и решить получившуюся систему уравнений.
Еще один способ определения этих чисел состоит в следующем. После приведения к общему знаменателю дробей, стоящих в правой части (4.14), приравнять числители левой и правой частей. Система уравнений для определения чисел 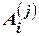 ,
, 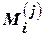 и
и 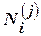 получается, если в это равенство подставить столько различных значений переменной
получается, если в это равенство подставить столько различных значений переменной 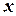 , сколько неизвестно коэффициентов
, сколько неизвестно коэффициентов 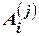 ,
, 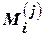 и
и 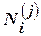 . Второй способ очень удобен, если все корни уравнения
. Второй способ очень удобен, если все корни уравнения 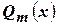 имеют кратность, равную единице. Тогда подставляют в получившееся уравнение вместо
имеют кратность, равную единице. Тогда подставляют в получившееся уравнение вместо 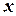 по очереди корни многочлена
по очереди корни многочлена 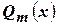 .
.
Пример:
Разложить на простейшие дробь 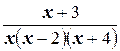 .
.
Согласно (4.14)
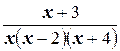
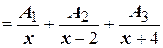
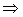
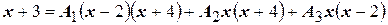
Полагая 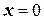 , получим
, получим 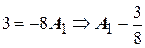 . Аналогично, если взять
. Аналогично, если взять 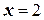 , находим
, находим 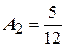 , а если
, а если 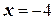 , то
, то 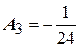 . Таким образом,
. Таким образом,
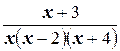
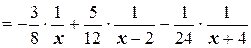
Интегрирование некоторых тригонометрических выражений
1) Интегрирование 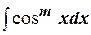 и
и 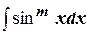 .
.
Рассмотрим два случая: 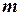 - нечетное число (
- нечетное число ( 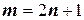 ) и
) и 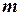 - четное (
- четное ( 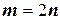 ).
).
Пусть 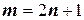 , тогда:
, тогда:
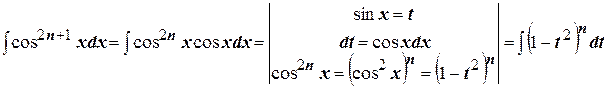
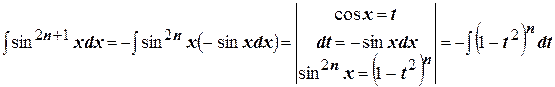
Далее используя бином Ньютона, берём интегралы от алгебраических многочленов.
Пусть теперь 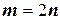 . Воспользуемся формулами «понижения».
. Воспользуемся формулами «понижения».
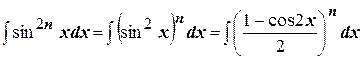
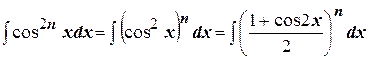 .
.
Далее опять используем бином Ньютона, а интегралы вида 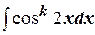 берем только что описанным методом.
берем только что описанным методом.
2) Интегрирование 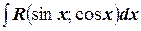 , где выражение
, где выражение 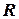 рационально зависит от
рационально зависит от 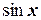 и
и 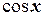 .
.
Воспользуемся универсальной тригонометрической подстановкой:
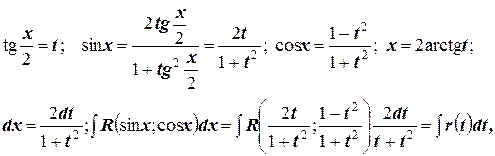
Выражение  является рациональной дробью и соответствующим образом интегрируется.
является рациональной дробью и соответствующим образом интегрируется.
Замечания:
1. Если выражение 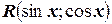 нечетно относительно
нечетно относительно 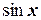 , то есть
, то есть 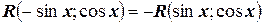 , то более удобной является подстановка
, то более удобной является подстановка 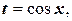 т.к. в этом случае
т.к. в этом случае
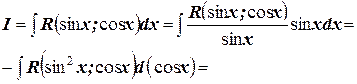
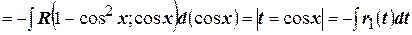 .
.
2. Если выражение 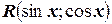 нечетно относительно
нечетно относительно 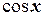 , то есть
, то есть 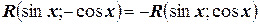 , то используется подстановка
, то используется подстановка 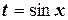 .
.
3. Если 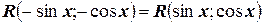 , то наиболее удобной является подстановка
, то наиболее удобной является подстановка 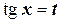 .
.
3) Интегрирование 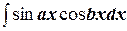 ,
,  и
и 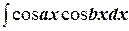 осуществляется с помощью формул
осуществляется с помощью формул
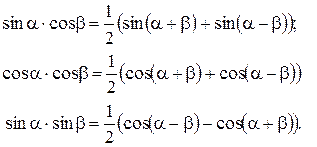
Дата добавления: 2022-12-03; просмотров: 36; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
