Вопрос 3. Следствия из аксиом стереометрии

Аксиомы стереометрии

План лекции

Вопрос 1. Предмет стереометрии

Вопрос 2. Аксиомы стереометрии

Вопрос 1. Предмет стереометрии

Основными фигурами стереометрии являются точка, прямая, плоскость. Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д.

Из курса планиметрии известно, что плоскость — это множество точек, в котором выполняется система аксиом планиметрии, описывающая свойства точек и прямых.

Аналогично, пространство — это множество точек, в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей.

Специфика всей стереометрии заключается в том, что пространственные фигуры мы будем изображать на плоскости.

Вопрос 2. Аксиомы стереометрии

Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное положение теории.

Система аксиом стереометрии даёт описание свойств пространства и основных его элементов. Понятия «точка», «прямая», «плоскость», «расстояние» принимаются без определений: их описание и свойства содержатся в аксиомах. Аксиомы играют для них роль «неявных определений». С другой стороны, понятия «точка», «прямая», «плоскость» имеют наглядный смысл, отражённый на рисунках.

Изучение пространства приводит к необходимости расширения системы аксиом планиметрии. Система аксиом стереометрии, таким образом, состоит из всех аксиом планиметрии и новой группы аксиом, в которых выражены свойства взаимного расположения точек, прямых и плоскостей в пространстве.

Аксиома R₁. В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.

Эта аксиома даёт право рассматривать в любой плоскости пространства отрезки, прямые, треугольники, многоугольники, окружности и другие плоские фигуры со всеми их свойствами, которые изучались в планиметрии. Например, если прямая a и не принадлежащая ей точка M лежат в некоторой плоскости α, то в этой плоскости можно провести через точку M прямую, параллельную прямой a, и притом только одну.

Аксиома R₂ (аксиома плоскости). Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.

На рисунке: плоскость α проходит через точки A, B, C — концы трёх стержней, не принадлежащие одной прямой, а плоскость β проходит через другие концы M, K и P этих стержней, также не принадлежащие одной прямой.

Три точки, принадлежащие одной прямой, называются коллинеарными, а три точки, не принадлежащие одной прямой, — неколлинеарными. Так, три вершины треугольника неколлинеарны, а середины оснований трапеции и точка пересечения её диагоналей коллинеарны. Вообще, все точки одной прямой коллинеарны.

Плоскость, которая проходит через три точки A, B и C, не принадлежащие одной прямой (C ∉ AB), обозначают символически (ABC); если этой плоскостью является плоскость α, то пишут α = (ABC) или (ABC) = α. (В таком случае также говорят, что три неколлинеарные точки в пространстве определяют плоскость.)

Через любые две точки A и B в пространстве можно провести плоскость α. По аксиоме R₁ в этой плоскости выполняются все аксиомы планиметрии. Согласно одной из этих аксиом через точки A и B можно провести единственную прямую.

Аксиома R₃. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

Данной аксиомой утверждается, что для любой плоскости в пространстве можно выбрать любое количество точек в этой плоскости, равно как и сколько угодно точек вне её. В случае, если точка A лежит в (принадлежит) плоскости α, то записывают: A ∈ α и говорят, что плоскость α проходит через точку A. Если точка A не принадлежит плоскости α, то записывают: A ∉ α и говорят, что плоскость α не проходит через точку A. На рисунке

плоскость α проходит через точку A, но не проходит через точку B.

Аксиома R₄ (аксиома прямой и плоскости). Если прямая проходит через две точки плоскости, то она лежит в этой плоскости.

Итак, из аксиомы R₄ следует: (M ∈ α, N ∈ α, MN = a) ⇒ a ⊂ α (рис. 16). При этом также говорят, что плоскость α проходит через прямую a (через прямую MN).

В пространстве прямая может не лежать в данной плоскости, но иметь с этой плоскостью ровно одну общую точку. В этом случае говорят, что прямая и плоскость пересекаются.

Определение. Прямая и плоскость, имеющие ровно одну общую точку, называются пересекающимися.

Если прямая a пересекает плоскость α в точке B то символически записывают: α ∩ a = B или B = a ∩ α.

Существуют ли в пространстве прямые, пересекающие данную плоскость? С одной стороны, ответ очевиден — конечно, существуют; однако посмотрим, каким образом аксиомы позволяют обосновать существование таких прямых.

Прямую, пересекающую данную плоскость α, можно получить следующим образом. На основании аксиомы R₃ выберем произвольную точку A вне плоскости α и произвольную точку B в плоскости α.

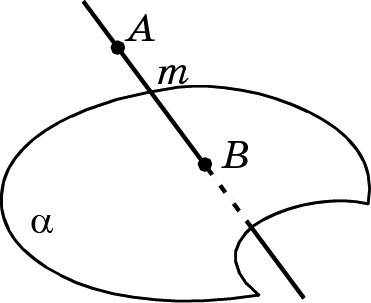
Тогда прямая m = AB является искомой: она имеет общую точку B с плоскостью α и не лежит в этой плоскости, так как точка A выбрана вне плоскости α. Значит, прямая AB имеет с плоскостью α единственную общую точку — точку B, а поэтому пересекает плоскость α в точке B. Таким образом, прямые, пересекающие данную плоскость, в пространстве существуют.

Аксиома R₅ (аксиома пересечения плоскостей). Если две плоскости имеют общую точку, то пересечение этих плоскостей есть их общая прямая.

Аксиома R₅ утверждает, что если две плоскости α и β имеют общую точку M, то они имеют некоторую общую прямую a, которая проходит через точку M (рис. 19). Кроме того, из этой аксиомы следует, что у плоскостей α и β нет общих точек вне их общей прямой a. В таком случае говорят, что плоскости α и β пересекаются по прямой a и записывают: α ∩ β = a или a = α ∩ β.

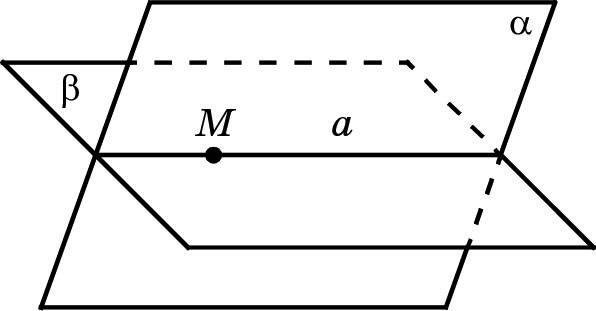
Если мы возьмём две фигуры Ф₁ и Ф₂, имеющие общие точки и лежащие соответственно в двух различных пересекающихся плоскостях, то все эти общие точки лежат на одной прямой и представляют собой либо отрезок, либо луч, либо отдельные точки, либо всю прямую, либо объединение нескольких отрезков, лучей или точек фигур. Вот почему, например, плоскость, пересекающая грань куба, имеет с этой гранью либо общую точку, либо общий отрезок.

Определение. Две плоскости, имеющие общую точку (следовательно, общую прямую), называются пересекающимися плоскостями.

Аксиома R₆ (аксиома разбиения пространства плоскостью). Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что: а) любые две точки, принадлежащие разным множествам, разделены плоскостью α; б) любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.

Проиллюстрируем смысл этой аксиомы.

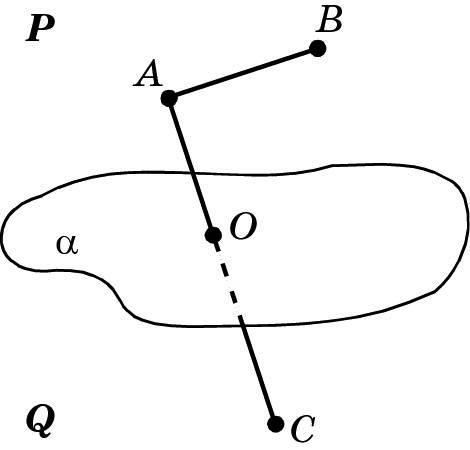
На рисунке изображена плоскость α. Она разбивает множество всех не принадлежащих ей точек пространства на два непустых множества P и Q, которые не имеют общих точек. Это разбиение обладает следующим свойством: если две точки, например A и B, принадлежат одному и тому же множеству P, то отрезок AB не пересекает плоскость α. Это означает, что точки A и B не разделены плоскостью α. Если же точки, например A и C, принадлежат разным множествам (A ∈ P, C ∈ Q), то отрезок AC пересекает плоскость α. Это означает, что точки A и C разделены плоскостью α.

Всё пространство (в нашем случае) является объединением точечных множеств P, Q и плоскости α. Объединение P ∪ α множества P и плоскости α называется полупространством, ограниченным плоскостью α. Плоскость α, ограничивающая это полупространство, называется его границей. Аналогично, объединение Q ∪ α является также полупространством с границей α.

Таким образом, пространство является объединением двух полупространств, границей каждого из которых является плоскость α. Изменение положения плоскости α влечёт за собой разбиение пространства в объединение новых полупространств.

Аксиома R₇ (аксиома расстояния). Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, проходящей через эти точки.

Смысл этой аксиомы состоит в следующем. По аксиоме R₁ в каждой плоскости выполняются аксиомы планиметрии. Следовательно, на каждой плоскости любым двум точкам A и B ставится в соответствие положительное число — расстояние между ними на этой плоскости. Хотя через точки A и B проходят одновременно различные плоскости (смотри рисунок выше), аксиома R₇ утверждает, что расстояние между точками A и B будет одно и то же на каждой из этих плоскостей.

Расстояние между точками A и B можно обозначить либо AB, либо ρ(A; B), либо | AB | в зависимости от контекста, если речь идёт о длине отрезка AB.

При выбранной единице измерения расстояние между любыми двумя точками выражается положительным числом, которое показывает, сколько единиц измерения длин и частей этой единицы измерения содержится в данном расстоянии. Так как число, выражающее расстояние между точками, зависит от выбранной единицы измерения, то единица измерения длин (см, дм, м и т. д.) пишется после этого числа. Например, если единица измерения длин — см, а численное значение расстояния между точками A и B равно 9, то пишут AB = 9 см. Если же единичный отрезок не имеет названия, то пишут AB = 9, имея в виду AB = 9 ед.

Вопрос 3. Следствия из аксиом стереометрии

Простейшие следствия из аксиом будут играть в дальнейшем важную роль. Они почти очевидны, но доказываются.

Следствие 1. Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

Доказательство. Пусть даны прямая a и не принадлежащая ей точка A.

Выберем на прямой a любые точки B и C.

Через точки B и C проходит только одна прямая — прямая a. Так как точка A по условию теоремы не принадлежит прямой a, то точки A, B и C не принадлежат одной прямой.

По аксиоме R₂ через точки A, B и C проходит только одна плоскость — плоскость ABC, которую обозначим α. Прямая a имеет с ней две общие точки — точки B и C, следовательно, по аксиоме R₄ эта прямая лежит в плоскости α. Таким образом, плоскость α проходит через прямую a и точку A и является искомой.

Докажем, что другой плоскости, проходящей через прямую a и точку A ∉ a, не существует.

Предположим, что есть другая плоскость — α₁, проходящая через точку A и прямую a. Тогда плоскости α и α₁ проходят через точки A, B и C, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость α единственная. Теорема доказана.

Две прямые в пространстве называются пересекающимися, если они имеют ровно одну общую точку.

Следствие 2. Через любые две пересекающиеся прямые можно провести плоскость, и притом только одну.

Доказательство. Пусть данные прямые a и b пересекаются в точке C.

Выберем на прямых a и b любые точки A и B, отличные от C: A ∈ a, B ∈ b. Тогда три точки A, B и C не принадлежат одной прямой (почему?), и по аксиоме R₂ через них можно провести только одну плоскость. Обозначим её α.

Точки A и C прямой a принадлежат плоскости α, значит, плоскость α проходит через прямую a (аксиома R₄). Плоскость α проходит и через прямую b, так как точки B и C этой прямой принадлежат плоскости α.

Таким образом, плоскость α проходит через прямые a и b, следовательно, является искомой.

Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые a и b, плоскость β.

Так как плоскость β проходит через прямую a и не принадлежащую ей точку B, то по теореме 1 она совпадает с плоскостью α. Единственность плоскости α доказана. ▼

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Если прямые a и b параллельны, то пишут a ‖ b.

Следствие 3. Через две параллельные прямые можно провести единственную плоскость.

Доказательство. Пусть a и b — данные параллельные прямые. Из определения параллельных прямых следует, что через прямые a и b можно провести плоскость. Обозначим её α и убедимся, что она единственна.

Допустим противное. Пусть существует другая плоскость, отличная от α, которая содержит каждую из прямых a и b. Обозначим эту плоскость β.

Выберем на прямой a точки B и C, на прямой b — точку A. В силу параллельности прямых a и b точки A, B и C не принадлежат одной прямой.

Каждая из плоскостей α и β содержит обе прямые a и b, значит, каждая из них проходит через точки A, B и C. Но по аксиоме R₂ через эти точки можно провести лишь одну плоскость. Следовательно, плоскости α и β совпадают. Теорема доказана. ▼

Из аксиомы R₂ и теорем 1, 2 и 3 следует, что плоскость в пространстве можно задать:

Ÿ тремя точками, не принадлежащими одной прямой;

Ÿ прямой и не принадлежащей ей точкой;

Ÿ двумя пересекающимися прямыми;

Ÿ двумя параллельными прямыми.

В дальнейшем вы узнаете, что задать плоскость в пространстве можно и другими определяющими её элементами.

Применяя аксиомы стереометрии и первые следствия из них, вы сможете решать стереометрические задачи, т. е. задачи, в которых исследуются некоторые свойства геометрических фигур, расположенных в пространстве. К стереометрическим относятся, например, задачи на построение сечений многогранников плоскостями.

Сечением многогранника плоскостью является многоугольник, представляющий собой множество всех точек пространства, принадлежащих одновременно данным многограннику и плоскости, плоскость при этом называется секущей плоскостью.

Как уже говорилось при обсуждении аксиомы R₅, плоскость не может пересечь грань многогранника по ломаной, а имеет с ней либо общий отрезок, либо общую точку (вершину многогранника), либо не имеет с ней общих точек. Число сторон многоугольника-сечения не может превышать числа граней многогранника. Причём если пересечением плоскости и многогранника является точка (вершина многогранника) или отрезок (ребро многогранника), то эту плоскость не будем называть секущей.

Дата добавления: 2022-12-03; просмотров: 35; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!