Определение: Под иррациональным неравенством понимается неравенство, в котором неизвестные величины (или некоторые функции величин) находятся под знаком радикала.
Лекция.
Иррациональные уравнения и неравенства.
Определение. Иррациональным называется уравнение, в котором неизвестное (переменная) содержится под знаком корня или под знаком операции возведения в рациональную (дробную) степень.
Для решения иррациональных уравнений обычно используются следующие приемы:
1)возведение в соответствующую степень обе части уравнения;
2) введение новой переменной;
3) сведение к системе уравнений;
4) применение свойств функций, входящих в уравнение.
При решении иррациональных уравнений необходима проверка всех найденных корней путем их подстановки в исходное уравнение или нахождение ОДЗ и следующий анализ корней (при решении методом приведения к равносильной смешанной системе уравнений и неравенств необходимость в этом отпадает).
Простейшим иррациональным уравнением является уравнение вида:
 ,
,
при решении которого важную роль играет четность или нечетность n.
Если n - нечетное, то данное уравнение равносильно уравнению
 .
.
Если n - четное, то, так как корень считается арифметическим, необходимо учитывать ОДЗ (область допустимых значений):  . Уравнение
. Уравнение  в этом случае равносильно системе:
в этом случае равносильно системе:
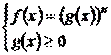 .
.
Пример 1.
Решить уравнение  .
.
Решение. Так как n =2 - четное, то обе части уравнения возводим во 2ю степень: 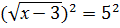



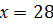
Ответ: 28
Пример 2.
Решить уравнение  .
.
Решение. Так как в данном примере n =3 - нечетное, то после возведения обеих частей уравнения в третью степень получим равносильное данному уравнение:  .
.
|
|
|
Ответ:  .
.
Пример 3.
Решить уравнение  .
.
Решение. Так как n =2 - четное, то исходное уравнение равносильно системе:

Ответ:  .
.
Уравнения вида 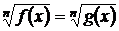 , решаются следующим образом:
, решаются следующим образом:
n – нечетное 

n - четное  или
или 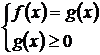 .
.
Пример 4.
Решить уравнение: 
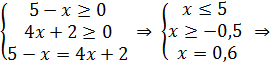
Ответ: 0,6
Пример 5.
Решить уравнение: 
Решение. Запишем данное уравнение в виде:  Возводя обе части в квадрат и учитывая, что
Возводя обе части в квадрат и учитывая, что 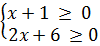 получим уравнение 2х+6=х+1, решение которого есть х = -5 – не удовлетворяет выписанному условию. Значит, данное уравнение не имеет решений.
получим уравнение 2х+6=х+1, решение которого есть х = -5 – не удовлетворяет выписанному условию. Значит, данное уравнение не имеет решений.
Ответ: нет решений
Если иррациональное уравнение содержит несколько радикалов. В этом случае для избавления от радикалов уравнение приходится возводить в соответствующую степень несколько раз. При этом предварительно уединяют один из радикалов так, чтобы обе части уравнения стали неотрицательными. Особое внимание следует обратить на правильное нахождение ОДЗ.
Пример 6.
Решить уравнение  .
.
Решение. Запишем уравнение в виде: 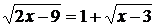 . Так как теперь обе части полученного уравнения неотрицательны, то возведем их в квадрат:
. Так как теперь обе части полученного уравнения неотрицательны, то возведем их в квадрат:
 .
.
Полученное уравнение равносильно исходному. Для его решения рассмотрим систему:
|
|
|

 .
.
Ответ:  .
.
Введение новой переменной в ряде случаев позволяет перейти от иррационального уравнения к рациональному уравнению.
Пример 7.
Решить уравнение  .
.
Решение. Возведение данного уравнения в квадрат привело бы к уравнению четвертой степени, что нерационально. Поэтому запишем уравнение в виде  и введем «новую» переменную:
и введем «новую» переменную:
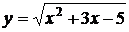 ,
,  .
.
Получим  .
.
Вернемся к «старым» переменным 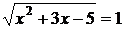 или
или 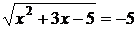 . Второе из полученных уравнений решений не имеет, а решения первого есть числа
. Второе из полученных уравнений решений не имеет, а решения первого есть числа 
Ответ:  .
.
Иногда при решении иррационального уравнения возникает необходимость ввести не одну, а несколько «новых» переменных. Такая ситуация возникает, например, при решении уравнений, содержащих радикалы разных степеней.
Пример 8.
Решить уравнение 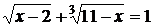 .
.
Решение. Пусть  и
и 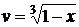 . Тогда
. Тогда  . С другой стороны
. С другой стороны  . Получаем систему
. Получаем систему
 .
.
Решим последнее уравнение системы:

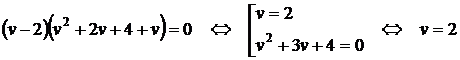 .
.
Получим, что  , а тогда
, а тогда  . По условию
. По условию 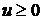 , следовательно исходное уравнение решений не имеет.
, следовательно исходное уравнение решений не имеет.
Ответ: нет решений.
При решении некоторых иррациональных уравнений нахождение области допустимых значений входящих в уравнение неизвестных может существенно облегчить решение уравнения.
|
|
|
При решении иррациональных уравнений бывает полезно воспользоваться монотонностью функций.
Пример 10.
Решить уравнение  .
.
Решение. Один корень данного уравнения 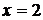 легко найти подбором. Покажем, что других корней нет. Запишем уравнение в виде
легко найти подбором. Покажем, что других корней нет. Запишем уравнение в виде  .
.
По свойству степенных функций функции  и
и  являются возрастающими на промежутке
являются возрастающими на промежутке  , где они обе определены. Поэтому их сумма
, где они обе определены. Поэтому их сумма  на этом промежутке также возрастает, следовательно, она принимает каждое свое значение (в том числе и 6) только один раз. Поэтому других корней нет.
на этом промежутке также возрастает, следовательно, она принимает каждое свое значение (в том числе и 6) только один раз. Поэтому других корней нет.
Ответ: 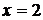 .
.
Определение: Под иррациональным неравенством понимается неравенство, в котором неизвестные величины (или некоторые функции величин) находятся под знаком радикала.
Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе неравенств или совокупности таких систем, не содержащих иррациональных выражений.
Схемы решения:
1) 
2) 
3) 
Пример 1. Решить неравенство
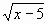 <1.
<1.
Решение.
Обе части неравенства неотрицательны, можно возводить в квадрат, значит,
 , ,  ; ;
| 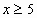 x<6; x<6;
| 
|
Ответ: 
Пример 2. Решить неравенство
|
|
|
 >-1.
>-1.
Решение.
Допустимые значения неравенства:
x+8  x
x 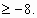
Левая часть неотрицательна, правая – отрицательна, т.е. неравенство выполняется при всех допустимых x.
Ответ: 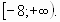
Пример 3. Решить неравенство
 <x.
<x.
Решение.
Допустимые значения неравенства:

Правая часть неравенства может быть отрицательной, но с учётом допустимых значений, обе части неотрицательны. Возводим в квадрат:
 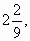

|  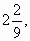
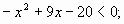
|  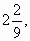

|

Ответ: 
Пример 4. Решить неравенство
 <
<  +5.
+5.
Решение.
Допустимые значения неравенства:
 +61
+61 

Правая часть неравенства может быть отрицательной.
Рассмотрим два случая.
| 1. | 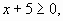 
| 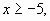  ; ;
| 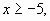 
| |||
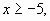 
| 
|
2. 
В этом случае левая часть исходного неравенства неотрицательна, а правая отрицательна. Нет решений.
Ответ: 
Пример 5. Решить неравенство
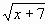 >x+1.
>x+1.
Решение.
Допустимые значения неравенства:

Правая часть неравенства может быть отрицательной.
Рассмотрим два случая.
| 1. | 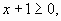 
|  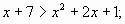
|  
| |||
 
| 
|
2.  т. е. левая часть исходного неравенства неотрицательна, а правая отрицательна. Следовательно, та часть рассматриваемого участка, которая входит в область допустимых значений исходного неравенства, является его решением.
т. е. левая часть исходного неравенства неотрицательна, а правая отрицательна. Следовательно, та часть рассматриваемого участка, которая входит в область допустимых значений исходного неравенства, является его решением.
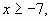
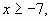

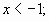

Объединим ответы в первом и во втором случаях:
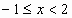 или
или 
Ответ: 
Решать иррациональные неравенства можно, придерживаясь, например, следующего алгоритма:
1.Найти область допустимых значений заданного неравенства.
2.Руководствуясь предложениями о равносильности неравенств, решить заданное неравенство.
3.Из найденных решений отобрать значение переменной, принадлежащее области определения заданного неравенства.
Дата добавления: 2022-12-03; просмотров: 38; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
