Дисконтирование и учет по сложным процентным ставкам
ЛЕКЦИЯ 3 «Современная стоимость денег (дисконтирование)»
Дисконтирование и учет по простым процентным ставкам
В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной наращенной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды Р.
Такая ситуация может возникнуть, например, при разработке условии контракта. Расчет Р на основе заданной величины S необходим и тогда, когда проценты с суммы S удерживаются вперед, т.е. непосредственно при выдаче ссуды. В этих случаях говорят, что сумма Sдисконтируетсяили учитывается,сам процесс начисления процентов и их удержание называют учетом,а удержанные проценты – дисконтом. Необходимость дисконтирования возникает, например, при покупке (учете) банком краткосрочных обязательств (векселей), оплата которых должником произойдет в будущем. Понятие «дисконт» в узком смысле слова употребляется по отношению к ценным бумагам, которые обращаются (т.е.продаются и покупаются) на рынке ценных бумаг, причем их рыночная цена (курсовая стоимость) постоянно изменяется.
Дисконт (от англ. discount ( D ) – разница между ценой некоторой ценной бумаги в настоящий момент и ее ценой на момент погашения (или ценой номинала).
Термин «дисконтирование» употребляется и в более широком смысле – как средство определения любой стоимостной величины, относящейся к будущему, на некоторый, более ранний момент времени. Такой прием часто называют приведениемстоимостного показателя к некоторому, обычно начальному, моменту времени (приведение может быть осуществлено на любой момент времени.)
|
|
|
Дисконтирование (в широком смысле слова) – приведение стоимостных показателей к одному моменту времени.
Величину Р, найденную с помощью дисконтирования, называют современной величиной суммы S, а иногда, в зависимости от контекста, – современной (текущей, приведенной) стоимостью.Современная величина суммы денежных средств является одним из важнейших понятий в количественном анализе финансовых операций. В большинстве случаев именно с помощью дисконтирования, а не наращения учитывается такой фактор, как время. Как мы увидим далее, большинство аналитических методов основывается на определении современной величины платежей.
Следует иметь в виду, что привести стоимость денег можно к любому нужному моменту времени, а не обязательно к началу финансовой операции. Кроме того, с помощью дисконтирования определяют современную стоимость некоторой суммы денег независимо от того, действительно ли совершалась данная операция и можно ли считать дисконтируемую сумму буквально наращенной.
|
|
|
В зависимости от вида используемой процентной ставки применяют два метода дисконтирования:
ü математическое дисконтирование –используется процентная ставка наращения (т.е. ставка ссудного процента) i;
ü банковский (коммерческий) учет – используется учетная процентная ставка d.
Математическое дисконтирование. Математическое дисконтирование представляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды. Решаемая задача в этом случае формулируется так: какую первоначальную сумму денежных средств надо выдать в долг, чтобы получить в конце срока сумму S при условии, что на долг начисляются проценты по ставке i? Решив уравнение относительно Р,находим:
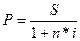
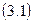
Напомним, что если t – срок ссуды в днях, то n = t/K – срок ссуды в годах (где К – условная продолжительность одного года, которую обычно называют «временной базой» финансовых расчетов и которая может быть различной в финансовой практике разных стран).
Установленная таким способом величина Рявляется современной величиной суммы S,которая будет выплачена спустя nлет.
|
|
|
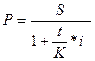
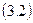
Дробь 1/(1 + n*i)называют дисконтным множителем. Этот множитель показывает, какую долю составляет первоначальная величина долга в окончательной его сумме.
Разность (S – Р) можно рассматривать не только как проценты, начисленные на Р,но и как дисконт (cкидку) с суммы S. Обозначим величину дисконта символом D.
Пример 1. Через 180 дней после подписания кредитного договора клиент банка должен уплатить 310000 рублей. Кредит выдан под 16% годовых. Какова первоначальная сумма долга и величина дисконта при условии, что временная база К равна 365 дням?
Решение:
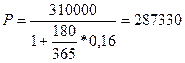 руб.
руб.
Дисконт равен 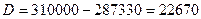 руб.
руб.
Разумеется, дисконт как скидка с конечной суммы долга необязательно определяется через процентную ставку, он может быть установлен по соглашению сторон и в виде абсолютной величины для всего срока.
Банковский (коммерческий) учет (учет векселей). Суть операции заключается в следующем. Банк или иное финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом (со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт. В свою очередь владелец векселя с помощью его учета имеет возможность получить денежные средства, хотя и не в полном объеме, однако раньше указанного на нем срока. При учете векселя применяется банковский (коммерческий)учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.
|
|
|
Размер дисконта (D), или суммы учета равен S*n*d,если d– годовая ставка, то nизмеряется в годах. Таким образом:
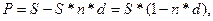
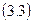
где n – срок от момента учета до даты погашения векселя;
d – дисконтная (учетная) процентная ставка.
Дисконтный множитель здесь равен (1 – n*d).
Учет посредством учетной ставки чаще всего осуществляется при временной базе К= 360 дней, число дней ссуды обычно берется точным.
Пример 2. Тратта (переводной вексель) выдан на сумму 1 млн. рублей с уплатой 17 ноября 2015 года. Владелец векселя учел его в банке 23 сентября 2015 года по учетной ставке 20%. Оставшийся до конца срока период равен 55 дням. Сколько составит полученная при учете сумма (без уплаты комиссионных)?
Решение:
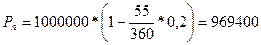 руб.
руб.
Дисконт составит 30600 руб.
Как было показано выше, оба вида процентных ставок применяются для решения сходных задач. Однако для ставки наращения прямой задачей является определение наращенной суммы, а обратной задачей – дисконтирование. Для учетной ставки, наоборот, прямая задача заключается в дисконтировании, обратная – в наращении.
Очевидно, что рассмотренные два метода дисконтирования – по ставке наращения i и учетной ставке d – приводят к разным результатам даже тогда, когда i = d.
Заметим, что учетная ставка отражает фактор времени более жестко. Так, из формулы следует, что при n > 1/d величина дисконтного множителя и, следовательно, суммы Р станет отрицательной. Иначе говоря, при относительно большом сроке векселя учет может привести к нулевой или даже отрицательной сумме Р, что лишено смысла. Например, при d = 20% уже пятилетний срок достаточен для того, чтобы владелец векселя ничего не получил при его учете.
Влияние фактора времени усиливается при увеличении величины ставки. Так, при d = 100% отрицательный результат проявится уже при n > 1. Такая ситуация не возникает при математическом дисконтировании: при любом сроке современная величина платежа здесь больше нуля.
Дисконтирование и учет по сложным процентным ставкам
При изучении простых процентов были рассмотрены математическое дисконтирование и банковский (коммерческий) учет. Первое заключалось в определении Р по значению Sпри заданной ставке процента, второе – при заданной учетной ставке. Дисконтирование позволяет рассчитать современную стоимость будущих поступлений или платежей.
Иногда возникает необходимость применять математическое дисконтирование по сложной ставке процента (используется формула (3.4):
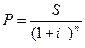
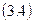
Дробь 1/(1 + i)n называют дисконтным множителем или коэффициентом дисконтирования Такого рода дисконтирование (по ставке сложных процентов) часто требуется при оценке эффективности инвестиционных проектов, связанных с регулярным потоком денежных поступлений в течение длительного периода времени, или в иных случаях, когда речь идет о расчете суммы так называемой финансовой ренты (которая будет рассматриваться на следующей лекции)
Для сравнительной оценки эффективности инвестиционных проектов по стандартной методике, разработанной с учетом международных стандартов, используется показатель так называемой чистой современной (или которая часто приведенной) стоимости (net present value), сокращенно NPV, который представляет собой разность между суммой ожидаемых дисконтированных доходов и суммой первоначальных инвестиций.
Этот показатель NPV рассчитывается по формуле:
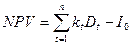
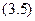
где 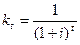 коэффициент дисконтирования в году t; Dt – величина денежных поступлений (доходов) в году t ; n – продолжительность всего периода (выраженная в числе лет), в течение которого ожидаются доходы от реализации инвестиционного проекта; I 0 первоначальная сумма инвестиций, необходимая для реализации проекта. Процентная ставка i – это так называемая безрисковая ставка финансовых вложений (или стандартная «норма прибыли» на вложенный капитал), которая в зарубежных странах часто принимается равной 10% (0,1).
коэффициент дисконтирования в году t; Dt – величина денежных поступлений (доходов) в году t ; n – продолжительность всего периода (выраженная в числе лет), в течение которого ожидаются доходы от реализации инвестиционного проекта; I 0 первоначальная сумма инвестиций, необходимая для реализации проекта. Процентная ставка i – это так называемая безрисковая ставка финансовых вложений (или стандартная «норма прибыли» на вложенный капитал), которая в зарубежных странах часто принимается равной 10% (0,1).
В дополнение к абсолютному показателю NPV рекомендуется также рассчитывать относительный показатель доходности инвестиций (profitability index), сокращенно PI , который рассчитывается по формуле (3.6) и представляет собой отношение суммы дисконтированных доходов к сумме первоначальных инвестиций:
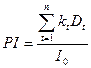
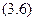
Пример 3.
Требуется сравнить эффективность двух альтернативных инвестиционных проектов (связанных с разработкой и внедрением на рынок новых видов продукции предприятия) с различной суммой первоначальных инвестиций и с различной схемой поступления денежных доходов после реализации проекта.
Известно, что для первого проекта сумма первоначальных инвестиций составит 1000 тыс. руб., а для второго 500 тыс. руб.
Ожидаемые доходы в течение предстоящих пяти лет распределены во времени:
- для первого проекта: равномерно по 300 тыс. в год;
- для второго проекта: неравномерно, в течение первого года проект принесет 100 тыс. руб.; в течение второго года – 150 тыс. руб. а в течение следующих трех лет - по 250 тыс.руб.
По истечении пяти лет оба проекта перестают приносить доход в связи с моральным устареванием разработанных видов продукции и снятием их с производства.
Необходимо рассчитать и сравнить между собой показатели NPV и PI для каждого из двух проектов.
Для удобства расчета значений показателей NPV расчет дисконтированных доходовудобно представлять в виде таблицы (таблица 3.1).
В первом столбце таблицы рассчитываются значения коэффициента дисконтирования для каждого года при i =1. Приведены исходные данные (ожидаемые номинальные доходы) по каждому проекту и рассчитаны значения дисконтированных доходов. В нижней строке таблицы рассчитаны суммы номинальных и дисконтированных доходов.
Таблица 3.1 – Расчет дисконтированных доходов по двум проектам
| год | Коэффициент дисконти-рования | Доходы по первому проекту | Доходы по второму проекту | ||
| Номинальные | Дисконтирован-ные | Номинальные | Дисконтирован-ные | ||
| 0 | 1,0000 | ||||
| 1 | 0,9091 | 300 | 272,73 | 100 | 90,91 |
| 2 | 0,8264 | 300 | 247,93 | 150 | 123,97 |
| 3 | 0,7513 | 300 | 225,39 | 250 | 187,83 |
| 4 | 0,6830 | 300 | 204,90 | 250 | 170,75 |
| 5 | 0,6209 | 300 | 186,28 | 250 | 155,23 |
| Итого (сумма) | 1500 | 1137,24 | 1000 | 728,69 | |
В таблице 3.1. мы видим что сумма номинальных доходов по первому проекту больше (1500>1000), но ровно настолько же больше и сумма первоначальных инвестиций, т.е. без учета дисконтирования прибыль (доходы минус затраты) по обоим проектам одинаковая: 1500-1000=1000-500=500 (тыс.руб.). В то же время отношение получаемых доходов к затратам (рентабельность) по второму проекту больше: 1500/1000 = 1,5 (150%), 1000/500= 2 (200%).
С учетом дисконтирования получается другая картина:
По первому проекту NPV= 1137,24-1000= 137,24 ; PI = 1137,24/1000 = 113,7%
По второму проекту NPV =728,69 – 500= 228,69; PI = 728,69/500 = 145,7%
В любом случае второй проект выгоднее первого.
Для случаев, когда проценты начисляются mраз в году, формула (3.4) преобразуется в формулу (3.7):
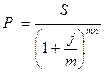
где j – годовая (номинальная) процентная ставка, m – число начислений процентов в течение одного года, n – продолжительность всего срока денежных поступлений (число лет).
Величину Р, полученную путем дисконтирования некоторой суммы денежных средств S, называют современной величиной, или современной стоимостью S. Современная стоимость может быть рассчитана на любой момент до выплаты суммы S. Разность S-P, в случае когда Р определено дисконтированием, называют дисконтом и обозначают через D.
 | |||
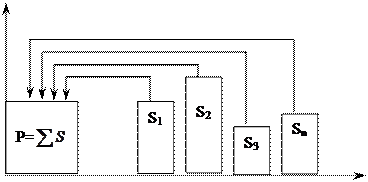 | |||
настоящее будущее время
Рис. 5. Схема дисконтирования
Современная (дисконтированная) величина денежной суммы – одна из важнейших характеристик, применяемых в финансовом анализе.Кратко остановимся на некоторых ее формальных свойствах:
ü чем выше ставка процента, тем интенсивнее дисконтирование при всех прочих равных условиях;
ü значение дисконтного множителя уменьшается с ростом величины m;
ü с увеличением срока при прочих равных условиях размер современной стоимости убывает.
Операции дисконтирования используются:
ü в инвестиционном анализе (при сравнительной оценке эффективности разных инвестиционных проектов);
ü в финансовом менеджменте (при оценке финансовых вложений в ценные бумаги или иные финансовые активы, приносящие доход в будущем);
ü при оценке выгодности лизинговых и кредитных договоров.
Дата добавления: 2022-12-03; просмотров: 19; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
