Построение эпюр внутрениих усилий
С.И. Оплетаев, В.А. Трубин
Построение эпюр внутренних усилий
Курган - 2008
С.И. Оплетаев, В.А. Трубин
Построение эпюр внутренних усилий
Методические указания
Курган - 2008
УДК 539.3
Оплетаев С.И, Трубин В.А. Построение эпюр внутренних усилий: Методические указания.– Курган: Изд-во КГСХА, 2008.- 23 с
Рецензент: В.С. Зуев, кандидат технических наук, доцент Курганской сельскохозяйственной академии.
Методические указания подготовлены в соответствии с государственным образовательным стандартом высшего образования по специальностям 110301 - Механизация сельского хозяйства, 270102 - Промышленное и гражданское строительство и 110302 – Электрификация и автоматизация сельского хозяйства.
Методические указания рассмотрены и одобрены на заседании кафедры теоретической механики (протокол № 4 от 28 декабря 2007 г.), рекомендованы к изданию методической комиссией факультета механизации сельского хозяйства (протокол № 5 от 19 марта 2008 г.).
© ФГОУ ВПО «Курганская государственная сельскохозяйственная академия имени Т.С. Мальцева», 2008
Содержание
| Введение ……………………………………………………………… | 4 |
| 1 Внутренние усилия и метод их определения (метод сечений)…………………………………………………. | 4 |
| 2 Построение эпюр продольных сил при растяжении (сжатии) ………………………………………… | 8 |
| 3 Построение эпюр крутящих моментов при кручении ……………...................................................................... | 11 |
| 4 Построение эпюр поперечных сил и изгибающих моментов при плоском поперечном изгибЕ ………... | 14 |
| ЗаключениЕ ………………………………………………………. | 21 |
| литература …………………………………………….................... | 22 |
|
|
|
Введение
Определение внутренних усилий и построение их эпюр является одной из основных задач курса «Сопротивление материалов». Приемом, позволяющим определять внутренние усилия, является метод сечений. В учебниках по сопротивлению материалов показаны два основных способа определения величин внутренних силовых факторов и построения их эпюр.
При первом способе рассматривается сечение стержня, положение которого определяется текущим значением координаты, и составляется аналитическое выражение искомого силового фактора. Эпюра при этом является графиком полученной зависимости. Способ позволяет математически точно описать закономерности изменения внутренних усилий, но является достаточно трудоемким.
Второй способ представляет собой сокращенный вариант первого и основан на знании основных закономерностей поведения эпюр. Внутренние усилия определяются в характерных сечениях стержня. К таким относятся сечения, расположенные в начале и в конце каждого силового участка, а также некоторые промежуточные, в которых внутренние усилия достигают экстремальных значений.
|
|
|
1 Внутренние усилия и метод их определения
(метод сечений)
В любом элементе конструкции под действием внешних нагрузок возникают внутренние усилия. Определим их с помощью метода сечений. Рассечем стержень (рисунок 1, а) в интересующем нас месте плоскостью I, совпадающей с плоскостью поперечного сечения стержня. В полученном поперечном сечении в общем случае действует шесть внутренних усилий: 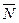 ,
, 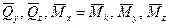 (рисунок 1, б, в). Усилия
(рисунок 1, б, в). Усилия 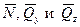 представляют собой составляющие главного вектора, а
представляют собой составляющие главного вектора, а 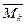 ,
, 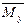 и
и 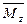 - составляющие главного момента системы внутренних сил.
- составляющие главного момента системы внутренних сил.
Сила 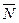 , нормальная к сечению, и совпадающая с продольной осью x стержня, называется продольной силой и вызывает деформацию растяжения (сжатия). Силы
, нормальная к сечению, и совпадающая с продольной осью x стержня, называется продольной силой и вызывает деформацию растяжения (сжатия). Силы 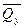 и
и 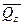 , лежащие в плоскости поперечного сечения и совпадающие с осями y и z, называются поперечными силами и вызывают деформацию сдвига.
, лежащие в плоскости поперечного сечения и совпадающие с осями y и z, называются поперечными силами и вызывают деформацию сдвига.
Момент 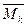 , действующий относительно продольной оси x в плоскости сечения, называется крутящим и вызывает деформацию кручения. Моменты
, действующий относительно продольной оси x в плоскости сечения, называется крутящим и вызывает деформацию кручения. Моменты 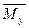 и
и 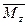 , действующие относительно осей y и z в плоскостях, перпендикулярных сечению, называются изгибающими и вызывают деформацию изгиба.
, действующие относительно осей y и z в плоскостях, перпендикулярных сечению, называются изгибающими и вызывают деформацию изгиба.
|
|
|
Запишем уравнения равновесия для правой части стержня (рисунок 1, б):
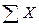 = N ± P4x ± P5x± …± Pix = 0
= N ± P4x ± P5x± …± Pix = 0
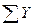 = Qy ± P4y ± P5y ± …± Piy = 0
= Qy ± P4y ± P5y ± …± Piy = 0
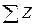 = Qz ± P4z ± P5z ± …± Piz = 0
= Qz ± P4z ± P5z ± …± Piz = 0
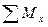 = Mk ± Mx(
= Mk ± Mx( 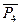 ) ± Mx(
) ± Mx( 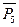 ) ± … ± Mx(
) ± … ± Mx( 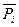 ) =0 , (1)
) =0 , (1)
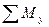 = My ± My(
= My ± My( 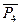 ) ± My(
) ± My( 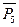 ) ± … ± My(
) ± … ± My( 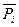 ) =0
) =0
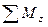 = Mz ± Mz(
= Mz ± Mz( 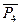 ) ± Mz(
) ± Mz( 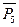 ) ± … ± Mz(
) ± … ± Mz( 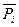 ) =0
) =0

Рисунок 1 – Определение внутренних усилий
где Pix , Piy , Piz – проекции внешних сил на оси x, y, z ;
Mx( 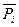 ), My(
), My( 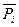 ), Mz(
), Mz( 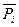 ) – моменты внешних сил относительно осей x, y, z.
) – моменты внешних сил относительно осей x, y, z.
Аналогичным образом можно рассмотреть равновесие левой части стержня (рисунок 1, в) и записать систему уравнений равновесия. Решив систему уравнений (1) для правой части и аналогичную систему для левой части стержня, получим величины внутренних усилий, действующих в поперечном сечение стержня.
Итак, для нахождения внутренних усилий методом сечений необходимо:
1. Рассечь стержень поперечным сечением в том месте, где определяем внутренние усилия.
2. Отбросить одну из частей.
3. Заменить действие отброшенной части на оставшуюся (отсеченную) внутренними усилиями.
|
|
|
4. Уравновесить отсеченную часть, т. е. составить уравнения равновесия и решить их.
Таким образом, абсолютная величина любого из шести внутренних усилий полностью определяется внешними нагрузками, действующими на отсеченную часть стержня.
2 Построение эпюр продольных сил при растяжении (сжатии)
Эпюрой называется график изменения внутреннего усилия по длине стержня. На эпюре указываются величины и знаки внутренних усилий. Знаки показывают направления этих усилий.
Продольная сила N при растяжении считается положительной (увеличивается длина стержня), т.е. когда она направлена от сечения, а при сжатии – отрицательной (длина стержня уменьшается), т.е. направленной на сечение (рисунок 2).

N > 0 N < 0
Рисунок 2 – Правило знаков для продольных сил
С учетом правила знаков и системы (1) продольную силу в поперечном сечении стержня можно найти по формуле:
N = ± P4x ± P5x ± … ± Pix (2)
Таким образом, продольная сила N численно равна алгебраической сумме проекций на продольную ось x всех внешних сил, действующих на отсеченную часть стержня.
Построение эпюры первым способом позволяет выявить общие закономерности поведения эпюры продольных сил:
1. На участках стержня, где нет распределенной нагрузки, продольная сила постоянна.
2. На участках стержня, где действует равномерно распределенная осевая нагрузка, продольная сила изменяется по линейной зависимости на величину, равную равнодействующей от распределенной на этом участке нагрузки.
3. В сечении стержня, где приложена сосредоточенная осевая нагрузка, на эпюре имеется скачок, равный по величине этой нагрузке.
4. В сечении, где начинается или заканчивается действие распределенной нагрузки, на эпюре имеется излом.
Пример 1. Построить эпюру продольных сил для стержня, изображенного на рисунке 3.
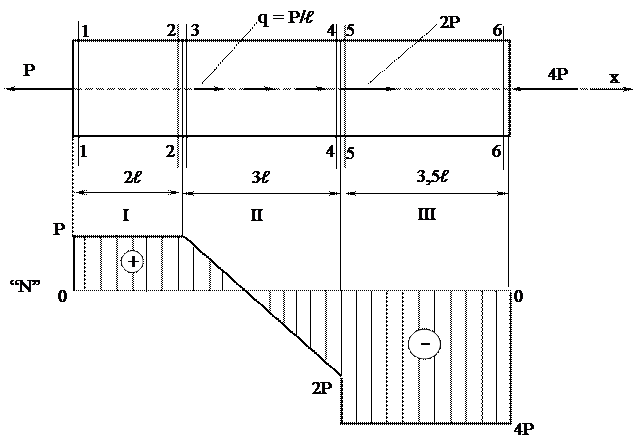
Рисунок 3 – Построение эпюры продольных сил.
Стержень имеет три силовых участка. Определим продольную силу в характерных сечениях:
N1 = N2 = +P = const (N > 0, т.к. внешняя нагрузка P вызывает растяжение отсеченной части стержня);
N3 = +P;
N4 = P – q × 3  = -2P;
= -2P;
N5 = N6 = P – q × 3  – 2P = -4P.
– 2P = -4P.
Строим эпюру продольных сил. Для этого проведем нулевую линию, параллельную оси стержня, и отложим полученные значения перпендикулярно к нулевой линии с учетом их знаков. Полученные ординаты соединим прямыми линиями. Эпюра построена.
Если стержень закреплен одним концом, то нет необходимости в определении опорных реакций. Расчет следует вести со свободного конца стрежня.
Рекомендуется выполнять расчеты, рассматривая равновесие, например, левой части стержня на каждом участке. Для контроля правильности решения следует рассмотреть равновесие правой части стрежня на одном – двух участках. При одинаковых значениях продольной силы (по модулю и знаку) расчет можно считать верным.
3 Построение эпюр крутящих моментов при кручении
Стержни, работающие на кручение, называются валами.
Из системы уравнений (1) следует, что крутящий момент в любом поперечном сечении вала численно равен алгебраической сумме всех внешних скручивающих моментов, действующих на отсеченную часть вала относительно продольной оси:
Mk = ± Mx ( 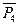 ) ± Mx (
) ± Mx ( 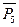 ) ± … ± Mx (
) ± … ± Mx ( 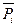 ) (3)
) (3)
Общепринятого правила знаков, показывающих направление крутящего момента, не существует. Примем следующее правило знаков: если при взгляде на поперечное сечение со стороны отброшенной части вала крутящий момент в сечении будет направлен против часовой стрелки, то он считается положительным, и наоборот (рисунок 4).
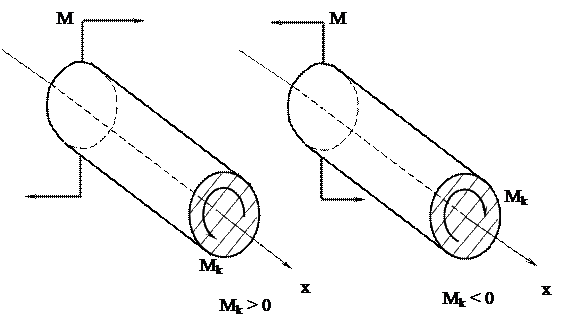
Рисунок 4 – Правило знаков для крутящих моментов
Построение эпюр крутящих моментов и продольных сил имеет много сходства потому, что сосредоточенный скручивающий момент аналогичен сосредоточенной осевой нагрузке, а распределенный момент - распределенной нагрузке.
Поэтому общие закономерности поведения эпюр крутящих моментов и продольных сил аналогичны:
1. На участке вала, где нет распределенной моментной нагрузки, крутящий момент постоянен.
2. На участке вала, на котором действует равномерно распределенный скручивающий момент, крутящий момент изменяется линейно на величину, равную результирующей действующего на этом участке момента.
3. В сечении вала, где приложен сосредоточенный внешний скручивающий момент, на эпюре имеется скачок, равный по величине этому моменту.
4. В сечении, где начинается или заканчивается действие равномерно распределенного скручивающего момента, на эпюре имеется излом.
Как правило, скручивающие моменты подводятся к валам в местах крепления шестерен, шкивов, звездочек и т.п., поэтому эти моменты можно считать сосредоточенными. Кроме сосредоточенных моментов валы могут быть нагружены и распределенными моментами.
Пример 2. Построить эпюру крутящих моментов для вала, изображенного на рисунке 5.
Вал имеет четыре силовых участка. Определим в характерных сечениях крутящий момент:
Mk1 = Mk2 = 0
Mk3 = Mk4 = -2M (Mk < 0, т.к. в рассматриваемых сечениях он направлен по ходу часовой стрелки);
Mk5 = - 2M + 3M = +M;
Mk6 = -2M + 3M + m×2  = + 3M;
= + 3M;
Mk7 = Mk8 = - 2M + 3M + m×2  +M = +4M
+M = +4M
Строим эпюру крутящих моментов. Параллельно оси стержня проводим нулевую линию и откладываем полученные значения перпендикулярно ей с учетом их знаков. Полученные ординаты соединим прямыми линиями. Эпюра построена.
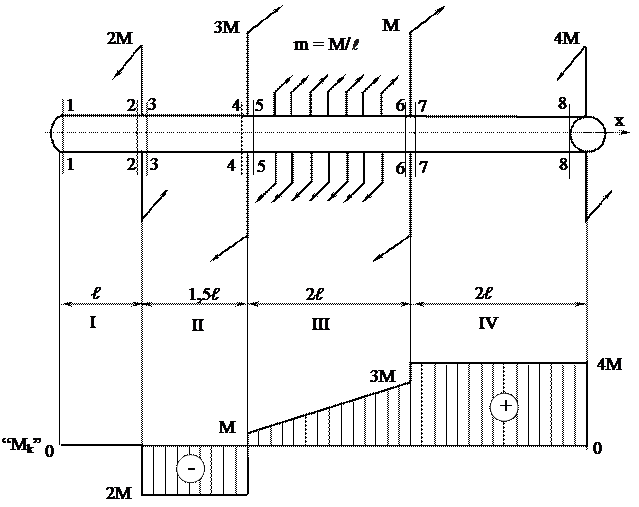
Рисунок 5 – Построение эпюры крутящих моментов
Следует помнить, что вид эпюры не зависит от выбора отсеченной и отброшенной части. Поэтому, рассмотрев равновесие левой части вала на каждом силовом участке, для проверки правильности решения нужно рассмотреть равновесие правой части вала на одном-двух участках. Если результаты расчета крутящего момента совпадут, то расчет можно считать верным.
4 Построение эпюр поперечных сил и изгибающих моментов при плоском поперечном изгибе
При плоском поперечном изгибе в поперечных сечениях балки (так называют стержни, работающие на изгиб) возникают два внутренних усилия: поперечная сила Qy и изгибающий момент Mz (или Qz и My). Если при изгибе поперечная сила равна нулю, то такой изгиб называется чистым.
Принято считать, что при чистом изгибе все слои (волокна) элемента балки (рисунок 6) длиной dx после деформации искривляются, имея общий центр кривизны О. В результате волокна, расположенные на уровне центра тяжести сечения и совпадающие с одной из главных осей инерции, не меняют своей длинны. В поперечном сечении они образуют нейтральную линию (Н.Л.). Все остальные волокна или увеличивают свою длину (растягиваются) или уменьшают ее (сжимаются). Положение сжатых и растянутых волокон важно знать потому, что эпюры изгибающих моментов строятся со стороны сжатых или растянутых волокон.
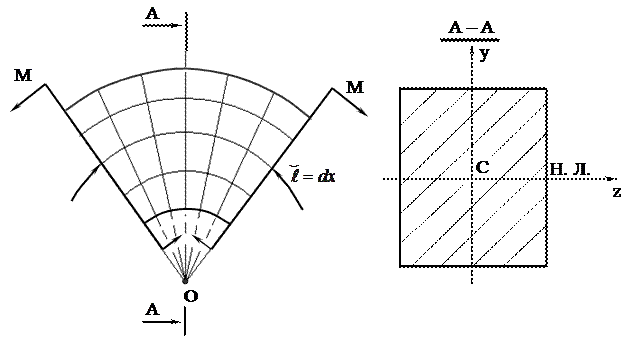
Рисунок 6 – Модель поведения элемента балки при чистом изгибе
Из системы уравнений (1) следует, что поперечная сила в любом поперечном сечении балки численно равна алгебраической сумме проекций всех внешних сил, приложенных к отсеченной части, на ось, перпендикулярную продольной оси балки:
Qy = ± P4y ± P5y ± … ± Piy
(Qz = ± P4z ± P5z ± … ± Piz) (4)
Поперечная сила в сечении балки считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз; т. е. если внешняя сила стремится вращать отсеченную часть балки относительно центра тяжести проведенного сечения по ходу часовой стрелки; и отрицательной, если в противоположном направлении (рисунок 7, а).
Также из системы (1) следует, что изгибающий момент в любом поперечном сечении балки численно равен алгебраической сумме всех действующих на отсеченную часть моментов внешних сил (включая сосредоточенные моменты), вычисленных относительно центра тяжести сечения:
Mz = ± Mz( 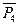 ) ± Mz(
) ± Mz( 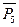 ) ±… ± Mz(
) ±… ± Mz( 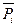 )
)
(My = ± My( 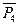 ) ± My(
) ± My( 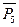 ) ±… ± My(
) ±… ± My( 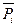 )) (5)
)) (5)
Изгибающий момент в сечении балки считается положительным, если в рассматриваемом сечении балка изгибается выпуклостью вниз, т.е. сжаты верхние волокна, а нижние растянуты; и отрицательным – в противоположном случае (рисунок 7, б). Для нахождения знака нужно мысленно жестко закрепить отсеченную часть балки в проведенном сечении и затем определить, как будет изгибаться эта часть под действием внешней нагрузки.
Между изгибающим моментом М, поперечной силой Q и интенсивностью распределенной нагрузки q существуют дифференциальные зависимости:
q = dQ/dx
Q = dM/dx (6)

Рисунок 7 – Правила знаков для поперечных сил и изгибающих моментов
Они определяют основные закономерности поведения эпюр внутренних усилий при изгибе:
1. На участке, где нет распределенной нагрузки, поперечная сила постоянна (линия эпюры параллельна нулевой линии), а изгибающий момент изменяется по линейной зависимости (прямая наклонена к нулевой линии).
2. На участке с равномерно распределенной нагрузкой поперечная сила изменяется линейно на величину, равную результирующей распределенной на участке нагрузки, а изгибающий момент – по параболической зависимости.
3. Если на участке действия распределенной нагрузки эпюра поперечных сил не пересекает нулевую линию, то изгибающийся момент на этом участке изменяется монотонно, без экстремумов.
4. Если на участке действия распределенной нагрузки эпюра поперечных сил пересекает нулевую линию, то в месте пересечения на эпюре изгибающих моментов будет экстремум: максимум (поперечная сила меняет знак с плюса на минус) или минимум (поперечная сила меняет знак с минуса на плюс).
5. В сечении, где к балке приложена сосредоточенная нагрузка, на эпюре поперечных сил будет скачок, равный величине этой нагрузки.
6. В сечении, где на балку действует внешний сосредоточенный момент, на эпюре изгибающих моментов будет скачок, равный величине этого момента.
7. Изгибающий момент в конце силового участка Mzk равен сумме изгибающего момента в начале силового участка Mzн и площади эпюры поперечных сил Sэп.Q на этом участке:
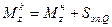 (7)
(7)
Перечисленные закономерности являются и правилами проверки правильности построения эпюр.
Пример3. Построить эпюры поперечных сил Qy и изгибающих моментов Mz для балки, изображенной на рисунке 8.
Определим реакции в опорах.
SMA = P × 0,5  – M – q × 6
– M – q × 6  × 5
× 5  + RB × 6
+ RB × 6  = 0,
= 0,
откуда RB = 5q  ;
;

Рисунок 8 – Построение эпюр внутренних усилий при изгибе
SMВ = P × 7  – RA × 6
– RA × 6  - M + q × 4
- M + q × 4  × 2
× 2  - q × 2
- q × 2  ×
×  = 0,
= 0,
откуда RA = 3q  ;
;
Проверка: SY = -2q  + RA - q× 6
+ RA - q× 6  + RB = 0.
+ RB = 0.
Учитывая правила знаков, определим внутренние усилия в характерных сечениях балки:
Qy1 = Qy2 = -P = -2q  ;
;
Qy3 = Qy4 = Qy5 = Qy6 = Qy7 = -P +RA = +q  ;
;
Qy8 = -P + RA - q× 4  = -3q
= -3q  ;
;
Qy9 = -P + RA - q× 4  + RB = +2q
+ RB = +2q  ;
;
Qy10 = -P + RA - q× 6  + RB = 0.
+ RB = 0.
Mz1 = 0;
Mz2 = Mz3 = -P × 0,5  = -q
= -q  2;
2;
Mz4 = -P × 1,5  + RA ×
+ RA ×  =0;
=0;
Mz5 = -P × 1,5  + RA ×
+ RA ×  + M = +q
+ M = +q 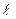 2;
2;
Mz6 = Mz7 = -P × 2,5  + RA × 2
+ RA × 2  + M = +2q
+ M = +2q  2;
2;
Mz8 = Mz9 = -P × 6,5  + RA × 6
+ RA × 6  + M – q × 4
+ M – q × 4 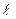 × 2
× 2 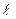 = -2q
= -2q  2;
2;
Mz10 = -P × 8,5  + RA × 8
+ RA × 8  + M – q × 6
+ M – q × 6 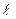 × 3
× 3 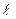 + RB × 2
+ RB × 2 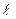 = 0.
= 0.
Отложенные в масштабе значения поперечных сил напротив соответствующих сечений соединим на участках I, II и III прямыми, параллельными нулевой линии, а на участке IV и V – прямыми, наклонными к нулевой линии. При построении эпюры Mz значения ординат изгибающих моментов на участках I, II и III соединим прямыми, наклонными к нулевой линии, а на участках IV и V – квадратичными параболами.
Эпюра может быть построена как на сжатых волокнах (рисунок 8, б), так и на растянутых (рисунок 8, в). В первом случае положительные значения моментов откладываются выше нулевой линии – парабола направлена выпуклостью навстречу распределенной нагрузке (правило «зонта»). В другом случае положительные значения моментов откладываются ниже нулевой линии – парабола направлена вогнутостью навстречу распределенной нагрузке (правило «податливой гибкой пленки»).
На участке IV определим экстремальное значение изгибающегося момента. Для этого найдем координату x сечения, в котором Qy = 0. Она определяется из подобия треугольников эпюры Qy на IV участке (рисунок 8, а):
q  /x = 3 q
/x = 3 q  /(4
/(4  - x), откуда x =
- x), откуда x =  ; тогда экстремальный момент на IV участке:
; тогда экстремальный момент на IV участке:
Mz11 = -P × 3,5  + RB × 3
+ RB × 3  + M – q ×
+ M – q ×  ×0,5
×0,5  = +2,5 q
= +2,5 q  2.
2.
Полученные эпюры следует проверить в соответствии с пунктами 1…7 основных закономерностей поведения эпюр внутренних усилий при изгибе. Подробно рассмотрим проверку, выполняемую по формуле (7):
Mz1 = 0;
Mz2 = Mz3 = Mz1 + 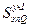 = 0 – 2q
= 0 – 2q 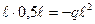 ;
;
Mz4 = Mz3 + 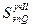 = – q
= – q 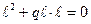 ;
;
Mz5= Mz4 + M = 0 + q 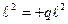 ;
;
Mz6 = Mz7 = Mz5 + 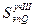 = q
= q 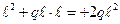 ;
;
Mz8 = Mz9 = Mz7 + 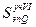 =
= 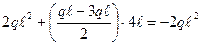 ;
;
Mz10 = Mz9 + 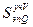 = -
= - 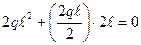 ;
;
Mz11 = Mz7 + 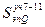 =
= 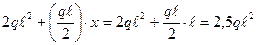 .
.
Таким образом, эпюры поперечных сил и изгибающих моментов построены верно.
Заключение
Наибольшее затруднение у студентов при решении задач по сопротивлению материалов вызывает определение внутренних усилий и построение их эпюр. Рассматриваемый в данных методических указаниях способ определения внутренних усилий в характерных сечениях отличается краткостью, лаконичностью, не требует составления аналитических выражений, что существенно сокращает объем вычислений. Построенные эпюры должны быть проверены с использованием основных закономерностей их поведения (правил проверки правильности построения). Таким образом, используя предлагаемый алгоритм, студент имеет возможность самостоятельно контролировать ход расчета и построения эпюр внутренних усилий.
литература
1. Александров А. В., Потапов В.Д., Державин Б.П. Сопротивление материалов: Учеб. для вузов. – М.: Высш. шк., 1995. – 560с.:ил.
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов: Учеб. для техн. Вузов – 5-е изд., 1989. – 624с.: ил.
3. Тютрин С.Г. Построение эпюр внутренних силовых факторов: Учебное пособие. – Курган: Изд-во Курганского государственного университета. 1997. – 51с.
Построение эпюр внутрениих усилий
Методические указания
Составители:
Сергей Иванович Оплетаев
Владимир Александрович Трубин
ЛИЦЕНЗИЯ ЛР № 021298 от 18 июня 1998 г.
|
Дата добавления: 2022-11-11; просмотров: 128; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
