Производная сложной функции. Полная производная.
Наибольшее и наименьшее значение функции в замкнутой области. Глобальный экстремум.
Постановка задачи. Пусть функция z = f( x, y) определена и непрерывна в ограниченной замкнутой области D. Тогда она достигает в некоторых точках области D, в том числе и на её границах, своего наибольшего и наименьшего значений (т.н. глобальный экстремум). При этом наибольшее и(или) наименьшее значения могут не совпадать со значениями максимумов и минимумов (т.н. локальными экстремумами) внутри области D.
Для отыскания наибольшего и наименьшего значений в ограниченной области D воспользуемся следующим алгоритмом.
Алгоритм нахождения наибольшего и наименьшего значения.
1)_Находим стационарные точки функции z = f( x, y)
2)_ Вычисляем значение функции в стационарных точках внутри области D (те точки, которые не входят в область D, отбрасываем)
3)_ Находим стационарные точки на границе области D
4)_ Вычисляем значение функции в стационарных точках на границе области D (отбрасываем те точки, которые не входят в область D). Вычисляем значение функции в «подозрительных» точках на границе области D
5)_Из полученных значений z выбираем наименьшие и наибольшие значения
Пример. Найти наибольшее и наименьшее значения функции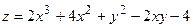 
в замкнутой области, ограниченной линиями: 
, 
.
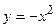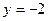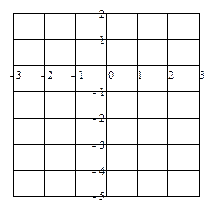Решение.
1) Находим производные первого порядка.
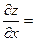6х2 + 8х – 2у 
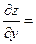2у – 2х
|
|
|
|
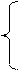
6х2 + 8х – 2у = 0; 3х2 + 4х – у = 0;
2 у – 2х = 0, у = х,
х1 = 0, у1 = 0 и х2 = –1, у2 = –1.
Получаем стационарные точки: _М1(0;0) и М2(-1;-1)_________
2) Вычисляем значение функции в стационарных точках внутри области D. Для наглядности нарисуем область D в декартовой системе координат Оху (см. рис).
Обе стационарные точки принадлежат области D .
z(0;0) = 2*0 + 4*0 + 0 – 2*0*0 – 4 = – 4 ;
z(-1;-1) = 2*(-1)3 + 4*(-1)2 + (-1)2 – 2*(-1) *(-1) – 4 = – 2 + 4 + 1 – 2 – 4 = – 3.
3) Находим стационарные точки на границе области.
а) исследуем границу 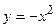области D.
Подставляем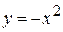 
в исходную функцию:
z = 2 х3 + 4 х2 + (– х2)2 – 2х *(–х2) – 4 = 2 х3 + 4 х2 + х4 + 2 х3 – 4 = х4 + 4 х3 + 4 х2 – 4 .
Находим стационарные точки
z ' = 4 х3 + 12 х2 + 8 х = 0, отсюда: х (х2 + 3 х + 2) = 0,
Тогда: х1 = 0, у1 = 0; х2 = – 1, у2 = – 1; х3 = – 2, у3 = – 4 (подставили значения xi в равенство у = – х2). Получили уже найденные ранее стационарные точки М1(0;0) и М2(-1;-1).
б) исследуем границу 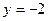области D.
Подставляем у = – 2 в исходную функцию:
z = 2 х3 + 4 х2 + (– 2)2 – 2х *(–2) – 4 = 2 х3 + 4 х2 + 4 + 4 х – 4 = 2 х3 + 4 х2 + 4 х .
|
|
|
Находим стационарные точки
z ' = 6 х2 + 8 х + 4 = 0, отсюда: 3х2 + 4 х + 2 = 0, дискриминант отрицательный, стационарных точек нет.
4) Вычисляем значение функции в стационарных точках на границе области D.
z(0;0) = – 4 (найдено ранее)
z(-1;-1) = – 3 (найдено ранее)
Точка с координатами х3 = – 2, у3 = – 4 нам не нужна – не входит в область D (см. рис).
«Подозрительные» точки – это точки пересечения кривых, образующих область D :
у = – х2, у = – 2 . Координаты точек их пересечения: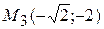 
и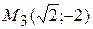 
. Значение функции в этих точках:
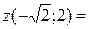- 3,314
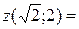19,314
5)_Из полученных значений z выбираем наименьшие и наибольшие значения:
z(0;0) = – 4 - минимум
z(-1;-1) = – 3
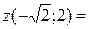– 3,314
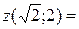19,314 - максимум
Глобальный экстремум. 
Точки, в которых функция принимает наибольшее или наименьшее значение в ограниченной замкнутой области, называют точками глобального экстремума.
Производная сложной функции. Полная производная.
аргументов.
Дата добавления: 2022-11-11; просмотров: 86; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!