П4. Свойства производных. Вычисление производных.
Тема 2. Производная и её приложения.
Производная функции.
П1. Задачи, приводящие к понятию производной.
а) Прямолинейное движение материальной точки.
Пусть материальная точка движется прямолинейно по закону 
 . Вычислим её среднюю скорость. Из физики известно, что
. Вычислим её среднюю скорость. Из физики известно, что  , где
, где 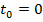 начальный момент времени,
начальный момент времени,  - конечный момент времени,
- конечный момент времени, 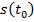 - путь пройденный телом до момента времени
- путь пройденный телом до момента времени 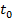 ,
, 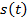 - путь пройденный телом до момента времени
- путь пройденный телом до момента времени 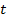 . Средняя скорость слабо характеризует движение. Для более точной характеристики вычислим мгновенную скорость (скорость за минимальный промежуток времени), то есть скорость при
. Средняя скорость слабо характеризует движение. Для более точной характеристики вычислим мгновенную скорость (скорость за минимальный промежуток времени), то есть скорость при  . Итак,
. Итак,

б) Протекание тока в электрической цепи.
Пусть количество электричества (в кулонах), протекающее через поперечное сечение проводника, изменяется по закону 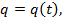
 . Вычислим среднюю силу тока в данной цепи. Из физики известно, что
. Вычислим среднюю силу тока в данной цепи. Из физики известно, что  , где
, где 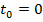 начальный момент времени,
начальный момент времени,  - конечный момент времени,
- конечный момент времени,  - количество электричества, протекшее через поперечное сечение проводника до момента времени
- количество электричества, протекшее через поперечное сечение проводника до момента времени 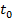 ,
, 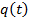 - количество электричества, протекшее через поперечное сечение проводника до момента времени
- количество электричества, протекшее через поперечное сечение проводника до момента времени 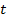 . Средняя сила тока слабо характеризует процесс. Для более точной характеристики вычислим мгновенную силу тока (силу тока за минимальный промежуток времени), то есть силу тока при
. Средняя сила тока слабо характеризует процесс. Для более точной характеристики вычислим мгновенную силу тока (силу тока за минимальный промежуток времени), то есть силу тока при  . Итак,
. Итак,

П2. Понятие производной.
При решений многих задач возникают пределы, подобные пределам из п1. Подробное их рассмотрение привело к появлению понятия производной.
|
|
|
Опр. Пусть задана функция  и пусть
и пусть 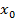 некоторая точка из интервала
некоторая точка из интервала 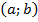 . Предел
. Предел
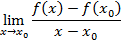
называется производной функции  в точке
в точке 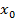 и обозначается
и обозначается  .
.
Итак, по определению

Опр. Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке.
Опр. Функция, имеющая производную в любой точке, называется дифференцируемой.
Опр. Процесс нахождения производной называется дифференцированием.
Запишем определение производной в другом виде: пусть 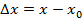 ; так как
; так как 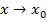 , то
, то  ; причем
; причем  . Тогда определение производной примет вид:
. Тогда определение производной примет вид:
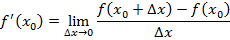
Заменим 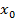 на
на  и получим ещё одно определение производной:
и получим ещё одно определение производной:

Опр. Производная это предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Существуют несколько способов записи производной, например,

Возвращаясь к задачам, рассмотренным в п1. можно отметить, что:
а)  - мгновенная скорость в момент времени
- мгновенная скорость в момент времени 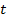 есть производная от пути по времени;
есть производная от пути по времени;
б)  - мгновенная сила тока в момент времени
- мгновенная сила тока в момент времени 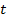 есть производная от количества электричества по времени.
есть производная от количества электричества по времени.
П3. Вычисление производной по определению.
Чтобы вычислить производную функции  по определению нужно:
по определению нужно:
|
|
|
1) выписать  ;
;
2) составить  ;
;
3) составить и упростить 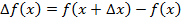 ;
;
4) составить и упростить 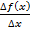 ;
;
5) вычислить  .
.
Например, вычислим производные функций по определению:
а)  , где
, где  ; б)
; б) 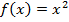 .
.
Решение:
а) 1) 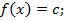
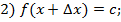

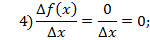

Значит, 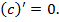
б) 1) 
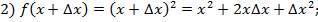
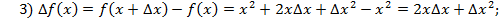


Значит, 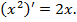
Задание 1. Вычислить производные следующих функций по определению:
а)  ; б)
; б) 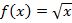 , в)
, в) 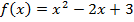 .
.
Итак, теперь мы знаем производные некоторых функций:
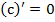
 ;
; 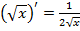 ;
; 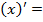 1;
1; 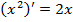 .
.
Аналогично могут быть получены производные следующих функций:
 ;
;  ,
, 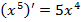 .
.
п4. Свойства производных. Вычисление производных.
Если функции  и g
и g 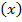 дифференцируемы, то имеют место формулы
дифференцируемы, то имеют место формулы



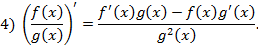
Например, вычислим производные функций:
а)  ;
;
б)  .
.
Решение:
а) 
 .
.
б) 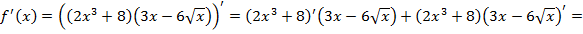

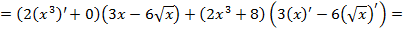

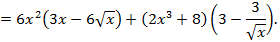
Задание 2. Вычислить производные функций:
а) 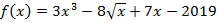 ; б)
; б)  ; в)
; в) 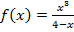 ; г)
; г) 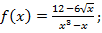
д)  ; е)
; е)  ; ж)
; ж) 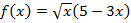 .
.
Домашнее задание.
Задание 1. Выписать и выучить формулы сокращённого умножения: 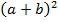 ,
, 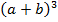 ,
,  ,
, 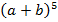 ,
,  ,
,  ,
, 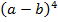 ,
,  ,
, 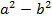 ,
, 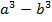 ,
, 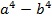 ,
,  .
.
Задание 2. Вычислить производные функций по определению:
а)  ; б)
; б) 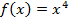 ; в)
; в)  ; г)
; г) 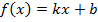 , где
, где 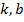 - некоторые константы, д)
- некоторые константы, д) 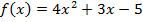 .
.
Задание 3. Вычислить производные функций:
а)  ; б)
; б)  ; в)
; в) 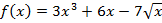 ;
;
г) 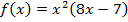 ; д)
; д) 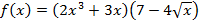 ; е)
; е)  ; ж)
; ж) 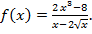
Дата добавления: 2022-07-16; просмотров: 52; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
