Одношаговые методы решения обыкновенного дифференциального уравнения
Рассмотрим наиболее распространенные численные методы решения задачи Коши (6.1), называемые методами Рунге-Кутта. Пусть  – заданное положительное число (шаг). Построим на отрезке
– заданное положительное число (шаг). Построим на отрезке  сетку
сетку  .
.
Пусть  – точное решение задачи в точке
– точное решение задачи в точке  , а
, а  – приближенное в этой же точке. Запишем разложение функции
– приближенное в этой же точке. Запишем разложение функции  в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки  :
:
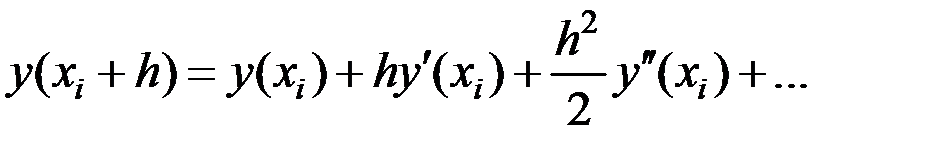 (6.12)
(6.12)
Используя линейную часть разложения и заменив  на
на 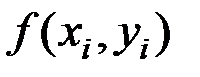 , получим известную формулу метода Эйлера:
, получим известную формулу метода Эйлера:
 (6.13)
(6.13)
Формула позволяет найти приближенное решение в точке  через значение решения в точке
через значение решения в точке  . Это решение согласуется с разложением в ряд Тейлора вплоть до членов порядка
. Это решение согласуется с разложением в ряд Тейлора вплоть до членов порядка 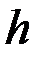 , то есть ошибка ограничения метода на одном шаге равна
, то есть ошибка ограничения метода на одном шаге равна  ,
, 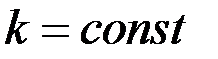 или
или  . Очевидно, что полученная формула (6.13) есть уравнение касательной в точке
. Очевидно, что полученная формула (6.13) есть уравнение касательной в точке 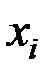 к графику точного решения, проведенной с тангенсом угла наклона, равным
к графику точного решения, проведенной с тангенсом угла наклона, равным  .
.
Метод Эйлера – самый грубый из серии методов Рунге-Кутта. Он называется методом Рунге-Кутта первого порядка, так как согласуется с разложением в ряд Тейлора вплоть до членов порядка 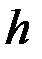 . Вычисления начинаются с точки
. Вычисления начинаются с точки 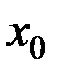 , где
, где  . Ошибка, полученная на первом шаге, далее увеличивается с ростом
. Ошибка, полученная на первом шаге, далее увеличивается с ростом  .
.
Если в формуле (6.12) заменить вторую производную соотношением

тогда
 (6.14)
(6.14)
Приближенная формула в этом случае имеет вид:
|
|
|
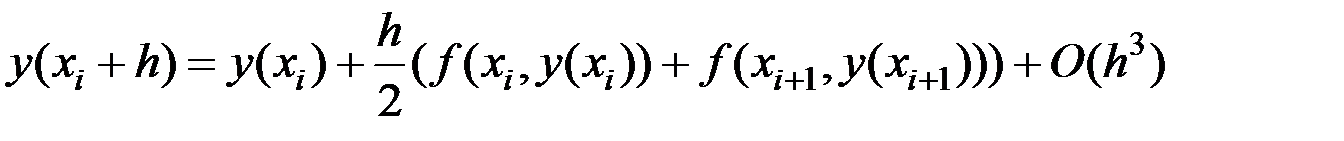 (6.15)
(6.15)
Эта формула неявного метода, так как неизвестное значение присутствует как в левой, так и в правой части в виде аргумента функции  .
.
Ввиду произвольности функции  использование формулы (6.15) может привести к тому, что для отыскания значения
использование формулы (6.15) может привести к тому, что для отыскания значения  на каждом шаге придется решать нелинейное уравнение. Заменим
на каждом шаге придется решать нелинейное уравнение. Заменим  на
на  в правой части формулы (6.15) с погрешностью, пропорциональной
в правой части формулы (6.15) с погрешностью, пропорциональной 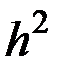 , то есть
, то есть 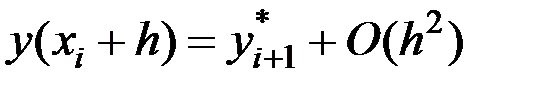 , где в качестве
, где в качестве  можно взять значение, вычисленное по методу Эйлера:
можно взять значение, вычисленное по методу Эйлера:  .
.
Тогда правая часть формулы (6.15) изменится на величину
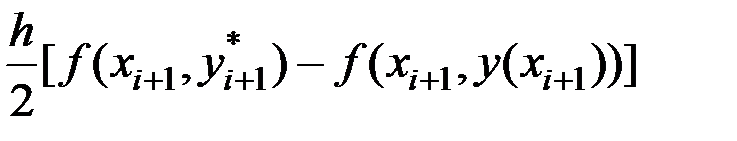
 ,
,
где  , то есть разность имеет погрешность, пропорциональную
, то есть разность имеет погрешность, пропорциональную  .
.
Таким образом, вместо формулы (6.15) получим схему явного метода Рунге-Кутта второго порядка:
 . (6.16)
. (6.16)
Аналогично можно получить другую формулу метода второго порядка с ошибкой на шаге, пропорциональной  , то есть
, то есть
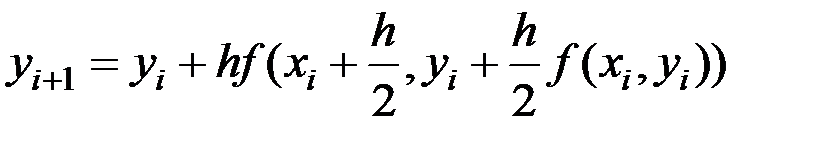 (6.17)
(6.17)
Метод Рунге-Кутта (6.17) согласуется с разложением в ряд Тейлора вплоть до членов порядка  .
.
Наиболее распространенным из этой группы методов является метод Рунге-Кутта четвертого порядка, для которого ошибка ограничения на одном шаге  . Определение приближенного решения на основе данного метода осуществляется по следующим формулам:
. Определение приближенного решения на основе данного метода осуществляется по следующим формулам:
|
|
|
 (6.18)
(6.18)
где 

Справедливость приведенных формул проиллюстрируем на следующей элементарной задаче:
 (6.19)
(6.19)
Точное решение имеет вид:  , где
, где 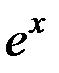 можно представить в окрестности точки
можно представить в окрестности точки  в виде суммы ряда Тейлора:
в виде суммы ряда Тейлора:  Воспользуемся приближенным методом (6.16) для решения данной задачи. В данном случае
Воспользуемся приближенным методом (6.16) для решения данной задачи. В данном случае 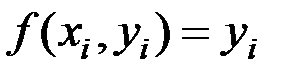 , в результате получим:
, в результате получим:
 .
.
Подставим это выражение в формулу (6.16):
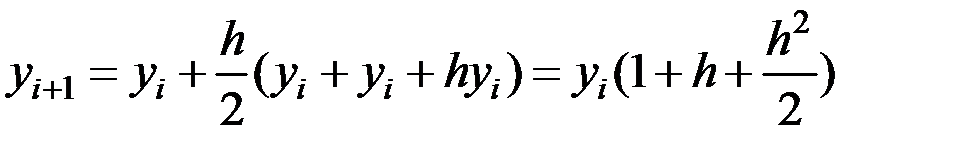
или
 .
.
Отсюда  .
.
Т.е.  , т.к.
, т.к.  , чего и следовало ожидать.
, чего и следовало ожидать.
Если для задачи (6.19) применить приближенные формулы (6.18), то получим:

 .
.


 или
или  .
.
Однако в этом случае приближенное решение совпадает с первыми пятью членами разложения точного решения в ряд Тейлора.
Рассматриваемые методы относятся к семейству методов Рунге-Кутта и называются одношаговыми, так как позволяют получить приближения  к точному решению
к точному решению 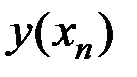 в каждом узле сетки
в каждом узле сетки  на основе известного приближения
на основе известного приближения 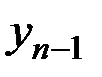 к решению в предыдущем узле
к решению в предыдущем узле 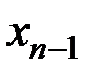 . При этом погрешность метода на каждом шаге равна
. При этом погрешность метода на каждом шаге равна  , где
, где  – порядок метода. Однако практически определить величину
– порядок метода. Однако практически определить величину  трудно и, соответственно, трудно выбрать величину шага
трудно и, соответственно, трудно выбрать величину шага 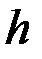 для вычислений. Для этого используют различные практические способы оценки. Например, правило Рунге оценки погрешности заключается в том, что по одной и той же формуле метода определенного порядка вычисляются приближения к решению в одной точке, но с разными шагами, которые затем используются для получения апостериорной оценки погрешности.
для вычислений. Для этого используют различные практические способы оценки. Например, правило Рунге оценки погрешности заключается в том, что по одной и той же формуле метода определенного порядка вычисляются приближения к решению в одной точке, но с разными шагами, которые затем используются для получения апостериорной оценки погрешности.
|
|
|
Пусть в начальном узле  известно решение
известно решение 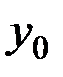 . Значение, вычисленное в точке
. Значение, вычисленное в точке 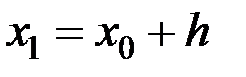 с шагом
с шагом  , обозначим
, обозначим  . Значение, полученное в точке
. Значение, полученное в точке  через два последовательных шага
через два последовательных шага  из точки
из точки  , обозначим
, обозначим  . Можно показать, что справедлива оценка:
. Можно показать, что справедлива оценка:
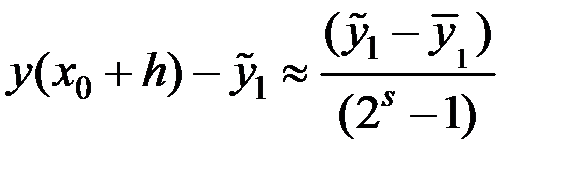 , (6.20)
, (6.20)
где  – точное решение в точке
– точное решение в точке 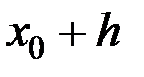 .
.
Дата добавления: 2022-07-01; просмотров: 22; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
