Использование свойств возрастающих и убывающих функций.
Иррациональные уравнения.
Иррациональными уравнениями называются уравнения, содержащие переменную под знаком радикала (корня) или под знаком возведения в дробную степень. При этом, степень корня может быть произвольной.
Например, 
Из определения следует, что если в записи уравнения нет знака корня (или дробного показателя степени), то уравнение не является иррациональным. Однако, не все уравнения, содержащие знаки корней, являются иррациональными. Действительно, в иррациональном уравнении под знаком корня должна быть переменная, и если её там нет, то уравнение не является иррациональным.
Например,  В этих уравнениях под знаком корня стоят числа, а не переменные, значит, они не являются иррациональными.
В этих уравнениях под знаком корня стоят числа, а не переменные, значит, они не являются иррациональными.
Перечислим основные методы решения иррациональных уравнений.
По определению корня.
Метод возведения обеих частей уравнения в одну и ту же степень.
Метод введения новой переменной.
Метод разложения на множители.
Функционально-графический метод.
Решение иррациональных уравнений через ОДЗ.
Решение иррациональных уравнений вида «дробь равна нулю».
Приведение иррациональных уравнений к числовым равенствам.
Переход к модулям.
Преобразование иррациональных уравнений.
Рассмотрим каждый из перечисленных методов.
1) С помощью определения корня обычно решаются простейшие иррациональные уравнения, т.е. уравнения вида  , где
, где  и
и  – некоторые рациональные выражения. Решение таких уравнений зависит от чётности показателя корня.
– некоторые рациональные выражения. Решение таких уравнений зависит от чётности показателя корня.
|
|
|
Рассмотрим сначала случай, когда в правой части содержится число, т.е.
 .
.
· Если п – чётное, т.е.  , где
, где  , то
, то

· Если п – нечётное, т.е.  , где
, где  , то
, то

Теперь рассмотрим случай, когда в правой части стоит выражение, зависящее от х, т.е.

· Если п – чётное, т.е.  , где
, где  , то
, то

· Если п – нечётное, т.е.  , где
, где  , то
, то

Например,
а) 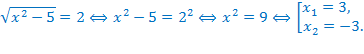
б) 
в) 
г) 

д) 

2) В основе метода возведения обеих частей уравнения в одну и ту же степень лежит следующее утверждение:
Возведение обеих частей уравнения в одну и ту же чётную натуральную степень даёт уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечётную степень даёт равносильное уравнение.
Поэтому, при возведении в чётную степень, необходимо находить область допустимых значений, либо выполнять проверку для найденных корней.
Этот метод обычно используется при решении уравнений вида 
· Если п – чётное, т.е.  , где
, где  , то
, то

|
|
|
Для упрощения записи решения уравнения, неравенства можно вынести в ОДЗ. Это будет выглядеть так:
 ОДЗ:
ОДЗ: 

· Если п – нечётное, т.е.  , где
, где  , то
, то

Например,
а)  ОДЗ:
ОДЗ: 






 ОДЗ, значит, этот корень посторонний.
ОДЗ, значит, этот корень посторонний.
Ответ: 5,5
б) 


Ответ: 1
в)  ОДЗ:
ОДЗ: 

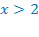




Оба корня принадлежат области допустимых значений, значит, они являются корнями исходного уравнения.
Ответ: 6; 18.
г)  ОДЗ:
ОДЗ: 






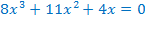

 или
или 
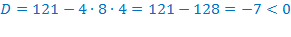 , значит,
, значит,
уравнение не имеет действительных корней.
|
|
|
 принадлежит области допустимых значений, значит, этот корень является корнем исходного уравнения.
принадлежит области допустимых значений, значит, этот корень является корнем исходного уравнения.
Ответ: 0.
д)  ОДЗ:
ОДЗ: 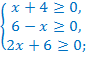
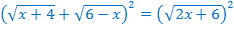






Теперь к области допустимых значений добавляется ещё одно условие: 
 ОДЗ:
ОДЗ: 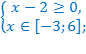

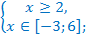




 не принадлежат области допустимых значений, значит, этот корень посторонний.
не принадлежат области допустимых значений, значит, этот корень посторонний.
Ответ: 5.
3) Удобным методом решения иррациональных уравнений является метод введения новой переменной. Метод, обычно, применяется в случае, если в уравнении неоднократно встречается некоторое выражение с переменной. Тогда имеет смысл обозначить это выражение другой переменной.
Более сложным является случай, когда в уравнении присутствуют корни разных степеней. В этом случае есть смысл обозначить каждый корень другой переменной. Это можно выразить формулой:
|
|
|

Например,
а) 
Так как в уравнении присутствует корень нечётной степени, то находить ОДЗ не имеет смысла.
Введём новую переменную:  , тогда
, тогда  . Значит, исходное уравнение принимает вид:
. Значит, исходное уравнение принимает вид:


Возвращаемся к исходной переменной:


Ответ: 
б)  ОДЗ:
ОДЗ: 
Введём новые переменные: 
 .
.
Тогда исходное уравнение равносильно системе:

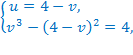

Решим кубическое уравнение методом разложения на множители:



 или
или 

 корней нет.
корней нет.

Возвращаемся к исходной переменной. Для этого достаточно использовать только одну из двух замен.



Ответ: 1.
4) Метод разложения на множители используется тогда, когда достаточно просто найти общие множители в записи уравнения. Общий множитель выносится за скобки и используется свойство равенства нулю произведения.

Например, а) 
ОДЗ: 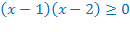

Вынесем за скобки 

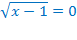 или
или 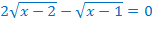




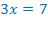

Оба корня принадлежат области допустимых значений.
Ответ: 
б) 


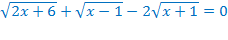 или
или 




ОДЗ: 



 или
или 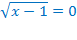





Ответ: 
5) Функционально-графический метод используется в тех иррациональных уравнениях, когда остальные методы бессильны.
Можно выделить три основных направления функционально-графического метода решения иррациональных уравнений:
· использование графиков функций (графический метод);
· использование свойств возрастающих и убывающих функций (использование монотонности функций);
· использование свойств ограниченных функций (метод оценки).
Эти три направления помогают решить подавляющее большинство иррациональных уравнений.
Графический метод.
Обычно, этим методом решаются те уравнения, которые невозможно решить другим методом и графики функций, входящих в состав уравнения являются элементарными или получаются из таковых геометрическим преобразованием (растяжение, сжатие, смещение, сложение и вычитание).
Алгоритм использования графического метода:
˗ построить графики функций, входящих в уравнение;
˗ по взаимному расположению графиков сделать вывод о наличии и количестве корней решаемого уравнения:
а) если графики функций не пересекаются, то уравнение корней не имеет;
б) если графики функций имеют общие точки, то корнями уравнения являются абсциссы этих точек.
Следует учитывать, что, используя графический метод, сложно достичь высокой точности нахождения корней, поэтому, все найденные корни уравнения будут лишь приближёнными, нуждающимися в проверке и обосновании.
Для наглядности приведём простой пример.

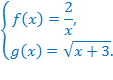
На одной системе координат строим графики функций  и
и  .
.
Графики этих функций пересекаются в одной точке, значит, уравнение имеет один корень. Точка пересечения имеет координаты  , значит,
, значит,  . Произведя проверку, убеждаемся, что этот корень точный.
. Произведя проверку, убеждаемся, что этот корень точный.


Равенство верное, значит,  .
.
Ответ: 1.
Использование свойств возрастающих и убывающих функций.
Часто вместо графиков удобнее использовать свойства монотонности функций (свойства возрастания и убывания). Это происходит чаще всего в тех случаях, когда нужно найти количество корней уравнения.
Этот метод основывается на утверждении, которое следует из определения возрастания и убывания функции.
Если на множестве Х функции  и
и  непрерывны и одна из них возрастает, а другая убывает, то уравнение
непрерывны и одна из них возрастает, а другая убывает, то уравнение  либо имеет единственный корень, либо не имеет корней.
либо имеет единственный корень, либо не имеет корней.
Это утверждение верно как для иррациональных уравнений, так и для любых других.
Что касается нахождения значения корня уравнения, то, обычно, он является числом из ОДЗ и легко угадывается. Проверкой определяется правильность выбора корня.
Приведём пример.  .
.
Найдём область допустимых значений уравнения:
ОДЗ: 
Функции  и
и  непрерывны на всей области допустимых значений.
непрерывны на всей области допустимых значений.
Исследуем на монотонность функции  и
и  для
для  .
.
а) Функция  – линейная, угловой коэффициент у неё отрицательный, значит, она убывающая на всей области определения. Корень из убывающей функции – есть функция убывающая, значит,
– линейная, угловой коэффициент у неё отрицательный, значит, она убывающая на всей области определения. Корень из убывающей функции – есть функция убывающая, значит,  – убывающая для
– убывающая для  . Функция
. Функция  – обратная пропорциональность, она убывающая для всех
– обратная пропорциональность, она убывающая для всех  , т.к. коэффициент
, т.к. коэффициент  . Значит, функция
. Значит, функция  , равная сумме убывающих функций является убывающей на отрезке
, равная сумме убывающих функций является убывающей на отрезке  .
.
б) Функция  – кубическая, она возрастающая на всей области определения, т.к. коэффициент положительный; функция
– кубическая, она возрастающая на всей области определения, т.к. коэффициент положительный; функция  также возрастающая при
также возрастающая при  .
.
Итак, при  функции, записанные в левой и правой частях уравнения являются непрерывными, причём одна из них убывает, а другая возрастает. Значит, уравнение либо не имеет корней, либо имеет единственный корень. Попробуем его отыскать. Методом подбора предполагаем, что
функции, записанные в левой и правой частях уравнения являются непрерывными, причём одна из них убывает, а другая возрастает. Значит, уравнение либо не имеет корней, либо имеет единственный корень. Попробуем его отыскать. Методом подбора предполагаем, что  и выполним проверку:
и выполним проверку: 



Равенство получилось верное, значит, уравнение имеет единственный корень  .
.
Ответ: 0.
Метод оценки.
Этот метод использует ограниченность функций.
Алгоритм метода оценки.
˗ оцениваем значения функций в обеих частях уравнения;
˗ ищем корни уравнения, используя полученные оценки, или обосновываем их отсутствие.
Способов оценки значений функции существует несколько. Мы рассмотрим все способы, поскольку в иррациональных уравнениях могут использоваться не только выражения с корнем.
а) оценка на основании определения корня с чётным показателем;
б) оценка на основании свойства корней: если  , то
, то  ;
;
в) оценка на основании свойства степени с чётным показателем: 
г) оценка значений квадратного трёхчлена;
д) оценка на основании свойств числовых неравенств;
е) оценка с использованием наибольшего и наименьшего значений функции.
Рассмотрим их подробнее.
а) Т.к., по определению, корень с чётным показателем есть неотрицательное число, то для любого х из области допустимых значений справедливо неравенство  , где
, где  – некоторое выражение. Причём, понятно, что
– некоторое выражение. Причём, понятно, что  только тогда, когда
только тогда, когда  .
.
б) Если выполняется неравенство  , где
, где  , то для любого х из области допустимых значений справедливо неравенство
, то для любого х из области допустимых значений справедливо неравенство  .
.
в) Так как любое число в чётной степени есть неотрицательное число, то это свойство распространяется и на многочлены, т.е. для любого х из области допустимых значений справедливо неравенство  . Также понятно, что
. Также понятно, что  тогда и только тогда, когда
тогда и только тогда, когда  .
.
г) Если выражение задано в виде квадратного трёхчлена, то для его оценки необходимо сначала проверить на знак дискриминант.
· Если  , то значение квадратного трёхчлена оцениваем с помощью ординаты вершины параболы. Напомним, что
, то значение квадратного трёхчлена оцениваем с помощью ординаты вершины параболы. Напомним, что  . Тогда
. Тогда  , если
, если  (ветви параболы направлены вверх); и
(ветви параболы направлены вверх); и  , если
, если  (ветви параболы направлены вниз).
(ветви параболы направлены вниз).
· Если  , то значение квадратного трёхчлена сравниваем с нулём: если
, то значение квадратного трёхчлена сравниваем с нулём: если  , то
, то  , если
, если  , то
, то  .
.
д) Оценка на основе свойств числовых неравенств. Вспомним эти свойства.
· Если к обеим частям верного неравенства прибавить (или отнять) некоторое число, то получится равносильное неравенство.
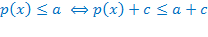 , где a и с – некоторые числа.
, где a и с – некоторые числа.
· Если обе части верного неравенства умножить (или разделить) на одно и то же положительное число, то получится равносильное неравенство.
 , где а и с – некоторые числа, причём
, где а и с – некоторые числа, причём  .
.
· Если обе части верного неравенства умножить (или разделить) на одно и то же отрицательное число и поменять знак неравенства на противоположный, то получится равносильное неравенство.
 , где а и с – некоторые числа, причём
, где а и с – некоторые числа, причём  .
.
· Если в верном неравенстве обе положительные части заменить обратными выражениями и поменять знак неравенства на противоположный, то получится равносильное неравенство на всей области допустимых значений.
 , где
, где  .
.
· Если верные неравенства почленно сложить, то получится верное неравенство.
Если  , где
, где  - некоторые числа, то справедливо неравенство:
- некоторые числа, то справедливо неравенство:
 .
.
· Если верные неравенства с положительными левой и правой частями почленно умножить, то получится верное неравенство.
Если  , где
, где  – положительные выражения, и
– положительные выражения, и  - положительные числа, то справедливы неравенства:
- положительные числа, то справедливы неравенства:
 .
.
· Если  , причём
, причём  , то
, то  .
.
е) Оценка с использованием наибольшего и наименьшего значения функции.
· Если наименьшее значение функции  равно
равно  , то
, то  , на всей области определения.
, на всей области определения.
· Если наибольшее значение функции  равно
равно  , то
, то  , на всей области определения.
, на всей области определения.
После оценки значений функции, нужно сделать заключение о существовании решений уравнения.
1) Уравнение  не имеет решений на множестве допустимых значений, если:
не имеет решений на множестве допустимых значений, если:
Ø 
Ø 
Ø 
Ø 
Ø 
Ø 
2) Уравнение  равносильно системе уравнений
равносильно системе уравнений  на множестве допустимых значений, если:
на множестве допустимых значений, если:
Ø  , где
, где  и
и 
Ø  , где
, где  и
и 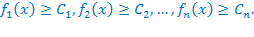
Ø  , где
, где  и
и 
Ø  , где
, где  и
и  , причём
, причём  – неотрицательные числа.
– неотрицательные числа.
3) Уравнение  не имеет решений на множестве допустимых значений, если:
не имеет решений на множестве допустимых значений, если:
Ø 
Ø 
Ø 
Ø 
Ø 
Ø 
Ø 
4) Уравнение  равносильно системе уравнений
равносильно системе уравнений  для любого х из области допустимых значений, если
для любого х из области допустимых значений, если  (или наоборот).
(или наоборот).
Приведём примеры.
а) 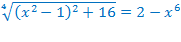
Произведём оценку левой и правой части уравнения.
Обозначим  ,
,  .
.
˗ Т.к.  при любом значении х, то
при любом значении х, то  при любом х, а это значит, что
при любом х, а это значит, что 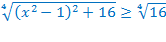 . Поэтому,
. Поэтому, 
˗ Т.к.  , то
, то  , а значит,
, а значит,  . Поэтому,
. Поэтому,  .
.
Мы получили, что  , а
, а  . Значит, исходное уравнение равносильно системе двух уравнений:
. Значит, исходное уравнение равносильно системе двух уравнений:

Из второго уравнения легко найден единственный корень  . Подставив его в первое уравнение, мы получили неверное равенство. Это означает, что система уравнений, а, значит, и исходное уравнение решений не имеет.
. Подставив его в первое уравнение, мы получили неверное равенство. Это означает, что система уравнений, а, значит, и исходное уравнение решений не имеет.
Ответ: решений нет.
б) 
Зададим функцию  . Она состоит из суммы трёх слагаемых, значит,
. Она состоит из суммы трёх слагаемых, значит,  , где
, где  . Произведём оценку каждой из этих функций.
. Произведём оценку каждой из этих функций.
˗ Т.к.  , то
, то  , значит,
, значит,  . Поэтому,
. Поэтому, 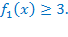
˗ Т.к.  , то
, то  , значит,
, значит,  . Поэтому,
. Поэтому, 
˗ Т.к.  , то
, то  , значит,
, значит, 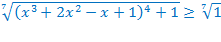 . Поэтому,
. Поэтому, 
Зная, что  ,
,  ,
,  и
и  , заключаем, что
, заключаем, что 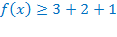 , т.е.
, т.е. 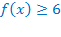 . А т.к.
. А т.к.  , то исходное уравнение решений не имеет.
, то исходное уравнение решений не имеет.
Ответ: решений нет.
в) Рассмотрим похожий пример:  .
.
Рассуждения такие же, как и в предыдущем примере.
 .
.
˗ Т.к.  , то
, то  , значит,
, значит,  . Поэтому,
. Поэтому, 
˗ Т.к.  , то
, то  , значит,
, значит,  . Поэтому,
. Поэтому, 
Значит,  . Используя пункт 2 из метода оценки, переходим к системе:
. Используя пункт 2 из метода оценки, переходим к системе:


Ответ: 2.
6) Метод использования области допустимых значений (ОДЗ) является частью решения иррациональных уравнений, поскольку, практически всегда в таких уравнениях находим ОДЗ.
· Если областью допустимых значений уравнения является пустое множество, значит, уравнение корней не имеет.
· Если область допустимых значений имеет конечное множество чисел, то, подставляя каждое из них в исходное уравнение, находим корни.
· Если область допустимых значений имеет бесконечное множество чисел, то рассматриваем другой способ решения.
Приведём примеры.
а) 
Найдём область допустимых значений.
 .
.
Область допустимых значений состоит из пустого множества, значит, исходное уравнение корней не имеет.
Ответ: корней нет.
б) 
Найдём область допустимых значений.

Так как область допустимых значений состоит из двух чисел  и
и  , то проверим, обращает ли каждое из них исходное уравнение в верное равенство.
, то проверим, обращает ли каждое из них исходное уравнение в верное равенство.


Значит,  является корнем уравнения.
является корнем уравнения.
в) 
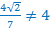
Значит,  не является корнем уравнения.
не является корнем уравнения.
Ответ:  .
.
Дата добавления: 2022-06-11; просмотров: 42; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
