Интервальный ряд распределения фирм по среднесписочной численности менеджеров в одном из регионов РФ в I квартале отчетного года

Понятие и расчет структурных средних

Структурные средние (непараметрические средние) характеризуют величину варианта, занимающего определенное положение в ранжированном ряду.

Наиболее известные из них — мода и медиана.

Мода (Мо) — наиболее часто встречающееся значение признака.

Медиана (Me) — значение признака, приходящееся на середину ранжированного ряда.

Для дискретного ряда распределения мода и медиана находятся довольно легко с помощью таблицы.

Моде соответствует максимальная частота.

Медианой следует считать значение признака в той группе, в которой накопленная частота впервые превысит половину численности совокупности.

Для интервального ряда распределения с целью определения моды и медианы сначала находят модальный и медианный интервалы — по тем же правилам, по которым находят моду и медиану для дискретного ряда распределения. Затем в модальном и медианном интервалах определяют точечные значения моды и медианы — см. далее формулы (4.46) и (4.54).

Мода для интервального ряда распределения с равными интервалами определяется по формуле

где х ₀ — нижняя граница модального интервала; х _{ — верхняя граница модального интервала;/_Мо — частота модального интервала; /_Мо_1 — частота интервала, предшествующего модальному;/_Мо+1 — частота интервала, следующего за модальным.

Приведем вывод формулы расчета моды для интервального ряда распределения (4.46).

Для пояснения этого вывода предложим к рассмотрению фрагмент условной гистограммы распределения единиц совокупности.

На гистограмме мы продолжили вверх линию, соответствующую нижней границе модального интервала (х₀). На этой линии отложили отрезок, равный (f _Mo -/_Мо_!). Соединили отрезком полученную точку А с левым верхним углом следующего за модальным столбика (точка В).

Собственно, точка пересечения построенного отрезка с вершиной модального столбика (точка С) и есть искомое точечное значение моды.

Дальше выводим расчетную формулу определения точечного значения моды для интервального ряда. Исходим из следующего.

Если некая функция имеет максимум в некоторой точке (у нас это точка С), то вблизи этой точки производная слева долж-

Рис. 4.1. Фрагмент условной гистограммы распределения для пояснения выводов показателя моды для интервального ряда распределения

на равняться минус производной справа. Помним, что производная — это тангенс угла наклона касательной к исследуемой кривой (в нашем случае это угол а). В точках, соответствующих максимуму функции, производная будет равна нулю.

(dy ДдЛ

Переходя от производных к конечным результатам — ~ — .

V dx х )

для нашего случая можно написать ⁴ '

где h = х, - х₀ — длина интервала; х' — отрезок, длина которого равна расстоянию от начала модального интервала (х₀) до точечного значения моды.

Используя полученное равенство, определим лЛ Для этого делаем несложные преобразования.

Отсюда

Тогда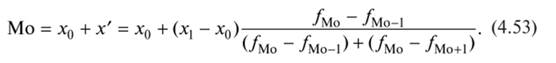

Сквозная задача Задание 4.2

На основании данных интервального ряда распределения фирм по среднесписочной численности менеджеров (табл. 4.2) требуется рассчитать моду и сделать вывод.

Таблица 4.2

Интервальный ряд распределения фирм по среднесписочной численности менеджеров в одном из регионов РФ в I квартале отчетного года

Численность менеджеров, чел., ^X J	Число фирм, ед., ft
15-20	3
20-25	6
25-30	8
30-35	7
35-40	5
40-45	1
ИТОГО	30

Решение:

Модальный интервал 25—30, так как частота его максимальная (/'з = 8). Определяем для модального интервала точечное значение моды:

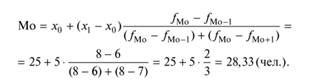
Вывод. Чаще всего встречаются фирмы со среднесписочной

численностью менеджеров 28,33 человека.

Медиана для интервального ряда распределения с равными интервалами определяется по следующей формуле:

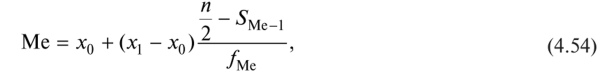
где х₀ — нижняя граница медианного интервала; х _{ — верхняя граница медианного интервала; — накопленная частота интервала, предшествующего медианному; /_Ме — частота медианного интервала.

Приведем вывод формулы расчета медианы для интервального ряда распределения (4.20). Сделаем это также с помощью некой условной гистограммы распределения единиц совокупности.

По определению медианы площадь многоугольника ОЛСМе равна

Рис. 4.2. Условная гистограмма распределения для пояснения выводов показателя медианы для интервального ряда распределения

Площадь ОАВх _п равна

Таким образом, площадь прямоугольника x₀Z)CMe — это разность площадей ОАСМе и ОАВх ₀ .

Следовательно, длина отрезка л^Ме равна

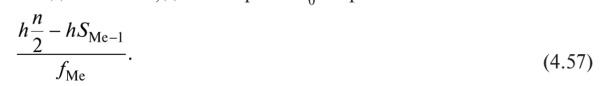
Отсюда получаем искомое выражение (4.54):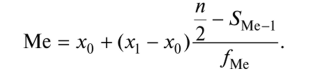

Сквозная задача

Задание 4.3

На основании данных интервального ряда распределения фирм по среднесписочной численности менеджеров (табл. 4.2) требуется рассчитать медиану и сделать вывод.

Решение:

На базе исходной табл. 4.2 построим вспомогательную табл. 4.3.

Таблица 4.3

Вспомогательная таблица для расчета медианы

Численность менеджеров, чел., ^x j	Число фирм, ед., fj	Накопленное число фирм к Ifj j=¹
15-20	3	3 < 15
20-25	6	9< 15
25-30	8	17 > 15
30-35	7
35-40	5
40-45	1
ИТОГО	30

Теперь определяем медианный интервал.

Медианный интервал 25—30, так как накопленная частота (накопленное число фирм) именно в этом интервале впервые превысила величину, равную половине объема ряда распределения (— = — = 15), т.е. половине числа всех фирм.

Определяем для медианного интервала ряда распределения точечное значение медианы:

Вывод. Половина фирм имеет среднесписочную численность менеджеров не более 28,75 человека, другая половина — не менее 28,75 человека.

С целью более подробного изучения структуры вариационного ряда рассчитывают также квартили, децили и перцентили, расчет которых подобен расчету медианы.

Квартили (Q) — структурные характеристики, делящие ранжированный ряд на 4 части, равные по числу единиц:

Сквозная задача

Задание 4.4

На основании данных интервального ряда распределения фирм по среднесписочной численности менеджеров (табл. 4.2) требуется рассчитать квартили и сделать вывод.

Решение:

На базе исходной табл. 4.2 построим вспомогательную табл. 4.4.

Вспомогательная таблица для расчета квартилей

Численность менеджеров, чел., ^x j	Число фирм, ед., fj	Накопленное число фирм к I f, м
15-20	3	3
20-25	6	9 >7,5
25-30	8	17
30-35	7	24 >22,5
35-40	5	29
40-45	1	30
ИТОГО	30

Определяем Or. тогда

Вывод. Первая четверть фирм исследуемого ряда распределения имеет среднесписочную численность менеджеров не более 23,75 человека, другие три четверти — не менее 23,75 человека.

Q ₂ = Me = 29 чел. (см. задание 4.3).

Определяем Q ₃ :

тогда

Вывод. Первые три четверти фирм исследуемого ряда распределения имеют среднесписочную численность менеджеров не более 33,93 человека, оставшаяся четверть — не менее 33,93 человека.

Децили — это значения признаков, которые делят ранжированный ряд на десять равных частей.

Перцентили — это значения признаков, которые делят ранжированный ряд на сто равных частей.

Дата добавления: 2022-06-11; просмотров: 75; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!