Числовые и функциональные ряды

Дифференциальные уравнения

Дифференциальные уравнения первого порядка

I . Дифференциальные уравнения с разделяющимися переменными

Уравнение вида

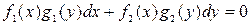(1)

называется дифференциальным уравнением с разделяющимися переменными. Оно решается путем почленного деления его на .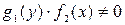

Получаем: 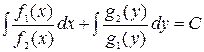– общий интеграл данного дифференциального уравнения.

Пример 1. Найти общий интеграл дифференциального уравнения

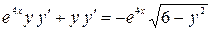Решение: Приведем данное уравнение к виду (1)

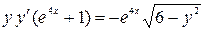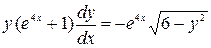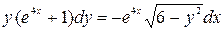Разделим обе части уравнения на :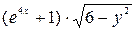

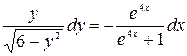Интегрируем обе части уравнения

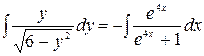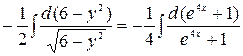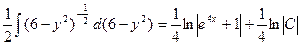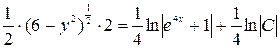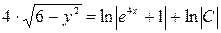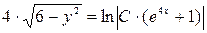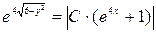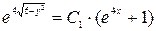− общий интеграл дифференциального уравнения.

Ответ: .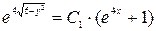

II . Однородные дифференциальные уравнения

Функция 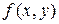называется однородной функцией п-го порядка, если выполняется равенство .

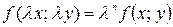Дифференциальное уравнение вида

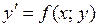(2)

называется однородным, если функция 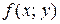является однородной нулевого порядка.

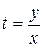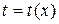Уравнение (2) решается путем введения замены , где – некоторая функция, тогда .

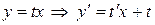Пример 2. Решить уравнение

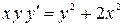Решение: Приведем уравнение к виду (2)

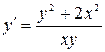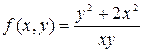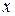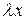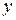В данном случае . Заменим на , − на 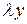, получим

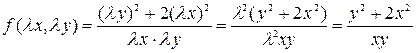Так как функция не изменилась, то 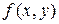является однородной функцией нулевого порядка. Следовательно, данное дифференциальное уравнение является однородным.

Введем замену 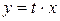, тогда .

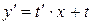Уравнение примет вид

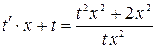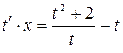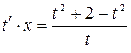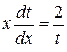Разделим обе части уравнения на 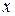и умножим на 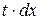, получим

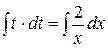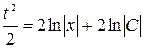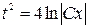Возвращаемся к исходной переменной: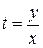

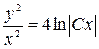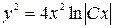Ответ: .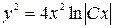

III . Линейные дифференциальные уравнения

Уравнение вида

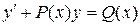(3)

называется линейным.

Если 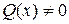, то уравнение называется линейным неоднородным (ЛНДУ), а если 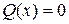, то линейным однородным (ЛОДУ).

Решение ЛНДУ можно найти двумя способами.

1) Метод Бернулли

Решение уравнения (2) ищут в виде произведения двух функций, зависящих от переменной х: 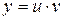, причем одну из них можно выбрать произвольно, например, .

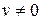Дифференцируя 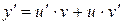, подставляют у и 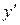в данное уравнение

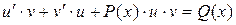или

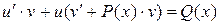. (4)

Выбираем функцию v такой, чтобы множитель в скобках был равен нулю, т.е.

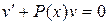или ,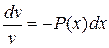

Получили уравнение с разделяющимися переменными, его решением является функция .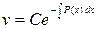

Ввиду свободы выбора v, положим 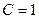, тогда .

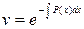Уравнение (4) запишем в виде: .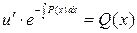

Разделяя переменные, найдем общий интеграл этого уравнения

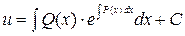Возвращаясь к переменной у, получим общее решение:

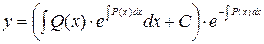2) Метод Лагранжа или метод вариации произвольной постоянной

Сначала находим общее решение ЛОДУ 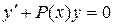. Оно является уравнением с разделяющимися переменными, то есть,

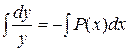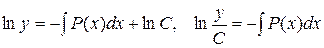или 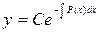, где .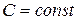

Исходя из общего решения соответствующего ЛОДУ данного уравнения 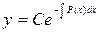, варьируют произвольную постоянную, т.е. С заменяют дифференцируемой функцией С(х). Для отыскания С(х) находят 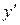и подставляют у и 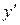в данное уравнение.

Пример 3. Решить уравнение

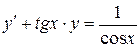Решение: Так как искомая функция 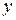и ее производная 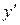входят в данное уравнение в первой степени, то это уравнение является линейным.

Ищем решение уравнения в виде 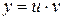, тогда .

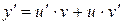Уравнение примет вид

(*)

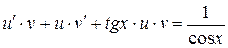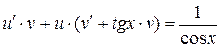Подберем функцию 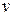такой, чтобы выражение, стоящее в скобках было равно нулю 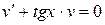или .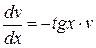

Разделим обе части уравнения на 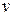и умножим на 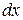, получим

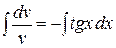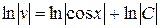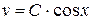
Нам достаточно иметь какое-нибудь одно ненулевое решение, положим 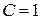, тогда .

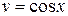Подставим 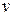в уравнение (*):

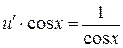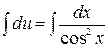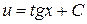Окончательно получим ,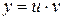

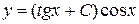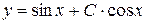Ответ: .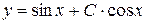

Дифференциальные уравнения второго порядка

IV . Дифференциальные уравнения вида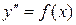

Для решения такого уравнения следует проинтегрировать два раза его правую часть:

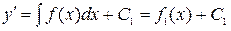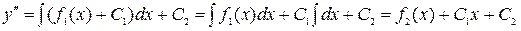Пример 4. Найти частное решение уравнения, удовлетворяющее заданным начальным условиям

, ,

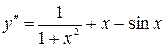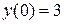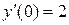
Решение:

1. Находим общее решение, интегрируя два раза правую часть

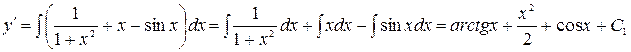
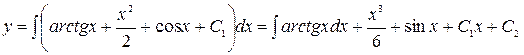
Для вычисления 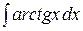применим метод интегрирования по частям:

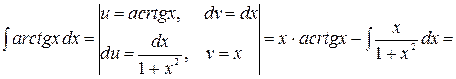
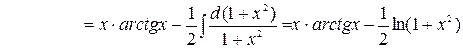Получим общее решение .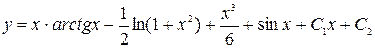

2. Находим частное решение, используя начальные условия

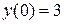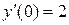
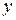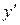В выражения для и подставим 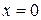, , 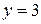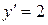. Получим систему относительно 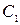и :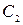

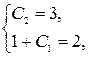
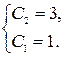
Найденные значения постоянных подставляем в общее решение, получаем искомое частное решение

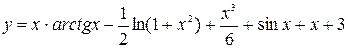Ответ: .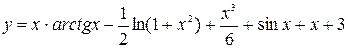

VII . Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейным однородным дифференциальным уравнением (ЛОДУ) второго порядка с постоянными коэффициентами называется уравнение вида:

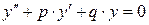где p, q – некоторые действительные числа.

Для решения данного уравнения составляют характеристическое уравнение

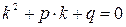При решении характеристического уравнения возможны три случая:

1) корни действительные различные .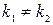

Общее решение ЛОДУ имеет вид:

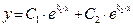2) корень действительный двукратный .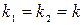

Общее решение ЛОДУ имеет вид:

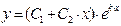3) корни комплексные сопряженные .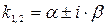

Общее решение ЛОДУ имеет вид:

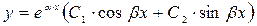VIII . Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейным неоднородным дифференциальным уравнением (ЛНДУ) 2-го порядка с постоянными коэффициентами называется уравнение вида:

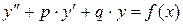
Общее решение ЛНДУ равно сумме любого его частного решения и общего решения, соответствующего ЛОДУ, т.е. ,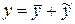

где 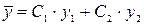- общее решение соответствующего ЛОДУ,

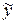- частное решение ЛНДУ.

Частное решение ЛНДУ может быть найдено с помощью метода неопределенных коэффициентов.

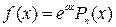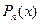1. Пусть , где - многочлен n-й степени.

а) Число а не является корнем характеристического уравнения.

Тогда частное решение ищем в виде ,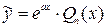

где 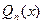- общий вид многочлена n-й степени.

б) Число а является корнем характеристического уравнения кратности 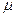, тогда .

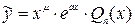Есл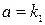и и 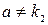, то есть, характеристическое уравнение имеет различные корни и число 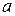совпадает с одним из них, тогда .

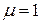Если 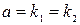, тогда .

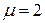Примечание.

Если 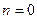, то .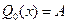

Если 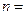1, то .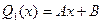

Если 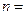2, то .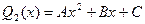

Если 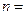3, то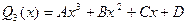

2. Пусть ,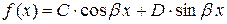

где 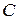, 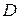– некоторые числа.

а) Число 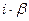не является корнем характеристического уравнения, тогда

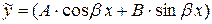где 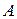и 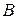– неопределенные коэффициенты.

б) Число 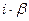является корнем характеристического уравнения кратности 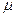, тогда .

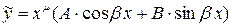3. Пусть ,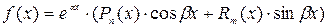

где 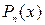- многочлен n-й степени,

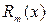- многочлен m-й степени.

а) Число 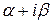не является корнем характеристического уравнения.

Тогда ,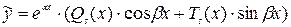

где 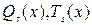- общий вид многочленов s-й степени, .

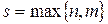б) Число 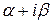является корнем характеристического уравнения кратности .

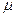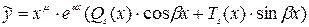
Пример 6. Найти частное решение дифференциального уравнения второго порядка, удовлетворяющего заданным начальным условиям

, , .

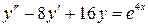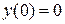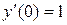Решение: Общее решение линейного неоднородного уравнения определяется равенством ,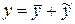

где 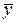− общее решение соответствующего однородного уравнения,

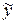− частное решение данного неоднородного уравнения.

1. Найдем 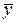− общее решение уравнения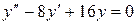

Составим характеристическое уравнение

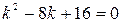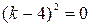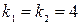Характеристическое уравнение имеет действительный двукратный корень, следовательно, общее решение однородного уравнения .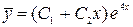

2. Найдем 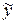− частное решение данного неоднородного уравнения

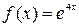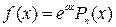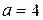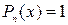Правая часть уравнения является частным случаем функции , где , − многочлен нулевой степени.

Число 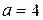является корнем характеристического уравнения кратности 2, тогда частное решение будем искать в виде

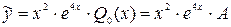Найдем 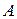методом неопределенных коэффициентов.

Найдем производные

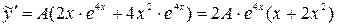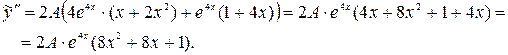
Подставим 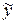, , 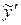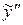в исходное уравнение и приравняем коэффициенты при одинаковых степенях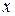

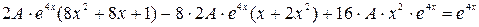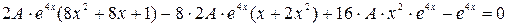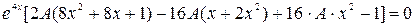Разделим обе части уравнения на 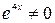, получим

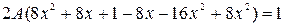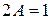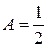Тогда частное решение .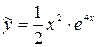

Общее решение неоднородного уравнения примет вид

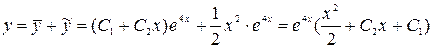3. Найдем частное решение данного уравнения, удовлетворяющее начальным условиям , .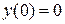

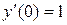Находим производную

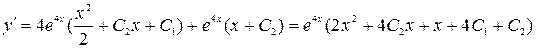
Используя заданные начальные условия составим систему

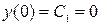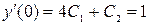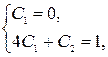
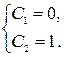
В итоге получим частное решение .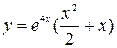

Ответ: .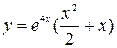

Числовые и функциональные ряды

I . Признаки сходимости числовых рядов

Рассмотрим числовой ряд

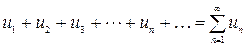(1)

Сумму первых 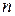членов числового ряда обозначают через 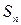и называют 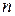-ной частичной суммой ряда:

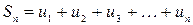Ряд называется сходящимся, если его 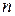-ная частичная сумма 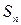при неограниченном возрастании 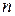стремится к конечному пределу, то есть, если

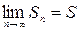Число 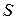называют суммой ряда. Если же 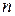-ная частичная сумма ряда при 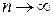не стремится к конечному пределу, то ряд называют расходящимся.

1) Необходимый признак сходимости. Если ряд (1) сходится, то общий член ряда 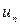стремится к нулю при 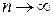. Если же 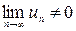, то ряд (1) расходится.

2) Признак Даламбера. Если для ряда (1) существует 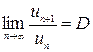, то этот ряд сходится при 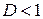и расходится при .

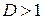3) Радикальный признак Коши. Если для ряда (1) существует 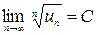, то этот ряд сходится при 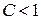и расходится при .

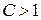4) Интегральный признак Коши. Если 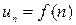, где функция 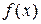положительна, монотонно убывает и непрерывна на промежутке 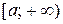, 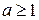то ряд (1) и интеграл 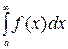сходятся или расходятся одновременно.

Пример 7 . Исследовать сходимость числового ряда:

а) 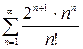; б) .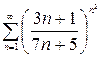

Решение:

а)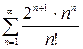

Воспользуемся признаком сходимости Даламбера.

Найдем .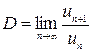

Так как 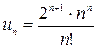, то 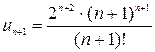. Получим

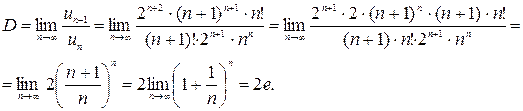
Так как 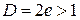, то заданный ряд расходится.

б)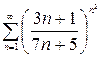

Воспользуемся радикальным признаком Коши. Найдем

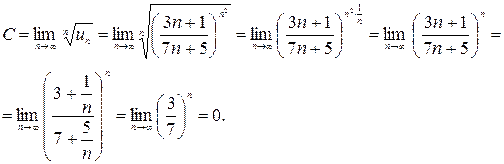
Так как 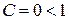, то заданный ряд сходится.

Ответ: а) ряд расходится;

б) ряд сходится.

Задача 7 . ( ) Исследовать сходимость числового ряда:

а) б)

Решение:

а)

Воспользуемся _________________________________________________

Найдем ______________________

Так как 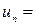, то 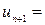. Получим

б)

Воспользуемся ____________________________________________

Найдем

Ответ: а)

б)

II . Знакочередующиеся ряды

Рассмотрим знакочередующийся ряд

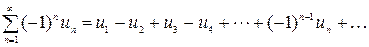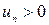, ( ) (2)

Признак Лейбница. Если для знакочередующегося ряда (2) выполнены условия:

1) 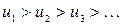и 2) ,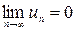

то ряд сходится.

Из абсолютных величин ряда (2) составим ряд

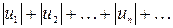(3)

Если ряд (3) сходится, то ряд (2) также сходится и называется абсолютно сходящимся. Если ряд (3) расходится, а ряд (2) сходится, то знакочередующийся ряд (2) называется условно сходящимся.

Пример 8 . Исследовать сходимость знакопеременного ряда и установить характер сходимости (абсолютная, условная)

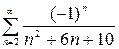Решение:

Запишем несколько первых членов заданного ряда

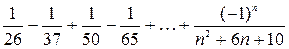
Данный ряд является знакочередующимся. По признаку Лейбница ряд сходится, так как выполняются следующие условия:

1) члены ряда убывают по абсолютной величине, так как

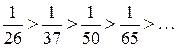
2) .

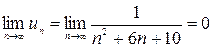Для проверки ряда на абсолютную и условную сходимость составим ряд из абсолютных величин заданного ряда. Получим знакоположительный ряд

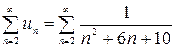Исследуем ряд на сходимость, используя интегральный признак Коши. Составим функцию 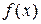так, чтобы 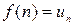. Для этого достаточно положить 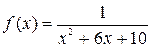. Функция 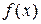определена, непрерывна, положительна и монотонно убывает на промежутке 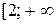). Найдем

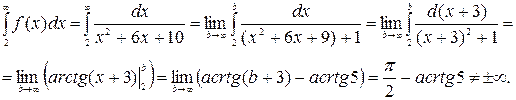
Вывод: интеграл сходится, а значит, сходится и ряд 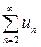. Следовательно, исходный ряд сходится абсолютно.

Ответ: ряд сходится абсолютно.

Задача 8 . ( ) Исследовать сходимость знакопеременного ряда и установить характер сходимости (абсолютная, условная).

Решение:

Запишем несколько первых членов заданного ряда

Данный ряд является ____________________________________________

По признаку Лейбница ряд __________________, так как выполняются следующие условия:

Для проверки ряда на абсолютную и условную сходимость составим ряд из абсолютных величин заданного ряда. Получим ряд

Исследуем ряд на сходимость, используя ___________________________ __________________________________________________________________

Составим функцию 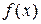так, чтобы ________________.

Для этого достаточно положить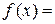

____________________________________________________________________________________________________________________________________

Найдем

Вывод: ________________________________________________________ __________________________________________________________________

Ответ:

III . Степенные ряды

Ряд вида

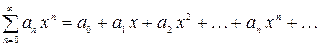(4)

называется степенным рядом.

Придавая переменной 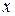в степенном ряде конкретное числовое значение 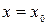, получим числовой ряд, который сходится или расходится. Множество всех тех значений переменной, при которых данный степенной ряд сходится, называется областью сходимости этого ряда.

При 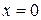всякий степенной ряд вида (4) сходится.

Интервалом сходимости действительного степенного ряда (4) называется такой интервал 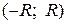, что в каждой его точке ряд сходится абсолютно, а в каждой точке, лежащей вне отрезка 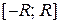, ряд расходится. На границах интервала сходимости, то есть, в точках 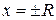ряд может как сходиться, так и расходиться. Число 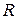называют радиусом сходимости степенного ряда.

Для вычисления радиуса сходимости 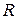степенного ряда применяется формула 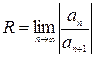или .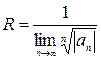

Пример 9. Найти интервал сходимости степенного ряда

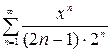Решение:

1. Найдем радиус сходимости данного степенного ряда по формуле

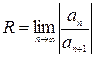Так как 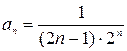, , 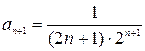получим

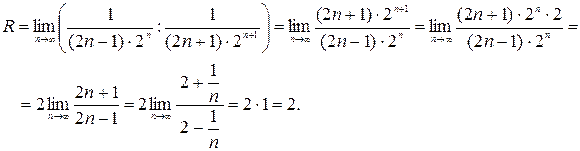
Значит, интервал сходимости ряда 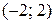. Исследуем сходимость ряда на концах интервала, то есть, в точках 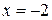и .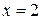

2. При 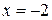получим знакопеременный ряд

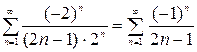Исследуем ряд на сходимость, используя признак Лейбница:

1) члены ряда убывают по абсолютной величине, так как

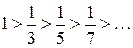
2) .

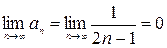Так как условия 1) и 2) теоремы Лейбница выполнены, то исходный ряд при 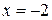сходится.

3. При 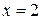получим знакоположительный ряд

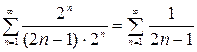Исследуем ряд на сходимость, используя интегральный признак Коши.

Положим 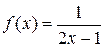. Вычислим неопределенный интеграл

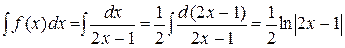Тогда несобственный интеграл будет равен

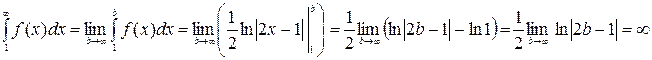Таким образом, интеграл расходится, следовательно, исходный ряд при 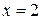расходится.

4. Вывод: область сходимости заданного ряда − промежуток .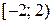

Ответ: .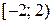

Задача 9. ( ) Найти интервал сходимости степенного ряда

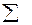
Решение:

1. Найдем радиус сходимости данного степенного ряда по формуле

Значит, интервал сходимости ряда ____________. Исследуем сходимость ряда на концах интервала, то есть, в точках _________ и __________

2. При 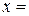____ получим _____________________________

Исследуем ряд на сходимость, используя _______________________________

3. При 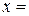____ получим ______________________________________

Исследуем ряд на сходимость, используя _______________________________

4. Вывод: ______________________________________________________

Ответ:

Список используемой литературы

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

дата ____________ подпись_______________

Контрольные вопросы

1. Что такое дифференциальное уравнение? Что значит решить дифференциальное уравнение.

2. Что называется порядком дифференциального уравнения?

3. Сформулируйте теорему Коши о существовании и единственности решения дифференциального уравнения I порядка.

4. Типы и методы решения дифференциальных уравнений I порядка.

5. Способы решения дифференциальных уравнений II порядка, допускающих понижение порядка.

6. Какое дифференциальное уравнение II порядка называется линейным однородным с постоянными коэффициентами? неоднородным?

7. Что такое числовой ряд? Какой ряд называется сходящимся? расходящимся?

8. Сформулируйте необходимый признак сходимости ряда.

9. Сформулируйте достаточные признаки сходимости знакопостоянных рядов.

10. Сформулируйте признак сходимости Лейбница для знакочередующихся рядов.

11. Какой ряд называется абсолютно сходящимся? условно сходящимся?

12. Функциональные и степенные ряды.

13. Что называется областью сходимости, радиусом сходимости степенного ряда?

Работа над ошибками

Дата добавления: 2022-06-11; просмотров: 33; Мы поможем в написании вашей работы!

Поделиться с друзьями:

Мы поможем в написании ваших работ!