Основы метода параметрического уранивания
Министерство образования и науки Российской федерации
Федеральное ГОСУДАРСТВЕННОЕ бюджетное ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»
Утверждено на заседании
кафедры прикладной геодезии
«13» октября 2014 г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к заданиям по дисциплине «Теория математической
обработки геодезических измерений» на тему:
Уравнивание нивелирных сетей параметрическим способом
для студентов 2-го курса очного и заочного по специальности 120400.65 «Прикладная геодезия» и направлению подготовки 120401.62 «Геодезия и дистанционное зондирование»
Ростов-на-Дону
2014
УДК 528.1
ББК 26.104
Методические указания по дисциплине "Теория математической обработки геодезических измерений". Уравнивание нивелирных сетей параметрическим способом / для студентов 2-го курса очного и эаочного по специальности 120400 «Прикладная геодезия» и направлению подготовки 120401 «Геодезия и дистанционное зондирование».- Ростов-на-Дону: Рост. гос. строит. ун-т, 2014.- 20 с.
В методических указаниях даны основы уравнивания геодезических сетей параметрическим способом. Приведена схема решения нормальных уравнений с использованием алгоритма Гаусса. Рассмотрен пример обработки нивелирной сети по методу наименьших квадратов. Разработаны варианты индивидуальных заданий для студентов.
|
|
|
УДК 528.1
Составители: к.т.н., доцент Губеладзе А.Р.
инженер Губеладзе И.О.
Рецензент: д-р техн. наук, проф. Пимшин Ю.И.
Редактор Н.Е. Гладких
Доп. план 2014 г., поз.
 Подписано в печать Формат 60х84/16. Бумага писчая. Ризограф.
Подписано в печать Формат 60х84/16. Бумага писчая. Ризограф.
Уч.-изд. л. Усл.-печ. л. Тираж 100 экз. Заказ

Редакционно-издательский центр
Ростовского государственного строительного университета
344022, Ростов н/Д., ул. Социалистическая, 162
© Ростовский государственный
Строительный университет, 2014
Основы параметрического способа уравнивания
Задачи и методы уравнивания
|
|
|
Для однозначного определения значений k неизвестных параметров необходимо и достаточно измерить k величин. Поскольку в геодезии существует принцип избыточности измерений, то число r = n - k, где n - число всех измеренных величин, является избыточным. При этом избыточные измерения должны находиться с необходимыми в функциональной зависимости. Наилучшее решение в процессе обработки результатов измерений получают согласно принципу наименьших квадратов, который состоит из следующего условия
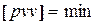 , (1)
, (1)
где р - веса измеренных величин;
v - поправки в измеренные значения.
Определение окончательных значений искомых величин при избыточных измерениях называют уравниванием, а эти же действия с соблюдением условия (1) - уравниванием по способу наименьших квадратов или строгим уравниванием.
Реализация метода наименьших квадратов позволяет решить следующие задачи:
1) исключается неопределенность решения, связанная с избыточным числом измерений;
2) повышается точность и надежность получаемых результатов за счет оптимального использования всех измерений;
3) выполняется оценка точности результатов измерений и полученных значений, также функций от них.
|
|
|
Строгое уравнивание может быть реализовано либо параметрическим, либо коррелатным способами или их разновидностями.
Обязательным условием уравнивания является возможность функционально выразить все измеренные величины через уравниваемые параметры.
В геодезической практике встречаются случаи, когда необходимо определить некоторые величины косвенным путем, причем эти величины должны быть связаны с измеряемыми функциональными зависимостями.
Основы метода параметрического уранивания
Предположим нам известны результаты измерений n величин x1, x2, ... , xn. Требуется определить надежные значения k величин T1, T2, ... , Tk, которые связаны с уравненными значениями X1, X2, ... , Xk измеренных величин определенными функциональными зависимостями:
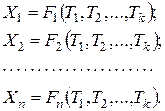 (2)
(2)
Равенства такого вида называются параметрическими уравнениями связи. Согласно (2) имеем
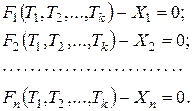 (3)
(3)
В случае, если имеют место результаты неравноточных измерений x1, x2, ... , xn , устанавливают веса p1 , p2 , ... , pn .
|
|
|
Уравненные значения измеренных величин будут
Xi = xi + vi , (4)
где vi - поправки в результаты измерений.
Тогда равенства (3) с учетом (4) примут вид
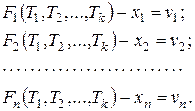 (5)
(5)
Полученные равенства называются уравнениями поправок в общем виде.
В системе (5) число неизвестных будет n + k > n , т.е. превысит число уравнений в системе, что приводит к неопределенности решения. Для нахождения неизвестных воспользуемся принципом наименьших квадратов. Определим значения T1, T2, ... , Tk при условии
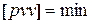 .
.
Сделаем замену неизвестных через приближенные значения tj и поправки к ним δ tj
Tj = tj + δ tj . (6)
Полученные значения неизвестных из (6) подставляем в уравнения системы (5). В результате чего получим
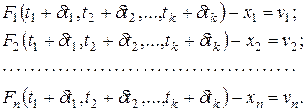 (7)
(7)
Нелинейные функции (7) необходимо привести к линейному виду, разложив в ряд Тейлора и ограничиваясь первыми степенями разложения
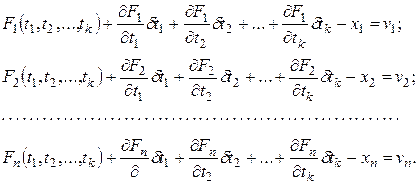 (8)
(8)
Введем следующие обозначения
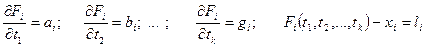 .
.
Подставив введенные обозначения в уравнения (8), получим уравнения поправок в линейном виде
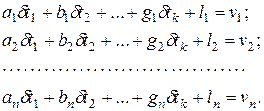 (9)
(9)
Для вычисления коэффициентов нормальных уравнений воспользуемся табличным способом (табл. 1).
Определение коэффициентов нормальных уравнений
Таблица 1
| № уравнения | a] | b] | … | g] | l] | s] | p | v | pv | pvv | plv |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | a1 | b1 | … | g1 | l1 | s1 | p1 | v1 | p1v1 | p1v1v1 | p1l1v1 |
| 2 | a2 | b2 | … | g2 | l2 | s2 | p2 | v2 | p2v2 | p2v2v2 | p2l2v2 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| n | an | bn | … | gn | ln | sn | pn | vn | pnvn | pnvnvn | pnlnvn |
| Суммы | [a] | [b] | … | [g] | [l] | [s] | [v] | [pv] | [pvv] | [plv] | |
| Неизвест. | δt1 | δt2 | … | δtk | |||||||
| [pa | [paa] | [pab] | … | [pag] | [pal] | [pas] | |||||
| [pb | [pbb] | … | [pbg] | [pbl] | [pbs] | ||||||
| … | … | … | … | … | … | … | |||||
| [pg | [pgg] | [pgl] | [pgs] | ||||||||
| [pl | [pll] | [pls] | |||||||||
| [ps | [pss] |
В результате получаем коэффициенты и свободные члены нормальных уравнений в параметрическом способе уравнивания:
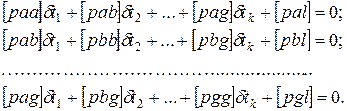 (10)
(10)
При заполнении верхней части таблицы выполняется контроль сумм:
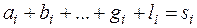 , (11)
, (11)
а в нижней части данной таблицы
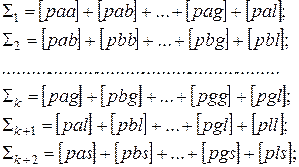 (12)
(12)
Контролем будут следующие выражения:
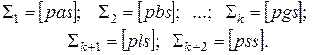 (13)
(13)
Решение нормальный уравнений осуществляется согласно схеме Гаусса- Дулитля (табл. 2).
При решении нормальных уравнений выполняют следующие виды контроля: промежуточный и по [pvv]. Промежуточный контроль – это суммарный контроль и делается в схеме Гаусса-Дулитля согласно формулам (12) и (13) в процессе решения нормальных уравнений (табл. 2).
Контролем по [pvv] являются следующие равенства:
- в табл. 2 при решении нормальных уравнений в графах 4 и 5
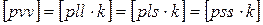 , (14)
, (14)
где
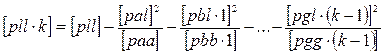 ;
;
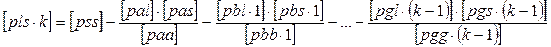 ;
;
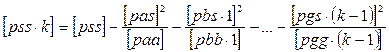 ;
;
- в табл. 1 после нахождения поправок vi в измеренные значения
 . (15)
. (15)
Таким образом, значение [pvv] определяется на различных этапах уравнивания в параметрическом способе и является сквозным контролем уравнительных вычислений. Заключительный контроль осуществляется подстановкой уравненных значений измеренных величин и найденных неизвестных в равенства (3).
| δ t1 | δ t2 | δ t3 | l | s | Контроль |
| 1 | 2 | 3 | 4 | 5 | 6 |
[paa]
-1
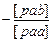
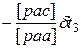 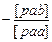 δ t2
δ t1 δ t2
δ t1
| [pab]
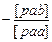 [pbb]
[pbb]
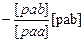 [pbb·1]
-1
[pbb·1]
-1
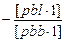
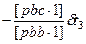 δ t2 δ t2
| [pac]
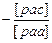 [pbc]
[pbc]
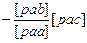 [pbc·1]
[pbc·1]
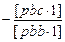 [pcc]
[pcc]
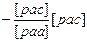
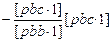 [pcc·2]
-1 [pcc·2]
-1
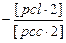 δ t3
δ t3
| [pal]
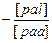 [pbl]
[pbl]
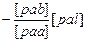 [pbl·1]
[pbl·1]
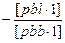 [pcl]
[pcl]
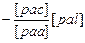
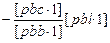 [pcl·2] [pcl·2]
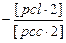 [pll]
[pll]
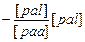
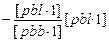 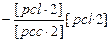 [pll·3] [pll·3]
| [pas]
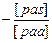 [pbs]
[pbs] 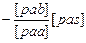 [pbs·1]
[pbs·1]
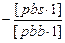 [pcs]
[pcs]
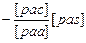 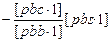 [pcs·2] [pcs·2]
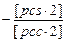 [pls]
[pls]
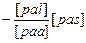
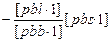 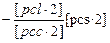 [pls·3] [pls·3]
| Σ1
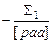 Σ2
Σ2
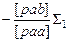 [Σ2·1]
[Σ2·1]
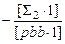 Σ3
Σ3
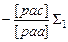
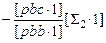 [Σ3·2] [Σ3·2]
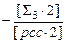
|
Схема решения нормальных уравнений Гаусса-Дулитля
Таблица 2
Дата добавления: 2022-06-11; просмотров: 27; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
