Найти частные производные самостоятельно, а затем посмотреть решения
Понятие частной производной
Каждая частная производная (по x и по y) функции двух переменных представляет собой обыкновенную производную функции одной переменной при фиксированном значении другой переменной:
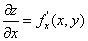(где y = const),
(где x = const).
Если тяжело сосредоточиться, чтобы отслеживать, где в функции константа, то можно в черновом решении примера вместо переменной с фиксированным значением подставить любое число - тогда можно будет быстрее вычислить частную производную как обыкновенную производную функции одной переменной. Надо только не забыть при чистовом оформлении вернуть на место константу (переменную с фиксированном значением).
Пример 1. Найти частные производные функции
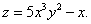
Решение. Находим частную производную по переменной "икс" (табличная производная 3):
(y фиксировано);
Находим частную производную по переменной "игрек" (тоже производная 3 в таблице производных):
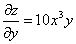(x фиксировано).
Как видно, не имеет значения, в какой степени переменная, которая фиксирована: в данном случае это просто некоторое число, являющееся множителем (как в случае обычной производной) при переменной, по которой находим частную производную. Если же фиксированная переменная не умножена на переменную, по которой находим частную производную, то эта одинокая константа, безразлично, в какой степени, как и в случае обычной производной, обращается в нуль.
|
|
|
Пример 2. Дана функция
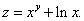
Найти частные производные
(по иксу) и 
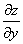(по игреку) и вычислить их значения в точке А (1; 2).
Решение. При фиксированном y производная первого слагаемого находится как производная степенной функции (таблица производных функций одной переменной):
.
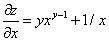При фиксированном x производная первого слагаемого находится как производная показательной функции (формула 17 в таблице производных), а второго – как производная постоянной (формула 1):
.
Теперь вычислим значения этих частных производных в точке А (1; 2):
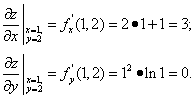
Пример 3. Найти частные производные функции
.
Решение. В один шаг находим
(y фиксировано и является в данном случае множителем при x, как если бы аргументом синуса было 5x: точно так же 5 оказывается перед знаком функции);
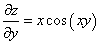
(x фиксировано и является в данном случае множителем при y).
Аналогично определяются частные производные функции трёх и более переменных.
Если каждому набору значений (x; y; ...; t) независимых переменных из множества D соответствует одно определённое значение u из множества E, то u называют функцией переменных x, y, ..., t и обозначают u = f(x, y, ..., t).
Для функций трёх и более переменных геометрической интерпретации не существует.
Частные производные функции нескольких переменных определяются и вычисляются также в предположении, что меняется только одна из независимых переменных, а другие при этом фиксированы.
|
|
|
Пример 4. Найти частные производные функции
.
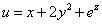Решение. y и z фиксированы:
,
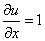x и z фиксированы:
,
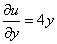x и y фиксированы:
Найти частные производные самостоятельно, а затем посмотреть решения
Пример 5. Найти частные производные функции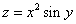 
.
Пример 6. Найти частные производные функции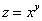 
.
Пример 7. Найти частные производные функции 
.
Частная производная функции нескольких переменных имеет тот же механический смысл, что и производная функции одной переменной, - это скорость изменения функции относительно изменения одного из аргументов.
Пример 8. Количественная величина потока П пассажиров железных дорог может быть выражена функцией
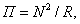
где П – количество пассажиров, N – число жителей корреспондирующих пунктов, R – расстоянии между пунктами.
Частная производная функции П по R, равная
показывает, что уменьшение потока пассажиров обратно пропорционально квадрату расстояния между корреспондирующими пунктами при одной и той же численности жителей в пунктах.
Частная производная П по N, равная
|
|
|
показывает, что увеличение потока пассажиров пропорционально удвоенному числу жителей населённых пунктов при одном и том же расстоянии между пунктами.
Полный дифференциал
Произведение частной производной на приращение соответствующей независимой переменной называется частным дифференциалом. Частные дифференциалы обозначаются так:
и т.д.
Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Для функции двух независимых переменных полный дифференциал выражается равенством
(7)
Пример 9. Найти полный дифференциал функции
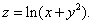
Решение. Результат использования формулы (7):
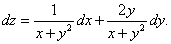
Функция, имеющая полный дифференциал в каждой точке некоторой области, называется дифференцируемой в этой области.
Дата добавления: 2022-06-11; просмотров: 13; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!