Математические операции с матрицами и векторами
linsolve(M,v) решение линейной системы алгебраических уравнений вида M∙x=v, где M – матрица.
gausselim(M) метод Гаусса для матрицы M.
eigenvals(M) вычисление собственных чисел матрицы M.
eigenvects(M) вычисление собственных векторов матрицы M; результат представляется в виде: собственное число, его кратность, затем соответствующий собственный вектор.
norm(M) вычисление нормы матрицы M.
orthog(M) проверка ортогональности матрицы M.
hermite(M,x) получение эрмитовой формы матрицы M.
angle(v1,v2) вычисление угла между векторами v1 и v2 одинаковой длины.
basis(V) определение базиса для набора векторов V.
rank(M) вычисление ранга матрицы M.
Команды работы со структурой матриц и векторов
rowdim(M) число строк матрицы M.
coldim(M) число столбцов матрицы M.
vectdim(v) число элементов вектора v.
addcol(M,i1,i2,expr) формирование новой матрицы, получаемой из матрицы M прибавлением к столбцу i2 столбца i1, умноженного на выражение expr.
addrow(M,i1,i2,expr) аналогична addcol, только для работы со строками матрицы M.
row(M,i) выделение i-ой строки из матрицы M.
col(M,j) выделение j-го столбца из матрицы M.
сoncat(M1,M2) cлияние матриц M1 и M2.
submatrix(M,i1..i2,j1..j2) выделение подматрицы из матрицы M со строками от i1 до i2 и столбцами от j1 до j2.
subvector(v,i..j) выделение подвектора из v с элементами v[i],...,v[j].
delrows(M,i..j) уничтожение столбцов с номерами от i до j у матрицы M.
delcols(M,i..j) уничтожение строк с номерами от i до j у матрицы M.
Примеры применения некоторых команд линейной алгебры
|
|
|
Поясним работу некоторых из перечисленных команд следующими примерами.
> with(linalg):
> M:=matrix(3,3,[[1,2,3],[4,5,6],[7,8,9]]);

> det(M);
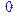
(Отметим здесь, что идентификатор M и m – это разные объекты !).
> rank(M);
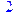
Добавление 1 к диагональным элементам матрицы M:
> M:=evalm(M+1);

Вычисление обратной к M матрицы (здесь в качестве матрицы M берется матрица с диагональными элементами, увеличенными на 1 по сравнению с первоначально определенной матрицей):
> A:=evalm(1/M);
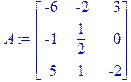
Проверка правильности определения обратной матрицы:
> B:=evalm(M &* A);

Матрица B – единичная матрица, т.е. обратная матрица определена правильно.
Задание вектора v с элементами x,y,z:
> v:=array(1..3,[x,y,z]);

Умножение матрицы M на вектор v:
> u:=multiply(M,v);

Определение размерности вектора v:
> vectdim(u);
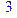
Вычисление cкалярного произведения векторов v и u:
> f:=dotprod(u,v);

> simplify(f);

Основные операции векторного анализа
Gradient(v,x) вычисление градиента вектора v по совокупности переменных x.
Divergence(f,x) вычисление дивергенции функции f по совокупности переменных x.
Curl(v,x) вычисление ротора трехмерного вектора v по трем переменным x.
Laplacian(f,x) вычисление Лапласиана функции f по совокупности переменных x.
|
|
|
Jacobian(v,x) вычисление матрицы Якоби для вектора v по совокупности переменных x.
Приведем некоторые простые примеры:
Подключение необходимой библиотеки и определение рабочей (декартовой) системы координат (x1,y1,z1):
> with(VectorCalculus): SetCoordinates( 'cartesian'[x1,y1,z1] );

Вычисление градиента функции t:
> t := x1^2*y1^2*z1^2;

> r:=Gradient(t);
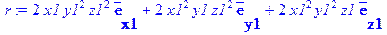
Задание векторного поля F и вычисление его дивергенции:
> F := VectorField( <x1^2,y1^2,z1^2> );
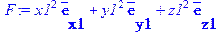
> r:=Divergence( F );

Задание векторного поля F и вычисление его ротора:
> F := VectorField( <y1*z1,-x1,z1*x1*y1> );

> r:=Curl( F );

Задание функции f и вычисление оператора Лапласа от нее:
> f:=x1^2+y1^2+z1^2;

> t:=Laplacian( f, [x1,y1,z1] );
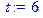
Задание векторного поля F и вычисление для него матрицы Якоби:
> F := VectorField( <x1^2+z1^3,y1^2,z1^2+x1*y1> );
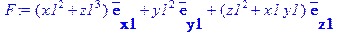
> M:=Jacobian(F,[x1,y1,z1]);

Дата добавления: 2022-06-11; просмотров: 17; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
