Свободные незатухающие колебания.
Лекция 5. «Колебания»
Гармонические колебания. Векторная диаграмма. Сложение гармонических колебаний одного направления равных и близких частот. Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот. Свободные незатухающие колебания. Энергия и импульс гармонического осциллятора. Фазовая траектория. Физический маятник. Квазиупругая сила.
Положение равновесия и квазиупругая сила.
Рассмотрим одномерное движение тела под действием консервативной силы вдоль оси X. Для потенциальной энергии тела вблизи некоторой точки x0 можно записать выражение
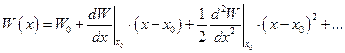
Потенциальная энергия и вектор консервативной силы связаны соотношением:
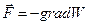 ,
,
откуда для проекции силы на ось X получаем: 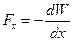 , т.е.
, т.е.
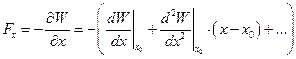 .
.
 Далее будем предполагать, что точка x0 является положением равновесия, поэтому должно выполняться условие
Далее будем предполагать, что точка x0 является положением равновесия, поэтому должно выполняться условие 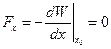 , тогда для изменения потенциальной энергии вблизи точки x0 имеем:
, тогда для изменения потенциальной энергии вблизи точки x0 имеем: 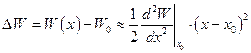 и для проекции силы:
и для проекции силы: 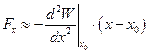 .
.
Рассмотрим случай, когда в точке x0 наблюдается локальный минимум потенциальной энергии. Тогда 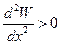 и существует некоторая окрестность точки U(x0), для которой выполняется условие
и существует некоторая окрестность точки U(x0), для которой выполняется условие 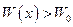 и
и 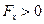 при
при 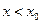 ,
, 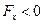 при
при 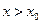 , то есть в этой окрестности вектор силы, действующей на тело, будет направлен к точке x0. А это значит, что при малых смещениях тела из положения равновесия, сила будет стремиться вернуть тело обратно. Такое положение равновесия называется устойчивым.
, то есть в этой окрестности вектор силы, действующей на тело, будет направлен к точке x0. А это значит, что при малых смещениях тела из положения равновесия, сила будет стремиться вернуть тело обратно. Такое положение равновесия называется устойчивым.
|
|
|
Положение равновесия называется неустойчивым, если при малом отклонении от этого положения возникает сила, стремящаяся увести тело от положения равновесия. Очевидно, в этом случае в точке x0 наблюдается локальный максимум потенциальной энергии 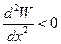 .
.
В случае, когда 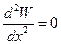 требуется дополнительное исследование.
требуется дополнительное исследование.
Итак, выражение для консервативной силы вблизи положения устойчивого равновесия можно записать в векторной форме: 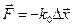 , а величину потенциальной энергии
, а величину потенциальной энергии 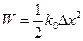 + const, где
+ const, где 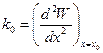 . Такая форма записи для консервативной силы вблизи точки равновесия называется квазиупругой силой.
. Такая форма записи для консервативной силы вблизи точки равновесия называется квазиупругой силой.
Запишем второй закон Ньютона для тела, движущегося под действием квазиупругой силы вблизи точки устойчивого положения равновесия:
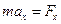 , где
, где 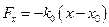 .
.
Введём ось Х так, чтобы 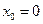 , тогда уравнение движения примет вид:
, тогда уравнение движения примет вид: 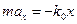 . С учётом зависимости
. С учётом зависимости 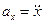 это уравнение примет вид:
это уравнение примет вид: 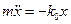 или
или
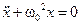 ,
,
где 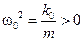 . Это линейное обыкновенное дифференциальное уравнение второго порядка.
. Это линейное обыкновенное дифференциальное уравнение второго порядка.
Решением этого уравнения являются гармонические функции от времени t:
|
|
|
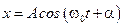 или
или 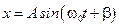 ,
,
описывающие смещение тела от положения равновесия (точка 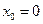 ).
).
Замечание. Обе формы записи равноправны. Например, одна переходит в другую при 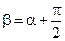 .
.
Так как гармонические функции синус и конус имеют период 2p, то параметры процесса будут повторяться через минимальный промежуток времени Т, называемый периодом:
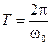 .
.
Таким образом, уравнение
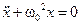
описывает колебательный процесс, параметры которого не изменяются с течением времени. Этот процесс принято называть свободными незатухающими колебаниями.
Учитывая, что величина 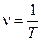 называется частотой колебаний (единица измерения Гц - Герц), то величину
называется частотой колебаний (единица измерения Гц - Герц), то величину 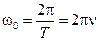 называют круговой или циклической частотой колебаний (единица измерения с-1).
называют круговой или циклической частотой колебаний (единица измерения с-1).
Величина А – амплитуда колебаний- это модуль максимального смещения. По определению A > 0 – всегда положительная величина. Аргумент гармонической функции 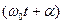 называется фазой колебания, а величина a называется начальной фазой колебаний - это фаза колебаний в момент времени t = 0, который обычно называют начальным моментом времени.
называется фазой колебания, а величина a называется начальной фазой колебаний - это фаза колебаний в момент времени t = 0, который обычно называют начальным моментом времени.
|
|
|
В этом колебательном процессе с течением времени сохраняется величина механической энергии: 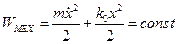 . Действительно:
. Действительно:
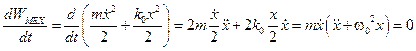 .
.
Свободные незатухающие колебания.
Колебания – движения или состояния, параметры которых повторяются во времени. Колебания в той или иной мере встречаются во всех явлениях природы: от пульсации излучения звёзд, движения планет до внутриклеточных процессов или колебаний атомов и молекул, колебаний полей.
В физике особо выделяют механические и электромагнитные колебания (и их комбинации).
Моделью для изучения механических колебаний является осциллятор – материальная точка или система, совершающая колебательное периодическое движение около положения устойчивого равновесия. (Более того, термин осциллятор применим к любой системе, если описывающие её величины периодически меняются во времени.) Простейшие примеры осцилляторов – грузик на пружине, маятник.
 Пример. Груз массы m подвешен на невесомой пружине жесткости k в поле сил тяжести (пружинный маятник). Найти период его колебаний. Сопротивлением воздуха пренебречь.
Пример. Груз массы m подвешен на невесомой пружине жесткости k в поле сил тяжести (пружинный маятник). Найти период его колебаний. Сопротивлением воздуха пренебречь.
Решение. Запишем уравнение его движения в проекции на вертикальное направление Y:
|
|
|
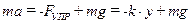 или
или 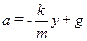 .
.
где y – величина растяжения пружины. Положение равновесия груза на пружине: 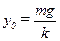 . Введём смещение x груза от положения равновесия:
. Введём смещение x груза от положения равновесия: 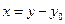 , тогда
, тогда 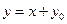 ,
, 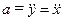 .
.
Получаем уравнение: 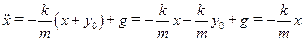 ,
, 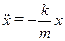 . Перенесём в последнем соотношении все слагаемые в левую часть и вспомним, что дифференциальное уравнение, описывающее свободные незатухающие колебания, имеет вид:
. Перенесём в последнем соотношении все слагаемые в левую часть и вспомним, что дифференциальное уравнение, описывающее свободные незатухающие колебания, имеет вид: 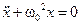 .
.
Тогда у нас 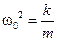 и тогда период колебаний
и тогда период колебаний 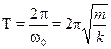 .
.
Механическая энергия груза на пружине: 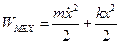 .§
.§
Пример. Найдем период колебаний математического маятника - материальной точки массы m, подвешенной на невесомой нерастяжимой нити длиныl .
 Решение. Рассмотрим движение маятника в тот момент, когда он поднимается. Отклонение нити от вертикали зададим угловой координатой j. При этом, если угол j увеличивается (против часовой стрелки), то касательное ускорение точки направлено против направления движения. Поэтому уравнение движения имеет вид:
Решение. Рассмотрим движение маятника в тот момент, когда он поднимается. Отклонение нити от вертикали зададим угловой координатой j. При этом, если угол j увеличивается (против часовой стрелки), то касательное ускорение точки направлено против направления движения. Поэтому уравнение движения имеет вид:
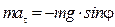 .
.
Вблизи положения равновесия проекция силы тяжести должна быть представлена как квазиупругая сила. Если выполняется условие малости колебаний, то 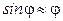 , поэтому длина дуги окружности
, поэтому длина дуги окружности 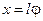 , следовательно, проекция силы тяжести
, следовательно, проекция силы тяжести 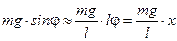 . Поэтому коэффициент в выражении для квазиупругой силы
. Поэтому коэффициент в выражении для квазиупругой силы 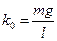 . Касательное ускорение связано с угловым ускорением соотношением
. Касательное ускорение связано с угловым ускорением соотношением 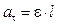 (где
(где 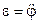 ), поэтому, после сокращения массы m получим:
), поэтому, после сокращения массы m получим:
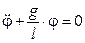 .
.
С учетом выражения для циклической частоты 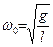 период колебаний имеет вид:
период колебаний имеет вид: 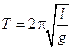 . Механическая энергия математического маятника равна:
. Механическая энергия математического маятника равна:
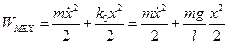 .
.
При движении по окружности 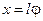 ,
, 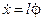 , поэтому
, поэтому
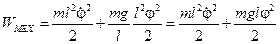 .
.
Дата добавления: 2022-01-22; просмотров: 225; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
