Построение характеристического многочлена матрицы

Лекция №6

Собственные значения

Постановка проблемы собственных значений

Напомним постановку проблемы собственных значений из курса линейной алгебры. Если A — квадратная матрица n´n и Ax = l x при x ¹ 0, то число l называется собственным значением матрицы, а ненулевой вектор x — собственным вектором. Перепишем задачу на собственные значения в стандартном виде

(A - l E)x= 0, x ¹ 0, (1)

где E — единичная матрица размером n´n.

Для существования нетривиального собственного значения должно выполняться уравнение

det(A - l E) = 0. (2)

Уравнение (2) представляет собой полином степени n от l, его еще называют характеристическим многочленом или вековым уравнением. Поскольку уравнение (2) является полиномом степени n, постольку существует n собственных значений l _i, i = 1,…,n — корней характеристического многочлена, которые могут не быть разными, т.е. могут быть кратными.

Перепишем уравнение (2) в форме полинома:

. (2¢)

Если найдено некоторое собственное значение, то, после подстановки его в (1), можно найти соответствующий собственный вектор. Будем в дальнейшем нормировать собственные вектора на единицу, т.е. предполагать, что этот вектор поделен на одну из своих норм. В этом случае каждому простому (не кратному) собственному значению отвечает один собственный вектор, а совокупность всех таких собственных векторов линейно независима. Отсюда следует, что, если все собственные значения матрицы являются простыми, то она имеет n линейно независимых векторов, образующих базис в n-мерном векторном пространстве.

Говорят о полной проблеме собственных значений, если требуется определить все собственные значения и собственные векторы матрицы A. Говорят о частичной проблеме собственных значений, если требуется найти лишь некоторые из собственных значений. К такой часто возникающей частичной проблеме относится задача нахождения максимального и минимального собственного значений. Обобщенная проблема собственных значений возникает при решении системы , а общая — когда элементы матрицы A зависят от l.

Каждому собственному значению кратности p может отвечать от 1 до p линейно независимых собственных векторов.

Приведем пример четырех матриц, у которых одно-единственное собственное значение l = a кратности 4.

Пример матриц четвертого порядка с одним и тем же собственным значением l = a кратности 4
Матрица	Собственные вектора

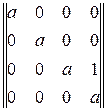
В таблице — линейно независимые нормированные собственные векторы, которые имеют следующий вид:

Четвертую матрицу в таблице называют простой жордановой (или классической) подматрицей. Третья матрица имеет так называемую каноническую жорданову форму, в которой по диагонали стоят либо числа, либо жордановы подматрицы, а все остальные элементы матрицы нули.

Задача на собственные значения может быть легко решена для матриц простой формы. К ним относятся диагональные, трехдиагональные, треугольные матрицы. Так, например, определитель треугольной или диагональной матрицы есть произведение диагональных элементов, но матрица A - l E также является треугольной или диагональной, поэтому собственные значения равны диагональным элементам треугольной или диагональной матриц. Легко проверить, что диагональная матрица имеет n собственных векторов , i = 1,…,n, которым соответствуют n собственных значений , i = 1,…,n.

Многие численные методы решения задач на собственные значения основаны на приведении матрицы к одному из перечисленных выше форм с помощью преобразования подобия.

Матрица B называется подобной матрице A, если существует обратимая матрица F такая, что B = F^-¹AF. Исходя и равенства Ax = l x, преобразуем его к виду:

, (3)

где y — собственный вектор матрица B. Таким образом, согласно (3), при преобразовании подобия собственные значения не меняются, а собственные векторы преобразуются по определенному закону.

Напомним некоторые определения специальных матриц.

Матрица B называется эрмитово сопряженной матрице A, если B получена путем транспонирования и комплексного сопряжения матрицы A, т.е. . В другом виде B = A^H. Матрица называется эрмитовой, если она эрмитово сопряжена себе, т.е. A = A^H. Матрица называется косоэрмитовой, если верно равенство A = - A^H. Вещественная эрмитова матрица называется симметричной, а косоэрмитова — кососимметричной. Унитарной называется матрица, обратная своей эрмитовой, т.е. U^H = U^-¹. Вещественные унитарные матрицы называются ортогональными. Матрица называется нормальной, если она перестановочна со своей эрмитово сопряженной, т.е. AA^H = A^HA. Легко проверить, что эрмитовые, косоэрмитовые и унитарные матрицы являются нормальными.

Особенно удобны преобразования подобия при помощи унитарных матриц, т.к. они свойство ортонормированности базиса не меняют. Если подобно преобразовать эрмитову матрицу с помощью унитарного преобразования, то получится также эрмитова матрица. Если нормальная матрица преобразуется подобно с помощью унитарной матрицы, то получается также нормальная матрица. Последние два утверждения предлагается доказать самостоятельно.

Известно, что для любой матрицы A есть такое унитарное преобразование U, что матрица U^HAU является верхней треугольной. Если A — нормальная матрица, то унитарное преобразование U преобразует ее к диагональной форме.

В MATLAB есть стандартная функция schur, которая произвольную квадратную матрицу A представляет в виде произведения UTU¢, где U¢ — обозначение MATLAB эрмитово сопряжения, а T — верхняя треугольная матрица. Эта операция называется разложением Шура, когда A = UTU¢. На листинге_№1 приведена форма обращения к функции schur.

Листинг_№1

%Программа тестирования разложения Шура

%очищаем рабочее пространство

clear all

%определяем максимальный порядок

%тестируемой матрицы A

nmax=500;

k=1;

%организуем цикл по тестированию

%матриц A различных порядков

for n=1:10:nmax

%генерируем случайную матрицу

%порядка n, элементы которой

%распределены по нормальному закону

A=randn(n);

%производим разложение Шура

[U T]=schur(A,’complex’);

%оцениваем ошибку разложения

error(k)=norm(A-U*T*U');

x(k)=n;

k=k+1;

end

%рисуем зависимость ошибки разложения

%от порядка матрицы

plot(x,error);

На рис.1 приведен график ошибки разложения Шура в зависимости от порядка матрицы. В целом можно констатировать отличную точность разложения для матриц, порядок которых не превышает 500. Для матриц более высокого порядка требуются специальные исследования.

Рис.1. График зависимости ошибки разложения Шура
от порядка матрицы

Не всякую матрицу с кратными собственными значениями можно преобразовать к диагональной форме, но она обязательно может быть преобразована к канонической жордановой форме. Если же матрица имеет только простые собственные значения, то существует преобразование подобия не обязательно унитарное, которое приводит матрицу к диагональной форме.

Устойчивость

Для исследования устойчивости проблемы собственных значений наряду с матрицей A необходимо рассмотреть эрмитово сопряженную матрицу A^H. Поскольку эрмитово сопряжение складывается из транспонирования и комплексного сопряжения, а характеристический многочлен включает определитель матрицы A - l E, который, как известно, не меняется при транспонировании, то оказывается, что . Из последнего равенства следует, что, если l собственное значение матрицы A, то l ^* — собственное значение матрицы A^H. Другими словами, собственные значения эрмитово сопряженных матриц комплексно сопряжены друг другу.

Введем обозначения для собственных векторов {x_i} и {y_j} матриц A и A^H соответственно. Покажем, что собственные векторы эрмитово сопряженных матриц, принадлежащих разным собственным значениям, ортогональны. Действительно, по определению имеем

. (3)

Скалярно умножим© первое уравнение слева на y_j, а второе — справа на x_i, тогда, после вычитания одного уравнения из другого, найдем

. (4)

Левая часть уравнения (4) равна нулю в силу определения скалярного произведения и эрмитово сопряжения, а правая часть преобразуется к виду , откуда следует, что

, (5)

что и требовалось доказать.

Таким образом, у эрмитовых матриц собственные значения вещественны и, поскольку , согласно (5), собственные векторы, принадлежащие разным собственным значениям, ортогональны.

Перейдем к проблеме устойчивости собственных значений и собственных векторов, ограничиваясь случаем, когда собственные векторы образуют базис, а некоторое собственное значение l _i простое. Варьируя основное уравнение Ax_i = l _i x_i, находим, с точностью до бесконечно малых вариаций более высокого порядка,

. (6)

Разложим поправку к собственным векторам по невозмущенным собственным векторам, т.е. запишем представление

. (7)

Поскольку вектор определен с точностью до константы, постольку всегда можно подобрать константу так, чтобы диагональные элементы разложения (7) были нулевыми, т.е. . В этом можно убедиться, записав представление

и поделив его на .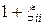

Подставим теперь разложение (7) в (6) и далее последовательно умножаем скалярно слева полученное уравнение на y_i и y_j соответственно, тогда, учитывая условие , находим

. (8)

Из приближенных равенств (8) можно сделать следующие оценки

(9)

где

так называемый i-й коэффициент перекоса матрицы, а j _i — угол между соответствующими собственными векторами матрицы A и эрмитово сопряженной ей A^H.

Для эрмитовой матрицы, как было установлено выше, все коэффициенты перекоса равны единице, поскольку , т.е. собственные значения эрмитовых матриц мало чувствительны к возмущениям элементов матрицы.

Для минимальной жордановой матрицы имеем

. (10)

Согласно примеру в (10), , коэффициент перекоса k₁ обращается в бесконечность, т.е. от неэрмитовых матриц следует ожидать сильной зависимости собственных значение и собственных векторов от возможных возмущений элементов матрицы.

На базе оценки (9) можно сделать следующие выводы. Собственное значение устойчиво относительно вариации матричных элементов, если соответствующий коэффициент перекоса мал, если он велик, то может оказаться, что устойчивость отсутствует. Собственный вектор устойчив к вариациям элементов матрицы, если все коэффициенты перекоса малы и данное собственное значение является простым.

В качестве примера, иллюстрирующего наличие неустойчивости в численной оценке собственных значений, рассмотрим неэрмитову матрицу A размером n´n незначительно возмущенную, путем добавления к элементу матрицы в левом нижнем углу малого числа e. Определим такую матрицу в следующем виде:

(11)

Матрица (11) является неэрмитовой, собственные значения которой без учета малого возмущения известны и равны 1,…,n. Далее средствами MATLAB найдем максимальное и минимальное собственные значения матрицы (11). Вычислим комбинацию ratio = , которая, без учета возмущения, должна равняться 1 при различных значениях порядка матрицы n.

На листинге_№2 приведен код соответствующе программы. На рис.2 итог работы программы представлен в виде графика зависимости комбинации ratio от порядка матрицы (11).

Листинг_№2

%Программа изучения устойчивости собственных

%значений матрицы на примере одной

%неэрмитовой матрицы

%очищаем рабочее пространство

clear all

%задаем максимальный порядок изучаемой матрицы

nmax=50;

%организуем цикл расчетов для различных

%порядков матрицы

for n=1:nmax

%формируем матрицу A

%вначале заполняем ее нулями

A=zeros(n);

%на главную диагональ загружаем числа:

%n, n-1,...,2,1

for i=1:n

A(i,i)=n+1-i;

end

%на соседнюю диагональ к главной диагонали

%загружаем числа n,...,n

if n~=1

for i=1:(n-1)

A(i,i+1)=n;

end

%возмущаем матрицу A, помещая в ее крайнем

%нижнем левом углу небольшое число eps

eps=1e-5;

A(n,1)=eps;

end

%находим собственные значения матрицы A

x=eig(A);

%находим отношение максимального собственного

%значения к минимальному, которое, согласно

%построенной (невозмущенной) матрице, должно

%равняться n

ratio(n)=max(abs(x))/min(abs(x));

%нормируем отношение собственных значений на n

ratio(n)=ratio(n)/n;

end

%рисуем график зависимости нормированного отношения

%собственных значений от порядка матрицы

plot(1:nmax,ratio);

Отношение ratio при e = 0 должно равняться 1, в чем можно убедиться непосредственно, полагая в программе соответствующее возмущение нулевым. Наличие возмущения приводит к резкой неустойчивости в численной оценке собственных значений и уже, начиная с порядка матрицы 10 говорить о какой либо близости к невозмущенным собственным значениям не приходится.

Рис.2. Зависимость отношения ratio от порядка матрицы

Построение характеристического многочлена матрицы

Для решения полной проблемы собственных значений можно исходить из следующей логики. Начинаем с развертывания векового определителя (2) или построения характеристического многочлена матрицы (2¢) далее находим все корни характеристического полинома, которые есть собственные значения. В данном пункте остановимся на проблеме развертывания векового определителя с помощью метода Данилевского и метода интерполяции.

В методе Данилевского исходная матрица A с помощью преобразований подобия F = S^-¹AS приводится к канонической форме Фробениуса:

. (12)

Разложим определитель матрицы F - l E по элементам первой строки, тогда

, (13)

т.е. первая строка матрицы Фробениуса составлена из коэффициентов характеристического многочлена, а, поскольку матрица Фробениуса подобна исходной матрице, постольку характеристические многочлены у них одинаковы.

В среде MATLAB функция poly(A) возвращает вектор-строку коэффициентов p = (1,- p₁,- p₂,…,- p_n) характеристического уравнения матрицы A. Функция compan(p) возвращает матрицу Фробениуса по вектор-строке коэффициентов характеристического многочлена p.

Переход от матрицы A к матрице Фробениуса F происходит за n - 1 преобразований подобия, при которых матрица последовательно преобразуется в матрицу Фробениуса построчно, начиная с последней строки матрицы A и кончая второй строкой.

Представим схему преобразования. Пусть проведено k - 1 преобразований подобия, применение которых к матрице A дало матрицу B_k _-₁:

При построении k-го преобразования подобия необходимо добиться того, чтобы k-я строка матрицы B_k стала k-й строкой матрицы Фробениуса. Для этого k - 1-й столбец матрицы B_k _-₁ делится на . Далее этот столбец умножается на и складывается с i-м столбцом, при этом i = 1,…,n и i ¹ k - 1. В итоге k-я строка принимает вид соответствующей строки матрицы Фробениуса. Можно показать непосредственной проверкой, что данная процедура эквивалентна умножению матрицы B_k _-₁ справа на матрицу

Непосредственной проверкой можно убедиться, что обратной для матрицы S_k _-₁ является матрица вида:

Матрица B_k _-₁S_k _-₁ имеет k-ю строку в форме Фробениуса, однако эта матрица не подобна матрице B_k _-₁. Для обеспечения подобия надо рассмотреть произведение , которое содержит все строки с n-й по k-ю в форме Фробениуса и обеспечивает подобие.

Применяя данную процедуру последовательно ко всем строкам, кроме первой получим искомую матрицу в форме Фробениуса.

В основе метода интерполяции для построения характеристического многочлена лежит известная терема алгебры о единственности интерполяционного разложения. Для того чтобы найти коэффициенты характеристического полинома (13), необходимо задать n узловых точек a₁,a₂,…,a _n, и по ним, согласно формуле , оценить n значений характеристического полинома b₁,b₂,…,b _n. В итоге, учитывая предыдущую процедуру построения матрицы Фробениуса, можно записать следующую систему уравнений для определения коэффициентов характеристического полинома

. (14)

Узлы интерполяции можно выбирать и произвольно, но для уменьшения ошибок округления их лучше помещать между l_max и l_min, причем по возможности равномерно.

Метод интерполяции в форме (14) имеет ряд недостатков. Первый из них связан с тем, что требуется приблизительно n⁴ операций для вычисления n определителей матриц порядка n. При заметном значении n четвертая степень может привести к чрезмерно большому числу операций. Кроме того, корни интерполяционного многочлена очень чувствительны к погрешностям вычисления коэффициентов характеристического многочлена. Поскольку погрешности при вычислении коэффициентов характеристического полинома неизбежны, постольку это приводит к значительному снижению точности в оценке корней характеристического многочлена. По этой причине этим методом редко пользуются при n > 10.

На листинге_№3 приведен код программы развертывания векового определителя с помощью метода интерполяции. Кроме того, находятся корни векового уравнения, т.е. собственные значения матрицы A и сравниваются с известным ответом. В результате этого сравнения вычисляется абсолютная ошибка метода интерполяции, график которой в зависимости от порядка матрицы приведен на рис.3.

Листинг_№3

%Программа поиска собственных значений путем

%развертывания векового определителя методом

%интерполяции

%очищаем рабочее пространство

clear all

%определяем максимальный порядок матрицы

nmax=30;

%организуем цикл процедуры развертывания

%векового определителя для матриц A, у которых

%всюду нули кроме главной диагонали, где

%стоят числа 1,2,...,n

for n=1:nmax

%строим матрицу A

A=zeros(n);

for i=1:n

A(i,i)=i;

end

%определяем узлы интерполяции

for i=1:n

alpha(i)=0.3+i;

end

%определяем значения характеристического

%полинома в узлах интерполяции, т.е.

%находим beta(i)=(-1)^n*det(A-alpa(i)E)

for i=1:n

beta(i)=(-1)^n*det(A-alpha(i)*eye(n));

end

%формируем матрицу интерполяции

for i=1:n

for j=1:n

B(i,j)=alpha(i)^(n-j);

end

%формируем правую часть интерполяционной

%системы уравнений

for i=1:n

b(i)=alpha(i)^n-beta(i);

end

%находим коэффициенты векового уравнения,

%полученного методом интерполяции

p=[1;-B\b'];

%находим корни векового уравнения с помощью

%функции roots - стандартной функции MATLAB

rt=sort(roots(p));

%находим абсолютную ошибку между найденными

%корнями векового уравнения и известным

%ответом: корни есть числа 1,2,...,n

error(n)=norm(abs(rt-[1:n]'));

end

%строим график зависимости ошибки поиска

%собственных значений методом интерполяции

plot(1:nmax,error,'-*');

Из рис.3 отчетливо видно, что абсолютная ошибка в оценке собственных значений некоторой специальной матрицы путем интерполяции векового определителя довольно быстро растет и уже при n » 20 достигает 100%.

Рис.3. График зависимости ошибки вычисления собственных значений
методом интерполяции векового определителя от порядка матрицы

Помимо метода Данилевского, существуют и другие прямые методы Леверье, А.Н.Крылова, Самуэльсона и Ланцоша, которые позволяют вычислить коэффициенты векового определителя произвольной матрицы за » n³ арифметических действий, т.е. все эти методы экономичнее метода интерполяции. Однако, у всех этих методов есть наиболее существенный недостаток, найденные коэффициенты характеристического многочлена и соответственно его корни чувствительны к возможным ошибкам. Разобранный выше пример (листинг_№3) использования метода интерполяции отчетливо показал это. Поэтому реально все эти методы дают неплохие результаты в пределах порядка матрицы 10. Далее будут рассмотрены методы, которые позволяют отчасти преодолеть этот недостаток и эффективно работать с матрицами более высокого порядка.

Трехдиагональные матрицы

При использовании интерполяционного метода в предыдущем пункте нам был необходим явный вид характеристического многочлена, для того чтобы вычислить значение этого многочлена в некоторой точке l. Для трехдиагональной матрицы есть экономичный способ прямого вычислений определителя без его явного выражения в форме полинома. Это обстоятельство является важным, поскольку матрица общего вида может быть приведена преобразованием подобия к трехдиагональной форме.

Рассмотрим экономичный способ вычисления значения определителя для трехдиагональной матрицы A. Обозначим главный минор m-го порядка матрицы через . Разложим минор по элементам последней строки, которая содержит два ненулевых элемента (см. рис.4), тогда

, (15)

где — минор, дополняющий элемент матрицы . На рис.4 видно, что минор в последнем столбце содержит один ненулевой элемент , поэтому его следует разложить по элементам данного столбца. В итоге находим . Подставляя последнее представление в (15), находим рекуррентное соотношение, связывающее минор высшего порядка с минорами низшего:

, (16)

где m = 3,4,…,n.

Для расчетов по рекуррентной формуле (16) необходимо знание двух начальных значений миноров. Они легко определяются и имеют следующий вид:

. (17)

Для одного расчета значения определителя требуется приблизительно 5n арифметических операций, причем деления отсутствуют. Таким образом, для расчета значений характеристического многочлена есть быстрый и устойчивый способ расчета.

Корни многочлена можно найти методом парабол. Этот метод для многочленов не очень высокой степени (n < 50) достаточно устойчив и позволяет найти все корни, включая кратные, с приемлемой точностью. Метод парабол можно рассматривать в качестве обобщения метода секущих, где вместо прямой-секущей используется соответствующая парабола.

Рис.4. Вычисление главного минора матрицы A - l E

В качестве примера трехдиагональной матрицы рассмотрим матрицу Q, которая часто возникает при решении одномерных параболических уравнений, к которым относится, например, уравнение теплопроводности:

, (18)

где q — некоторый неотрицательный параметр. Собственные значения матрицы (18) известны и равны

, (19)

т.е. все собственные значения сосредоточены на отрезке [1,1+4q].

На листинге_№4 приведен код программы, которая выполняет две задачи: строит график характеристического многочлена и находит абсолютную ошибку отличия численных собственных значений матрицы Q от теоретических значений (19).

Листинг_№4

%Программа расчета значений векового

%определителя трехдиагональной матрицы и

%поиск корней характеристического многочлена

function tridg

global n q

%определяем размер трехдиагональной матрицы Q

n=50;

%определяем параметр матрицы Q

q=0.1;

%задаем пределы изменения собственных значений

lmin=1; lmax=1+4*q;

%определяем сетку значений аргумента lambda

%при вычислении значений характеристического

%многочлена

lambda=lmin:0.001:lmax;

for i=1:length(lambda)

%вычисляем значения векового определителя,

%согласно рекуррентным формулам (16), (17)

d(i)=determn(lambda(i));

%отыскиваем значения корней

%характеристического многочлена

root(i)=fzero(@determn,lambda(i));

end

%рисуем график зависимости значений векового

%определителя от значений параметра lambda

plot(lambda,d);

%определяем массив собственных значений,

%полученный для матрицы Q теоретически (19)

for i=1:n

rtheory(i)=1+4*q*sin((pi*i)/(2*(n+1)))^2;

end

%сортируем по возрастанию и отбрасываем

%повторяющиеся собственные значения,

%полученные численно

rt=srt(root);

nm=min(length(rtheory),length(rt));

%определяем абсолютную ошибку численной

%оценки собственных значений матрицы Q

error=norm(rtheory([1:nm])-rt([1:nm]))

%определяем функцию расчета значений

%векового определителя

function D=determn(lambda)

global n q

D1=1+2*q-lambda;

D2=(1+2*q-lambda)^2-q^2;

for m=3:n

D3=(1+2*q-lambda)*D2-q^2*D1;

D1=D2; D2=D3;

end

D=D2;

%определяем функцию сортировки и отбора

%несовпадающих корней характеристического

%многочлена

function y=srt(x)

x=sort(x);

y(1)=x(1);

k=1;

for i=1:length(x)

xi=x(i);

t=1;

for j=1:k

t=t*(abs(xi-y(j))>1e-15);

end

if t

k=k+1; y(k)=xi;

end

После запуска программы листинга_№4 генерируется график зависимости значений характеристического полинома от параметра l. Например, на рис.4 построен график полинома степени 50. Отметим, что из-за различного рода ошибок для интерполяционного метода развертывания векового определителя такие степени недоступны.

Рис.4. Изображен вековой определитель трехдиагональной
матрицы Q порядка 50

В таблице ниже приведены величины абсолютной ошибки отличий вычисленных собственных значений матрицы Q от теоретических (19).

Таблица зависимости абсолютных ошибок численной оценки собственных значений от порядка трехдиагональной матрицы Q
n	10	20	50	100	200	300
error	6.28e-016	9.42e-016	0.063	0.175	0.678	1.100

Матрица называется почти треугольной матрицей, если у нее либо ниже, либо выше трех главных диагоналей нулевые элементы. Для почти треугольных матриц также легко написать экономичный алгоритм расчета векового определителя при заданном l.

Дата добавления: 2022-01-22; просмотров: 100; Мы поможем в написании вашей работы!

Поделиться с друзьями:

12 3 Следующая ⇒

Мы поможем в написании ваших работ!