Стандартные функции интегрирования в среде MATLAB
Лекция №4
Численное интегрирование
Полиномиальная аппроксимация
Задача численного интегрирования формулируется следующим образом. Требуется найти определенный интеграл
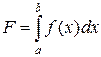 , (1)
, (1)
где функция f(x) считается непрерывной на отрезке [a,b].
В подавляющем большинстве случаев выразить интеграл через элементарные функции не удается, поэтому для приближенного вычисления интеграла функцию f(x) заменяют некоторой аппроксимирующей функцией, которая легко вычислима в рамках элементарных процедур.
Часто в качестве аппроксимирующей функции выступает полином. Для определенности выберем полином в форме Лагранжа, следуя обозначениям лекции №2, т.е.
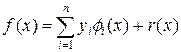 , (2)
, (2)
где yi = f(xi), i = 1,…,n, r(x) — ошибка аппроксимации Лагранжа.
Подставляя (2) в (1), получим формулу численного интегрирования или квадратурную формулу вида:
 (3)
(3)

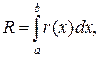
где xi, i = 1,…,n называют узлами, ci, i = 1,…,n — весами, а R — остаточным членом или погрешностью квадратурной формулы.
Согласно (3), интеграл (1) приближенно заменяется суммой, в которой узлы интегрирования и веса не зависят от интегрируемой функции.
Формула трапеций
Заменим подынтегральную функцию на отрезке [a,b] полиномом Лагранжа первой степени. Если считать в качестве узлов интегрирования концы отрезка, т.е. x1 = a, x2 = b, то полином Лагранжа L1(x) первой степени запишется в виде:
|
|
|
 (4)
(4)
 ,
, 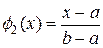 .
.
Подставляя в интеграл (1) вместо f(x) полиномом Лагранжа (4) и проводя интегрирования по x, находим
 (5)
(5)
На рис.1 приведен геометрический образ формулы интегрирования (5). Согласно рис.1, искомый интеграл, представляющий собой криволинейную трапецию, приближенно заменяется обычной, “прямой” трапецией. В этой связи формулу (5) обычно называют формулой трапеции.
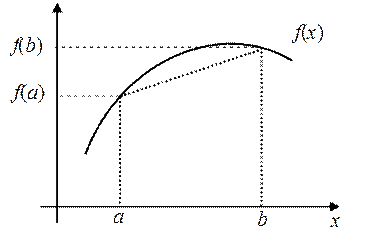
Рис.1. Геометрическая иллюстрация к формуле трапеции (5)
Найдем погрешность формулы (5). Для этого разложим подынтегральную функцию f(x) в ряд Тейлора в средней точке 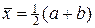 , т.е.
, т.е.
 (6)
(6)
После подстановки (6) в (5) и отбрасывания членов более высокой степени по длине отрезка интегрирования, получим
 (7)
(7)
Отметим, что в (7) не вошла первая производная 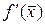 , т.к. формула трапеции является точной для линейной функции f(x). Далее в (7), разлагая
, т.к. формула трапеции является точной для линейной функции f(x). Далее в (7), разлагая 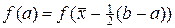 и
и  в ряд Тейлора по
в ряд Тейлора по  , получаем
, получаем
 (8)
(8)
|
|
|
Выражение (8) для оценки погрешности формулы трапеции обычно используют после того, как отрезок интегрирования заменяется сеткой с n узлами вида: a = x1 < …< xn = b и к каждому подинтервалу сетки применяют формулу трапеции, т.е.
 (9)
(9)
 ,
,
где  .
.
Формула (9) называется обобщенной формулой трапеции. На равномерной сетке обобщенная формула трапеции упрощается и может быть представлена в виде:
 (10)
(10)

где h = xi +1 - xi = const, i = 1,…,n — шаг равномерной сетки.
Оценка погрешности в (10) является асимптотической при h ® 0, т.к. отброшены члены более высокого порядка малости по степеням h. Если вторая производная подынтегральной функции не является непрерывной, а, например, кусочно-непрерывной, вместо оценки ошибки по формуле (10) остается ограничиться мажорантной оценкой:
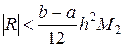 ,
,  . (11)
. (11)
Итак, согласно (10), (11), обобщенная формула трапеции имеет второй порядок точности относительно шага сетки. Для неравномерной сетки можно воспользоваться мажорантной для оценки остаточного члена, понимая под шагом 
Изучим с помощью средств MATLAB зависимость ошибки численного интегрирования по формуле трапеции от квадрата шага равномерной сетки. Определим величину test(h) =  , которая согласно (10), стремится к постоянной величине при h ® 0. Эту константу будем называть предстепенной константой. В развернутом виде функция test имеет вид:
, которая согласно (10), стремится к постоянной величине при h ® 0. Эту константу будем называть предстепенной константой. В развернутом виде функция test имеет вид:
|
|
|
test(h) =  .
.
В качестве тестируемой функции возьмем f(x)= sin(x) на отрезке [0,p], интеграл от которой на данном отрезке равен 2.
На листинге_№1 приведен код соответствующей программы. Результат работы программы содержится на рис.2.
Листинг_№1
%Программа изучения формулы трапеции
%численного интегрирования
%очищаем рабочее пространство
clear all
%определяем количество удвоений
%числа узлов сетки
nm=15;
%определяем длину начальной сетки
n=5;
%организуем цикл численных расчетов
%интеграла от sin(x) на интервале
%от 0 до pi, который, как известно,
%равен 2
for i=1:nm
h=pi/(n-1);
for j=1:n
x(j)=h*(j-1);
end
u=0;
for j=2:(n-1)
u=u+sin(x(j));
end
u=u+0.5*sin(x(1))+0.5*sin(x(end));
%находим ошибку интегрирования
%по формуле трапеции
er(i)=abs(2.0-h*u);
%удваиваем число узлов сетки
n=n*2;
end
%строим график зависимости функции test
%от шага сетки (по оси абсцисс выбираем
%логарифмическую шкалу)
for i=1:nm
hm(i)=pi/(5*2^(i-1)-1);
|
|
|
test(i)=er(i)*hm(i)^(-2);
end
plot(hm,test,'*');
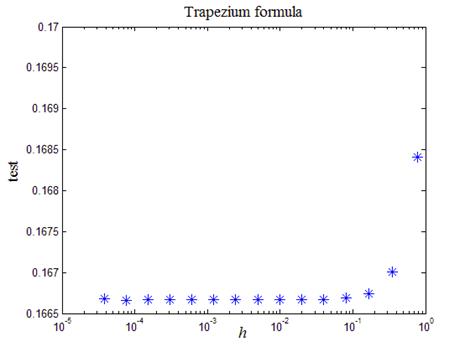
Рис.2. Зависимость предстепенной константы от шага сетки
Итоговый график на рис.2 подтверждает зависимость ошибки вычисления интеграла по формуле трапеции от квадрата шага сетки, т.к. функция test стремится к константе при h ® 0. Учитывая, что при выводе формул (9), (10) для оценки ошибки учтены лишь главные члены в разложении по степеням h, можно сделать вывод о том, что результат, представленный на рис.2 вполне удовлетворителен.
Формула Симпсона
Построим более точную формулу численного интегрирования, воспользовавшись правилами Рунге. Для этого вычислим интеграл по обобщенной формуле трапеции дважды: по исходной сетке с шагом h и по сетке с вдвое большим шагом 2h. Сетка с вдвое большим шагом получается из исходной путем выбрасывания узлов через один. Применяя правило Рунге к сетке из трех узловых точек, находим
 (12)
(12)
где  . Формула (12) называется формулой численного интегрирования Симпсона.
. Формула (12) называется формулой численного интегрирования Симпсона.
Обобщенная формула Симпсона для равномерной сетки с четным числом шагов имеет следующий вид:
 (13)
(13)
Непосредственной проверкой можно убедиться в том, что формула Симпсона точна для многочлена третьей степени. Оценку погрешности формулы Симпсона можно провести по тому же алгоритму, что и для формулы трапеции, разлагая по формуле Тейлора подынтегральную функцию для каждой пары интервалов  и
и 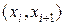 относительно узла xi. В итоге можно получить следующую оценку погрешности формулы Симпсона
относительно узла xi. В итоге можно получить следующую оценку погрешности формулы Симпсона
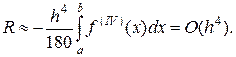 (14)
(14)
Согласно (14), обобщенная формула Симпсона (13) имеет четвертый порядок точности и дает весьма высокую точность при небольшом числе узлов интегрирования.
Как и для формулы трапеции изучим численно поведение величины test(h) = 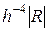 , которая есть предстепенная константа в формуле (14). Запишем функцию test(h) в развернутом виде:
, которая есть предстепенная константа в формуле (14). Запишем функцию test(h) в развернутом виде:
test(h) = 
Согласно теоретической оценке в (14), функция test(h) должна стремиться к константе при h ® 0. Воспользуемся средствами MATLAB для изучения этой зависимости на примере интегрирования функции f(x)= sin(x) на отрезке [0,p], интеграл от которой на данном отрезке равен 2.
На листинге_№2 приведен код соответствующей программы. Результат работы программы содержится на рис.3.
Листинг_№2
%Программа изучения формулы Симпсона
%численного интегрирования
%очищаем рабочее пространство
clear all
%определяем количество удвоений
%числа узлов сетки
nm=14;
%определяем длину начальной сетки
n=5;
%организуем цикл численных расчетов
%интеграла от sin(x) на интервале
%от 0 до pi, который, как известно,
%равен 2
for i=1:nm
h=pi/(n-1);
for j=1:n
x(j)=h*(j-1);
end
u1=0; u2=0;
for j=2:(n-1)
if mod(j,2)==0
u1=u1+sin(x(j));
else
u2=u2+sin(x(j));
end
end
u=sin(x(1))+4*u1+2*u2+sin(x(end));
%находим ошибку интегрирования
%по формуле Симпсона
er(i)=abs(2.0-(h/3)*u);
%удваиваем число узлов сетки
n=n*2-1;
end
%строим график зависимости функции test
%от шага сетки (по осям абсцисс и ординат
%выбираем логарифмические шкалы)
for i=1:nm
hm(i)=pi/(2^(i+1)+1);
test(i)=er(i)*hm(i)^(-4);
end
plot(hm,test,'*');
Анализ рис.3 подтверждает теоретические ожидания. Формула численного интегрирования Симпсона действительно имеет четвертый порядок точности вплоть до значений шага сетки  . В силу высокой точности метода при меньших значениях шага подходим к пределу разрядности числа типа double в MATLAB. Известно, что число типа double в MATLAB занимает 8 байт или 64 бит, что соответствует приблизительно 15 значащим цифрам в десятичной форме представления. При дальнейшем уменьшении шага точность численной оценки интеграла не улучшается, а даже ухудшается, т.к. функция test заметно растет. Таким образом, для высокоточных методов численного интегрирования процедура выбора оптимального шага сетки напрямую связана с разрядностью машинного слова, отводимого под число с плавающей запятой.
. В силу высокой точности метода при меньших значениях шага подходим к пределу разрядности числа типа double в MATLAB. Известно, что число типа double в MATLAB занимает 8 байт или 64 бит, что соответствует приблизительно 15 значащим цифрам в десятичной форме представления. При дальнейшем уменьшении шага точность численной оценки интеграла не улучшается, а даже ухудшается, т.к. функция test заметно растет. Таким образом, для высокоточных методов численного интегрирования процедура выбора оптимального шага сетки напрямую связана с разрядностью машинного слова, отводимого под число с плавающей запятой.

Рис.3. Зависимость предстепенной константы от шага сетки
Формула средних
Если на отрезке [a,b] взять единственный квадратурный узел  , то в этом случае подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. константой
, то в этом случае подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. константой  . Запишем эту квадратурную формулу в виде:
. Запишем эту квадратурную формулу в виде:
 (15)
(15)
Для оценки неизвестной величины узла интегрирования  потребуем, чтобы приближенная формула (15) была точна для линейных функций f(x) = a + b x. Это требование приводит к тому, что
потребуем, чтобы приближенная формула (15) была точна для линейных функций f(x) = a + b x. Это требование приводит к тому, что 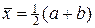 . В итоге получаем так называемую формулу средних:
. В итоге получаем так называемую формулу средних:
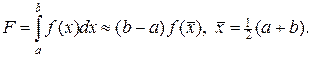 (16)
(16)
Геометрический смысл формулы (16) в том что, криволинейная трапеция приближенно заменяется прямоугольником. На рис.4 изображена данная подмена при численной оценке интеграла.
Также как и в формуле трапеции, нетрудно оценить ошибку R формулы средних:
 (17)
(17)
Разобьем интервал интегрирования на множество подинтервалов с помощью узлов сетки a = x1 <…< xn = b. К каждому из подинтервалов применим формулу (16). Оценка итоговой погрешности осуществляется с помощью формулы, аналогичной (17), т.е.
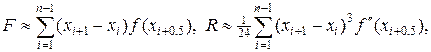 (18)
(18)
где  . Для равномерной сетки формула (18) приобретает более простой вид:
. Для равномерной сетки формула (18) приобретает более простой вид:
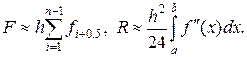 (19)
(19)
Согласно (19), формула средних имеет второй порядок точности.

Рис.4. Геометрическая интерпретация формулы средних
Ошибка в (19) формулы средних в два раза меньше ошибки (10) для формулы трапеции и имеет противоположный знак. Если сложить две численные оценки интеграла по формуле трапеции и формуле средних в комбинации 1/3 Fтрапеции + 2/3 Fсредних, h ® 2h, то получится более точный результат, соответствующий формуле Симпсона.
Как и в предыдущих двух случаях изучим численно поведение предстепенной константы формулы средних в зависимости от шага сетки.
Согласно теоретической оценке в (19) ошибка должна зависеть от величины шага во второй степени. Воспользуемся средствами MATLAB для изучения этой зависимости на примере интегрирования функции f(x)= sin(x) на отрезке [0,p], интеграл от которой на данном отрезке равен 2. Как и выше, определим предстепенную константу в виде функции test(h) = h-2|R|.
На листинге_№3 приведен код соответствующей программы. Результат работы программы содержится на рис.5.
Листинг_№3
%Программа изучения формулы средних
%численного интегрирования
%очищаем рабочее пространство
clear all
%определяем количество удвоений
%числа узлов сетки
nm=15;
%определяем длину начальной сетки
n=5;
%организуем цикл численных расчетов
%интеграла от sin(x) на интервале
%от 0 до pi, который, как известно,
%равен 2
for i=1:nm
h=pi/(n-1);
for j=1:n
x(j)=h*(j-1);
end
u=0;
for j=1:(n-1)
u=u+sin(0.5*(x(j+1)+x(j)));
end
%находим ошибку интегрирования
%по формуле средних
er(i)=abs(2.0-h*u);
%удваиваем число узлов сетки
n=n*2;
end
%строим график зависимости функции test
%от шага сетки (по оси абсцисс выбираем
%логарифмическую шкалу)
for i=1:nm
hm(i)=pi/(5*2^(i-1)-1);
test(i)=er(i)*hm(i)^(-2);
end
plot(hm,test,'*');
Из анализа графика на рис.5 следует, что функция test(h) действительно выходит асимптотически на некоторую константу при h ® 0.

Рис.5. График зависимости предстепенной константы от шага сетки
Формула Эйлера
Модифицируем остаточный член формулы трапеции (8), заменяя  на
на  . Добавляя полученную величину к формуле трапеции (5), получим формулу Эйлера (или Эйлера-Маклорена):
. Добавляя полученную величину к формуле трапеции (5), получим формулу Эйлера (или Эйлера-Маклорена):
 (20)
(20)
Стандартным методом разложения функции f(x) в ряд Тейлора можно найти остаточный член формулы Эйлера:
 (21)
(21)
Остаточный член формулы Эйлера такой же по структуре, что и остаточный член формулы Симпсона, при этом он в четыре раза его меньше.
На равномерной сетке формула Эйлера особенно просто выглядит, поскольку производные во внутренних узлах взаимно уничтожаются:
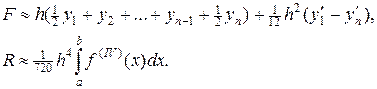 (22)
(22)
Согласно (22), формула Эйлера имеет четвертый порядок точности. Как и в предыдущих трех методах численного интегрирования, изучим предстепенную константу точности аппроксимации формулы Эйлера. Составим функцию test(h) = h-4|R|, которая, согласно теоретическим оценкам в (22), должна стремиться к некоторой константе при h ® 0. Воспользуемся средствами MATLAB для изучения этой зависимости на примере интегрирования функции f(x)= sin(x) на отрезке [0,p], интеграл от которой на данном отрезке равен 2.
На листинге_№4 приведен код соответствующей программы. Результат работы программы содержится на рис.6.
Листинг_№4
%Программа изучения формулы Эйлера
%численного интегрирования
%очищаем рабочее пространство
clear all
%определяем количество удвоений
%числа узлов сетки
nm=15;
%определяем длину начальной сетки
n=5;
%организуем цикл численных расчетов
%интеграла от sin(x) на интервале
%от 0 до pi, который, как известно,
%равен 2
for i=1:nm
h=pi/(n-1);
for j=1:n
x(j)=h*(j-1);
end
u=0;
for j=2:(n-1)
u=u+sin(x(j));
end
u=u+0.5*sin(x(1))+0.5*sin(x(end));
%находим ошибку интегрирования
%по формуле Эйлера
er(i)=abs(2.0-h*u-h^2/6);
%удваиваем число узлов сетки
n=n*2;
end
%строим график зависимости функции test
%от шага сетки (по осям абсцисс и ординат
%выбираем логарифмические шкалы)
for i=1:nm
hm(i)=pi/(5*2^(i-1)-1);
test(i)=er(i)*hm(i)^(-4);
end
plot(hm,test,'*');
Анализ рис.6 подтверждает теоретические ожидания. Формула численного интегрирования Эйлера действительно имеет четвертый порядок точности вплоть до значений шага сетки  . В силу высокой точности метода, при меньших значениях шага подходим к пределу разрядности числа типа double в MATLAB. Это выражается в том, что предстепенная константа быстро растет при дальнейшем уменьшении шага сетки.
. В силу высокой точности метода, при меньших значениях шага подходим к пределу разрядности числа типа double в MATLAB. Это выражается в том, что предстепенная константа быстро растет при дальнейшем уменьшении шага сетки.

Рис.6. График зависимости предстепенной константы от шага сетки
Процесс Эйткена
Для всех рассмотренных выше методов численного интегрирования применим метод Рунге по повышению точности расчетов, поскольку соответствующие порядки аппроксимации по степеням шага сетки известны.
Предположим, что порядок точности p существует, но неизвестен, тогда, имея в распоряжении расчеты на трех и более сетках, можно повысить точность численной оценки. Покажем это.
Выберем три сетки с постоянным отношением шага, т.е. h1 = h, h2 = qh, h3 = q2h. Пусть Fk приближенное значение интеграла на k-й сетке, тогда можно записать:
 (23)
(23)
где c = const — определенная ранее предстепенная константа.
Система трех уравнений (23) имеет три неизвестные величины: F, c, p. Решая систему уравнений (23), находим
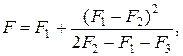

 (24)
(24)
Алгоритм численной оценки по схеме (23), (24) называют процессом Эйткена.
Рассмотрим пример сравнения друг с другом всех предыдущих методов (за исключением метода Эйлера). Применим к каждому из этих методов процесс Эйткена. В качестве примера подынтегральной функции выберем  , а интервал интегрирования [-1,1]. Интеграл от этой функции известен, он равен 4/3. Функция
, а интервал интегрирования [-1,1]. Интеграл от этой функции известен, он равен 4/3. Функция  на отрезке интегрирования имеет особенность, первая и все последующие производные являются неограниченными, поэтому априорные оценки ошибок аппроксимации неприменимы. В этой связи наиболее подходящим становится использование процесса Эйткена для уточнения численного значения интеграла.
на отрезке интегрирования имеет особенность, первая и все последующие производные являются неограниченными, поэтому априорные оценки ошибок аппроксимации неприменимы. В этой связи наиболее подходящим становится использование процесса Эйткена для уточнения численного значения интеграла.
На листинге_№5 приведен код программы, которая возвращает в командное окно MATLAB численные значения искомого интеграла для методов трапеции, Симпсона и средних, а также соответствующие их уточнения в рамках процесса Эйткена.
Листинг_№5
%Программа сравнения различных методов
%численного интегрирования друг с другом
%очищаем рабочее пространство
clear all
%определяем число узлов в начальной сетке
n=13;
%определяем цикл расчетов по трем сеткам
for i=1:3
%определяем шаг сетки
h=2.0/(n-1);
for j=1:n
x(j)=-1+h*(j-1);
end
%вычисляем интеграл по формуле трапеции
u=0;
for j=2:(n-1)
u=u+sqrt(1-abs(x(j)));
end
u=u+0.5*sqrt(1-abs(x(1)))+...
0.5*sqrt(1-abs(x(end)));
%находим ошибку интегрирования
%по формуле трапеции
trap(i)=h*u;
%вычисляем интеграл по формуле Симпсона
u1=0; u2=0;
for j=2:(n-1)
if mod(j,2)==0
u1=u1+sqrt(1-abs(x(j)));
else
u2=u2+sqrt(1-abs(x(j)));
end
end
simp(i)=(h/3)*(sqrt(1-abs(x(1)))+...
4*u1+2*u2+sqrt(1-abs(x(end))));
%вычисляем интеграл по формуле средних
u=0;
for j=1:(n-1)
u=u+sqrt(1-abs(0.5*(x(j+1)+x(j))));
end
aver(i)=h*u;
%удваиваем длину сетки
n=2*n-1;
end
%выводим на печать значения интеграла
%от функции sqrt(1-abs(x)) на отрезке [-1,1],
%который, как известно, равен 4/3
format long
trap, simp, aver
%определим поправки Эйткена к
%каждому из трех методов
Ftr=trap(1)+(trap(1)-trap(2))^2/(2*trap(2)-trap(1)-trap(3));
ptr=log((trap(3)-trap(2))/(trap(2)-trap(1)))/log(0.5);
Fsi=simp(1)+(simp(1)-simp(2))^2/(2*simp(2)-simp(1)-simp(3));
psi=log((simp(3)-simp(2))/(simp(2)-simp(1)))/log(0.5);
Fav=aver(1)+(aver(1)-aver(2))^2/(2*aver(2)-aver(1)-aver(3));
pav=log((aver(3)-aver(2))/(aver(2)-aver(1)))/log(0.5);
%выводим на печать уточненные по Эйткену значения
%интеграла для каждого из трех методов
F=[Ftr Fsi Fav]
%выводим также эффективные порядки точности
p=[ptr psi pav]
Итог работы программы листинга_№5 приведен в таблице ниже. Изучение данных в таблице приводит к следующим выводам. Все три метода дают приблизительно одну и ту же точность, несмотря на то, что для функций без особенностей метод Симпсона имеет по сравнению с методами трапеции и средних вдвое больший порядок точности. Использование процедуры Эйткена значительно повышает точность оценки интеграла во всех трех случаях, но особенно эффективно это сказалось для данных по методу Симпсона. Оценка порядка точности методов с помощью процедуры Эйткена показала, что они приблизительно одинаковы. Это и подтверждает исходный вывод о том, что все три метода приблизительно дают одну и ту же точность.
| Таблица сравнения численных методов интегрирования и | |||
| h | м. трапеции | м. Симпсона | м. средних |
| 0.16666 | 1.30735761698101 | 1.32228863372638 | 1.34046249544316 |
| 0.08333 | 1.32391005621208 | 1.32942753595577 | 1.33597352303287 |
| 0.04166 | 1.32994178962248 | 1.33195236742594 | 1.33429673194907 |
| Эйткен | 1.33339990436821 | 1.33333396174588 | 1.33329692858924 |
| p | 1.456 | 1.499 | 1.420 |
Формулы Гаусса-Кристоффеля
Перепишем исходную квадратурную формулу (3), вводя непрерывную функцию веса r(x) > 0, в следующем виде:
 (25)
(25)
где, как и выше, ci, i = 1,…,n — веса, yi = f(xi), xi, i = 1,…,n — узлы квадратурной формулы.
В рамках квадратурной формулы (25) мы можем варьировать не только значения весов, как это было в методах трапеции и Симпсона, но и положения узлов, что имело место в методе средних, где функция вычислялась в средней точке к паре соседних узлов. Таким образом, в общем случае в нашем распоряжении находится 2n свободных параметра. Если потребовать, чтобы формула (25) была точна для любого полинома степени не выше 2n - 1, то это условие может оказаться достаточным для однозначного определения всего набора весов и узлов квадратурной формулы. Если это так, то формула (25) будет называться формулой Гаусса-Кристоффеля. Изучим этот вопрос более подробно.
Считаем, что функция веса непрерывна и строго положительна на интервале (a,b), она может обращаться в нуль или в бесконечность на концах отрезка [a,b] так, чтобы существовал интеграл  . Известно[1], что при выполнении этих условий существует полная на [a,b] система ортогональных полиномов Pm(x), m = 0,1,… с заданным весом:
. Известно[1], что при выполнении этих условий существует полная на [a,b] система ортогональных полиномов Pm(x), m = 0,1,… с заданным весом:
 , (26)
, (26)
где  Все нули этих функций действительны и расположены на интервале (a,b).
Все нули этих функций действительны и расположены на интервале (a,b).
Считая узлы интегрирования известными, составим функцию
 (27)
(27)
которая в силу определения является полиномом степени не выше 2n - 1. Для функций (27) формула Гаусса-Кристоффеля точна, т.к.
 (28)
(28)
поскольку 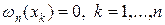 .
.
Если разложить 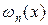 в ряд по системе ортогональных полиномов, т.е. записать представление
в ряд по системе ортогональных полиномов, т.е. записать представление  и подставить его в (28), то, согласно условиям ортогональности (26), получим bm = 0, m £ n - 1. Таким образом,
и подставить его в (28), то, согласно условиям ортогональности (26), получим bm = 0, m £ n - 1. Таким образом, 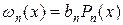 , т.е. узлами x1,…,xn формулы Гаусса-Кристоффеля являются нули полинома Pn(x).
, т.е. узлами x1,…,xn формулы Гаусса-Кристоффеля являются нули полинома Pn(x).
Зная узлы, можно легко найти веса интегрирования. Действительно функция  является полиномом степени n - 1 и для нее формула Гаусса-Кристоффеля точна. Подставляя в (25) вместо f(x) функцию f m(x), получим формулу для вычисления весов:
является полиномом степени n - 1 и для нее формула Гаусса-Кристоффеля точна. Подставляя в (25) вместо f(x) функцию f m(x), получим формулу для вычисления весов:
 (29)
(29)
Аналогично, чтобы выяснить знак веса, рассмотрим функцию 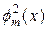 , которая является полиномом степени 2n - 2 и для нее формула Гаусса-Кристоффеля также точна. После подстановки ее в (25), получим
, которая является полиномом степени 2n - 2 и для нее формула Гаусса-Кристоффеля также точна. После подстановки ее в (25), получим
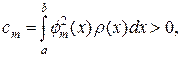
т.е. все веса положительные величины.
Подставляя в формулу Гаусса-Кристоффеля f(x) = 1, т.е. полином нулевой степени, находим интегральную оценку для совокупности весов:
 .
.
Формулы Гаусса-Кристоффеля называют еще формулами наивысшей алгебраической точности, поскольку они точны для полиномов максимальной степени 2n - 1.
Рассмотрим частные случаи.
1.Формулы Гаусса-Кристоффеля становятся просто формулами Гаусса при r(x) = 1. При r(x) = 1 ортогональными полиномами называются полиномы Лежандра, которые в справочниках[2] обычно приводятся, исходя из отрезка интегрирования [-1,1]. Ниже приведены несколько первых полиномов:

Если xk и ck, k = 1,…,n узлы и веса формул Гаусса на отрезке [-1,1], то переход к произвольному отрезку [a,b] осуществляется преобразованием:
 .
.
Ниже в таблице приведены несколько первых значений узлов и весов квадратурных формул Гаусса.
| Значения узлов и весов квадратурных | ||
| n = 1 | x1 = 0 | c1 = 2 |
| n = 2 | 
| c1 = c2 = 1 |
| n = 3 |  , x2 = 0 , x2 = 0
| c1 = c3 = 5/9, c2 = 8/9 |
Следуя таблице можно выписать следующие три квадратурные формулы Гаусса на отрезке [-1,1].
 (30)
(30)
 (31)
(31)
 (32)
(32)
Выражение (30) есть обычная формула средних записанная для отрезка [-1,1]. Две другие формулы (31) и (32) ранее еще не приводились.
Приведем без вывода погрешность аппроксимации R для общих формул Гаусса:
 (33)
(33)
Квадратурные формулы (30) — (32) преобразуем к произвольному отрезку [a,b], введем равномерную сетку a = x1 <…< xn = b и к каждому из подинтервалов применим формулы Гаусса (30) — (32), тогда
 (30¢)
(30¢)
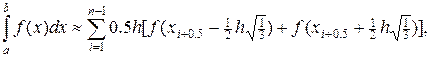 (31¢)
(31¢)
 (32¢)
(32¢)
где  , h = xi+1 - xi = const, i = 1,…,n. Согласно (33), квадратурные формулы (30¢) — (32¢) имеют порядки точности h2, h4 и h6 соответственно. Проверим это.
, h = xi+1 - xi = const, i = 1,…,n. Согласно (33), квадратурные формулы (30¢) — (32¢) имеют порядки точности h2, h4 и h6 соответственно. Проверим это.
На листинге_№6 приведен код соответствующей программы по вычислению предстепенных констант ошибок аппроксимации каждой из формул, т.е. вычисляются функции test(h) = h-2k|R|, k = 1,2,3. На рис.7 приведен итог работы кода программы.
Листинг_№6
%Программа изучения формул Гаусса
%численного интегрирования
%очищаем рабочее пространство
clear all
%определяем количество удвоений
%числа узлов сетки
nm=15;
%определяем длину начальной сетки
n=5;
%организуем цикл численных расчетов
%интеграла от sin(x) на интервале
%от 0 до pi, который, как известно,
%равен 2
for i=1:nm
h=pi/(n-1);
for j=1:n
x(j)=h*(j-1);
end
%производим вычисления по
%формуле средних
u=0;
for j=1:(n-1)
u=u+sin(0.5*(x(j+1)+x(j)));
end
%находим ошибку интегрирования
%по формуле средних
er1(i)=abs(2.0-h*u);
%производим вычисления по
%второй формуле Гаусса (31')
u=0; u1=1.0/(2*sqrt(3.0));
for j=1:(n-1)
u=u+sin(0.5*(x(j+1)+x(j))-u1*h)+...
sin(0.5*(x(j+1)+x(j))+u1*h);
end
%находим ошибку интегрирования
%по второй формуле Гаусса (31')
er2(i)=abs(2.0-0.5*h*u);
%производим вычисления по
%третьей формуле Гаусса (32')
u=0;
u1=0.5*sqrt(3.0/5); u2=5.0/9; u3=8.0/9;
for j=1:(n-1)
u=u+u2*sin(0.5*(x(j+1)+x(j))-u1*h)+...
u3*sin(0.5*(x(j+1)+x(j)))+...
u2*sin(0.5*(x(j+1)+x(j))+u1*h);
end
%находим ошибку интегрирования
%в третьей формуле Гаусса (32')
er3(i)=abs(2.0-0.5*h*u);
%удваиваем число узлов сетки
n=n*2;
end
%строим график зависимости функции test
%от шага сетки (по осям абсцисс и
%ординат выбираем логарифмические шкалы)
for i=1:nm
hm(i)=pi/(5*2^(i-1)-1);
test1(i)=er1(i)*hm(i)^(-2);
test2(i)=er2(i)*hm(i)^(-4);
test3(i)=er3(i)*hm(i)^(-6);
end
plot(hm,test1,'*',hm,test2,'p',hm,test3,'h');
На рис.7 приведены три графика расчета зависимости предстепенных констант от шага сетки для трех квадратурных формул Гаусса (30¢) — (32¢). Из анализа графиков на рис.7 видно, для первой квадратурной формулы средних предстепенная константа остается таковой во всем счетном диапазоне шагов сетки, для второй квадратурной формулы предстепенная константа начинает резко возрастать, когда шаг сетки становится меньшим величины  и, наконец, для третьей квадратурной формулы предстепенная константа начинает расти, когда шаг сетки становится меньшим величины
и, наконец, для третьей квадратурной формулы предстепенная константа начинает расти, когда шаг сетки становится меньшим величины  . В силу высокой точности второй и третьей формул Гаусса поведение предстепенных констант можно объяснить тем, что оба метода “чувствуют” ограниченность мантиссы представления чисел типа double на MATLAB.
. В силу высокой точности второй и третьей формул Гаусса поведение предстепенных констант можно объяснить тем, что оба метода “чувствуют” ограниченность мантиссы представления чисел типа double на MATLAB.

Рис.7. Поведение предстепенных констант трех формул Гаусса
(30¢) — (32¢) в зависимости от шага сетки
Формулы Гаусса (30¢) — (32¢) являются довольно экзотичными, поскольку они требуют, во-первых, знания вида функции для вычисления ее значений в довольно неожиданных точках, во-вторых, для достижения высокой точности требуется высокая гладкость функции.
2.Формулы Эрмита следуют из квадратурных формул на отрезке [-1,1], взятых с весовой функций вида:  . При этих условиях ортогональны полиномы Чебышева первого рода Tn(x), n =0,1,… Для них узлы и веса интегрирования следующие:
. При этих условиях ортогональны полиномы Чебышева первого рода Tn(x), n =0,1,… Для них узлы и веса интегрирования следующие:

3.Формулы Гаусса-Кристоффеля позволяют производить расчеты на полупрямой [0,+¥) с весовой функцией 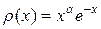 . При этих условиях ортогональными будут полиномы Лагерра
. При этих условиях ортогональными будут полиномы Лагерра  . Если же область интегрирования вся прямая (-¥,+¥), то для весовой функции
. Если же область интегрирования вся прямая (-¥,+¥), то для весовой функции  ортогональными будут полиномы Эрмита.
ортогональными будут полиномы Эрмита.
Стандартные функции интегрирования в среде MATLAB
В среде MATLAB для интегрирования методом трапеции используется функция trapz, для интегрирования методом Симпсона — функция quad, для интегрирования методом Гаусса — функция quadl.
Пример обращения к функции trapz приведен на листинге_№7. В качестве результата будет возвращено число, близкое к 2 — точному значению интеграла от sin(x) на отрезке [0,p].
Листинг_№7
%Найдем с помощью функции trapz
%определенный интеграл от sin(x)
%на отрезке [0,pi]
%очищаем рабочее пространство
clear all
%задаем вектор узлов квадратурной
%формулы трапеции, считая их
%случайными величинами из
%отрезка [0,pi]
x=sort(rand(1,101)*pi);
%вычисляем значения функции в узлах
y=sin(x);
%находим и выводим значение интеграла,
%точное значение которого 2
trapz(x,y)
Алгоритм приближенного вычисления интеграла с помощью метода Симпсона на базе функции quad включает процедуру рекурсии с последующим возможным делением отрезка интегрирования пополам. Разность значений интеграла между текущей и предыдущей рекурсиями сравниваются и, если результат сравнения превышает задаваемый порог точности, процедура повторяется.
Пример обращения к функции quad приведен на листинге_№8. В качестве результата будет возвращено число, близкое к 2 — точному значению интеграла от sin(x) на отрезке [0,p].
Листинг_№8
%Найдем с помощью функции quad
%определенный интеграл от sin(x)
%на отрезке [0,pi]
%очищаем рабочее пространство
clear all
%задаем точность вычисления интеграла
tol=1e-3;
%находим и выводим значение интеграла,
%точное значение которого 2
format long
quad('sin(x)',0,pi,tol)
При оценке интеграла с помощью функции quadl используются квадратурные формулы Гаусса, причем более высокого порядка, чем это было рассмотрено нами выше. Отметим, что для четырех узлов квадратурная формула Гаусса называется формулой Лобатто, а для семи узлов — формулой Кронрода. Функция quadl находит приближенные значения интеграла по Лобатто и Кронроду, сравнивает их. Если разница между ними превышает заданную погрешность, отрезок интегрирования разбивается на 6 неравных частей, рекурсивная процедура оценки интеграла применяется для каждой из частей и результаты складываются. Во всем остальном обращение к функции quadl аналогично обращению к функции quad.
Наконец, проиллюстрируем возможность аналитического вычисления определенных интегралов в среде MATLAB. Для этого возьмем несколько примеров определенных интегралов из сборника задач и упражнений по математическому анализу[3]:
 (33)
(33)
Программа для взятия интегралов (33) приведена на листинге_№9.
Листинг_№9
%Программа аналитического вычисления
%нескольких определенных интегралов
%очищаем рабочее пространство
clear all
%интеграл 1)
int1=int('x*(2-x^2)^12',0,1)
%интеграл 2)
int2=int('x/(x^2+x+1)',-1,1)
%интеграл 3)
int3=int('1/(x*sqrt(x^2-1))',-2,-1)
%интеграл 4)
int4=int('x^15*sqrt(1+3*x^8)',0,1)
%интеграл 5)
int5=int('sin(x)*sin(2*x)*sin(3*x)',0,pi/2)
%интеграл 6)
int6=int('(x*sin(x))^2',0,pi)
В таблице приведены значения шести определенных в (33) интегралов, взятых пакетом MATLAB.
| Значения 6 интегралов, определенных в (33) и | |||||
| 1) | 2) | 3) | 4) | 5) | 6) |
| 8191/26 | 1/2*log(3)-1/6*3^(1/2)*pi | -1/3*pi | 29/270 | 1/6 | 1/6*pi^3-1/4*pi |
Разобранные примеры аналитического взятия интегралов означают, что соответствующая процедура MATLAB может заменить собой некоторые справочники. Помимо аналитического задания подынтегральной функции в MATLAB допустимо также определять ее в виде отдельной функции или отдельного файла.
[1] Никифоров А.Ф., Уваров В.Б. Основы теории специальных функций. — М.: Наука, 1974.
[2] См., например, приложение “Ортогональные многочлены” к книге: Калиткин Н.Н. Численные методы. — М.: Наука, Гл. ред. физ.-мат. лит., 1978. с.501.
[3] Демидович Б.П. Сборник задач и упражнений по математическому анализу. — М.: Наука, 1972, с.195.
Дата добавления: 2022-01-22; просмотров: 58; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
