Среднеквадратическое приближение

⇐ ПредыдущаяСтр 2 из 2

Часто значения интерполируемой функции y₁, y₂,…, y_n определяются из эксперимента с некоторыми ошибками, поэтому пользоваться точным приближением в узлах интерполяции неразумно. В этом случае более естественно приближать функцию не по точкам, а в среднем, т.е. в одной из норм L_p.

Пространство L_p — множество функций g(x), определенных на отрезке [a,b] и интегрируемых по модулю с p-ой степенью, если определена норма

(15)

Сходимость в такой норме называется сходимостью в среднем. Пространство L₂ называется гильбертовым, а сходимость в нем — среднеквадратичной.

Пусть заданы функция f(x) и множество функций f(x) из некоторого линейного нормированного пространства. В контексте проблемы интерполирования, аппроксимации и приближения можно сформулировать следующие две задачи.

Первая задача это аппроксимация с заданной точностью, т.е. по заданному e найти такую f(x), чтобы выполнялось неравенство ||f(x) - f(x)|| £ e.

Вторая задача это поиск наилучшего приближения, т.е. поиск такой функции f _*(x), которая удовлетворяет соотношению:

||f(x) - f _*(x)|| = inf||f(x) - f(x)|| = e.

Определим без доказательства достаточное условие существования наилучшего приближения. Для этого в линейном пространстве функций выберем множество, параметризованное выражением

(16)

где набор функций f₁(x),…,f_n(x) будем считать линейно независимым.

Можно показать[2], что в любом нормированном пространстве при линейной аппроксимации (16) наилучшее приближение существует, хотя не во всяком линейном пространстве оно единственно.

Рассмотрим гильбертово пространство L₂(r) действительных функций, интегрируемых с квадратом с весом r(x) > 0 на [a,b]. Норма в этом пространстве равна 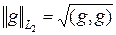, где скалярное произведение (g,h) определено по формуле:

Подставляя в условие наилучшего приближения линейную комбинацию (16), находим

Приравнивая к нулю производные по коэффициентам a_k, k = 1,…,n, получим систему линейных уравнений

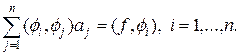(17)

Определитель системы уравнений (17) называется определителем Грама. Определитель Грама отличен от нуля, поскольку считается, что система функций f₁(x),…,f _n(x) линейно независима.

Таким образом, наилучшее приближение существует и единственно. Для его получения необходимо решить систему уравнений (17). Если система функций f₁(x),…,f _n(x) ортогонализирована, т.е. (f _i,f _j) = d _ij, где d _ii = 0, d _ij = 0, i¹j, i,j = 1,…,n, то система уравнений может быть решена в виде:

, (f _i,f _j) = d _ij. (18)

Найденные согласно (18) коэффициенты a₁,…,a_n называются коэффициентами обобщенного ряда Фурье.

Если набор функций f₁(x),…,f _n(x),… образует полную систему, то в силу равенства Парсеваля 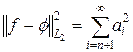при n ® ¥ норма погрешности неограниченно убывает. Это означает, что наилучшее приближение среднеквадратично сходится к f(x) с любой заданной точностью

Отметим, что поиск коэффициентов наилучшего приближения с помощью решения системы уравнений (17) практически нереализуем, поскольку с ростом порядка матрицы Грама ее определитель быстро стремится к нулю и матрица становится плохо обусловленной. Решение системы линейных уравнений с такой матрицей приведет к значительной потере точности. Проверим это.

Пусть в качестве системы функций f _i, i = 1,…,n выбираются степени, т.е. f _i = xⁱ ^-1, i = 1,…,n, тогда, полагая в качестве отрезка аппроксимации отрезок [0,1], находим матрицу Грама

(f _i,f _j) = 1/(i + j - 1), i,j = 1,…n. (19)

Матрица Грама вида (19) называют еще матрицей Гильберта. Это классический пример так называемой плохо обусловленной матрицы.

С помощью MATLAB рассчитаем определитель матрицы Гильберта в форме (19) для некоторых первых значений n. На листинге_№5 приведен код соответствующей программы.

Листинг_№5

%Вычисление определителя матриц Гильберта

%очищаем рабочую область

clear all;

%выберем максимальное значение порядка

%матрицы Гильберта

nmax=6;

%строим цикл для формирования матриц

%Гильберта и вычисления их определителей

for n=1:nmax

d(n)=det(hilb(n));

end

%выводим значения определителей

%матриц Гильберта

format short e

После отработки кода листинга_№5, в командном окне MATLAB должны появиться значения детерминантов матриц Гильберта для первых шести матриц. В таблице ниже приведены соответствующие численные значения порядков матриц (n) и их определителей (d). Из таблицы отчетливо видно сколь быстро определитель матрицы Гильберта стремится к нулю при росте порядка и, уже начиная с порядков 5, 6, становится неприемлемо малым.

Таблица значений определителя матриц Гильберта

n	1	2	3	4	5	6
d	1.00e+000	8.33e-002	4.62e-004	1.65e-007	3.74e-012	5.36e-018

Численная ортогонализация системы функций f _i, i = 1,…,n также приводит к заметной потере точности, поэтому, чтобы учитывать большое число членов в разложении (16), необходимо либо проводить ортогонализацию аналитически, т.е. точно, либо пользоваться уже готовой системой ортогональных функций.

Если при интерполяции обычно используют в качестве системы базисных функций степени, то при аппроксимации в среднем в качестве базисных функций выбирают многочлены, ортогональные с заданным весом. Наиболее употребительными из них являются многочлены Якоби, частным случаев которых являются многочлены Лежандра и Чебышева. Используют также полиномы Лагерра и Эрмита. Более подробно об этих полиномах можно ознакомиться, например, в приложение ортогональные полиномы книги².

Метод наименьших квадратов

Пусть вещественная функция y = f(x) задана таблично в точках x₁,…,x_N своими значениями y_i = f(x_i), i = 1,…,N, тогда скалярное произведение можно определить по формуле:

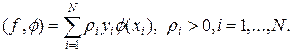(20)

С учетом (20) условие наилучшего среднеквадратичного приближения приобретет следующий вид:

(21)

Подставим в (21) представление для аппроксимирующей функции в виде (16) с числом членов n £ N. Далее можно следовать стандартно, приравнивая к нулю производные по коэффициентам a₁,…a_n, получаем уравнения для поиска этих коэффициентов, которые, в свою очередь, могут быть решены обычным образом. Данный способ нахождения аппроксимирующей функции называется методом наименьших квадратов.

Метод наименьших квадратов широко используется для обработки экспериментальных данных, в которых значения некоторых функций измерены с заметной погрешностью. В этом случае вес r _i, i = 1,…n связывают с точностью данных, т.е., чем выше точность отдельного значения, тем выше вес и, наоборот. В итоге аппроксимирующая кривая будет проходить ближе к более точным значениям измеряемой функции. При n » N среднеквадратическая аппроксимация близка к интерполяции, при n заметно меньше N аппроксимирующая кривая будет заметным образом сглаживать данные.

С помощью MATLAB освоим процедуру метода наименьших квадратов. На листинге_№6 приведен соответствующий код программы, который строит полином степени n-1, обеспечивающий наилучшее среднеквадратическое приближение аппроксимируемой функции, заданной набором точек на плоскости (x₁,y₁),…,(x_N,y_N).

Листинг_№6

%Метод наименьших квадратов

%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%очищаем рабочую область

clear all;

%определяем число точек N

N=11;

%определяем множество аргументов

%аппроксимируемой функции в виде

%равномерной сетки

for i=1:N

x(i)=(i-1.0)/(N-1);

end

%моделируем значения аппроксимируемой

%функции с помощью датчика случайных

%чисел, распределенных по нормальному

%закону со средним 0 и ст. откл. 1

y=[];

for i=1:length(x)

y=[y randn];

end

%веса скалярного произведения (20)

%выберем равными единице

ro=ones(size(x));

%определим число неизвестных

%коэффициентов n представления (16)

n=3;

%строим методом наименьших квадратов,

%аппроксимирующий полином степени n-1

sp=spap2(1,n,x,y,ro);

%рисуем аппроксимирующий полином на

%фоне значений аппроксимируемой функции

fnplt(sp);

hold on;

plot(x,y,'*');

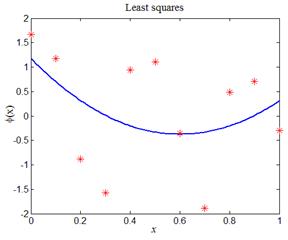
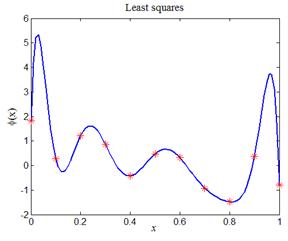
При работе с кодом листинга_6 необходимо запустить программу и убедиться, что с ростом числа аппроксимирующих коэффициентов n от 1 до N, сглаживание данных при малых n заменяется интерполяцией при n » N. На рис.6,а приведен первый случай, а на рис.6,б — второй.


Рис.6,а. Аппроксимирующая кривая — парабола (n = 3, N = 11)	Рис.6,,. Аппроксимирующая кривая — полином степени 10 (n = 11, N = 11)

Построим теперь наилучшее среднеквадратическое приближение с помощью сплайна. На листинге_№7 приведен соответствующий код программы MATLAB, который генерирует график с дискретным набором аппроксимируемой функции и сплайном того или иного порядка.

Листинг_№7

%Метод наименьших квадратов при

%аппроксимации функции с помощью сплайна

%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%очищаем рабочую область

clear all;

%задаем область аппроксимации

a=0.0; b=1.0;

%определяем множество аргументов

%аппроксимируемой функции

x=a:0.1:b;

%моделируем значения аппроксимируемой

%функции с помощью датчика случайных

%чисел, распределенных по нормальному

%закону со средним 0 и ст. откл. 1

y=[];

for i=1:length(x)

y=[y randn];

end

%веса скалярного произведения (20)

%выберем равными единице

ro=ones(size(x));

%определим порядок сплайна

%n=4 - кубический сплайн

n=1;

%задаем узлы стыковки соседних сплайнов

xk=[0.25 0.5];

%строим методом наименьших квадратов,

%аппроксимирующий сплайн

sp=spap2(augknt([a b xk],n),n,x,y,ro);

%рисуем аппроксимирующий полином на

%фоне значений аппроксимируемой функции

fnplt(sp);

hold on;

plot(x,y,'*');

На рис.7 приведены различные варианты работы кода программы листига_№7. На рис.7,а приведена аппроксимация искомой функции тремя сплайнами первого порядка (n = 1, полиномы нулевой степени), на рис.7,б — второго порядка (n =2, полиномы первой степени), на рис.7,в,г — третьего и четвертого порядков (n = 3, 4, полиномы второй и третьей степени) соответственно.

Многомерная интерполяция

С многомерной интерполяцией познакомимся на примере восполнения функции z = f(x,y) двух независимых аргументов x, y. Пусть аппроксимируемая функция z задана в узлах прямоугольной сетки (x_i,y_j), i = 1,…,n, j = 1,…,m, т.е. известны z_ij = f(x_i,y_j), i = 1,…,n, j = 1,…,m и требуется найти z = f(x,y). На прямоугольной сетке удобна так называемая последовательная интерполяция. Сначала проведем интерполяцию Лагранжа по переменной x при фиксированном значении y_j, затем проведем интерполяцию Лагранжа по y при фиксированном значении x_i. В итоге можно построить следующее выражение для интерполирующей функции, аналогичное одномерной интерполяционной формуле (7):

(22)

Согласно (22), для случая, когда n = m = 1 находим P_1,1(x,y) = z₁₁, т.е аппроксимация полиномами нулевой степени сводится к отождествлению значения функции в аппроксимируемой точке (x,y) ближайшим известным значением z_ij.


Рис.7,а. Сплайн первого порядка	Рис.7,б. Сплайн второго порядка

Рис.7,в. Сплайн третьего порядка	Рис.7,г. Сплайн четвертого порядка

Рассмотрим еще один частный случай формулы (22), когда n = m = 2, тогда

(23)

Формула интерполяции (23) называют еще линейной или билинейной, она осуществляет аппроксимацию поверхности фрагментом гиперболического параболоида — седла.

Оба частных случай двумерной интерполяции при n = m = 1,2 проиллюстрируем средствами MATLAB на примере визуализации потенциала сил кулоновского взаимодействия четырех одинаковых зарядов. На листинге №8 приведен соответствующий код.

Листинг_№8

%Программа визуализации потенциала

%кулоновских сил при взаимодействии

%четырех одинаковых зарядов

%очищаем рабочую область

clear all;

%задаем пределы изменений по переменным x и y

xl=-2.0; xr=2.0;

yl=-2.0; yr=2.0;

%формируем сетку в которой задана

%аппроксимируемая функция

x=xl:0.2:xr;

y=yl:0.2:yr;

[X,Y]=meshgrid(x,y);

%задаем степень кулоновского взаимодействия

lamda=1.0;

%вычисляем потенциал в узлах сетки

for i=1:length(x)

for j=1:length(y)

Z(i,j)=...

((x(i)-1)^2+(y(j)-1)^2+0.001)^(-lamda/2)+...

((x(i)+1)^2+(y(j)-1)^2+0.001)^(-lamda/2)+...

((x(i)+1)^2+(y(j)+1)^2+0.001)^(-lamda/2)+...

((x(i)-1)^2+(y(j)+1)^2+0.001)^(-lamda/2);

end

%выбираем метод интерполяции

method='nearest';

%строим двемерный график по имеющимся

%значениям аппроксимируемой функции

surf(X,Y,Z);

hold on;

%определяем сетку, в узлах которой определим

%интерполирующую функцию

xi=xl:0.05:xr;

yi=yl:0.05:yr;

[XI,YI]=meshgrid(xi,yi);

%возвращаем значения интерполяционного

%полинома в узлах сетки

ZI=interp2(X,Y,Z,XI,YI,method);

%строим двумерный график по значением

%интерполяционного многочлена

surf(XI,YI,ZI+60);

Предлагается запустить программу листинга_№8 и визуализировать искомый потенциал для четырех способов интерполяции:

· method='nearest' — аппроксимация полиномами степени 0 (площадками, случай n = m = 1 по нашей классификации);

· method='linear' — аппроксимация кусочными билинейными полиномами первой степени согласно (23), случай n = m = 2;

· method='cubic' — бикубическая интерполяция;

· method='spline' — интерполяция кубическим сплайном.

Последние два способа интерполяции нами не обсуждались, но мы используем их для сравнения с первыми двумя.

На рис.8 приведен итог двумерной интерполяции согласно коду программы листинга_№8. На каждом из рисунков приведено по два двумерных графика. Нижний — грубый график — исходные данные об аппроксимируемой функции, верхний — двумерный график, построенный по интерполяционному выражению в соответствии с одним из четырех методов.


Рис.8,а. Аппроксимация полиномами степени 0	Рис.8,б. Аппроксимация полиномами степени 1 — билинейная интерполяция

Рис.8,в. Аппроксимация полиномами степени 3	Рис.8,г. Аппроксимация кубическим сплайном

При изучении рис.8 отчетливо видно повышение качества изображения двумерной поверхности при переходе от довольно грубого метода аппроксимации с помощью полинома нулевой степени (рис.8,а) к менее грубой — билинейной аппроксимации (рис.8,б) и далее уже к вполне удовлетворительным способам аппроксимации с помощью кубического полинома и сплайна (рис.8,в,г).

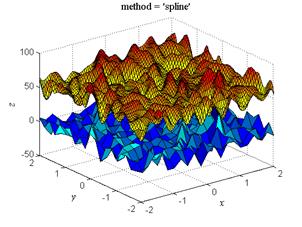
Наконец, для сравнения на рис.9 приведена визуализация всех четырех режимов аппроксимации для случайного двумерного поля, распределенного по нормальному закону со средним 0 и стандартным отклонением 10.


Рис.9,а. Аппроксимация полиномами степени 0	Рис.9,б. Аппроксимация полиномами степени 1 — билинейная интерполяция

Рис.9,в. Аппроксимация полиномами степени 3	Рис.9,г. Аппроксимация кубическим сплайном

[1] Самарский А.А., Гулин А.В. Численные методы: Учеб. пособие для вузов. — М.: Наука, Гл. ред. физ.-мат. лит., 1989, с.144.

[2] Калиткин Н.Н. Численные методы.. — М.: Наука, Гл. ред. физ.-мат. лит., 1978, с.53.

Дата добавления: 2022-01-22; просмотров: 43; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!