Проверка гипотезы о линейности

⇐ ПредыдущаяСтр 2 из 2

Если r²_ху и R²_ху равны, или их разность меньше, чем 0,1, то нет смысла усложнять работу и можно использовать линейную функцию.

Оценку надежности проводят с помощью критерия Стьюдента

Если t_ф > t_табл, то различие R²и r² существенны и замена функции на линейную невозможна.

Пример: По 7 территориям Уральского региона известны следующие данные

№	Расх. на покупку продовол. т-ров,%	Ср.днев.з/п 1 раб.,руб.	У = lg y	Х = lg х	У ∙Х	Х^2	Ух	у - Ух	(у-Ух)^2	х∙у	(х - хср.)^2
1	68,8	45,1	1,8376	1,6542	3,0397	2,7363	61	7,8	60,8	3102,9	96,0
2	61,2	59	1,7868	1,7709	3,1641	3,1359	56,3	4,9	24,0	3610,8	16,8
3	59,9	57,2	1,7774	1,7574	3,1236	3,0884	56,8	3,1	9,6	3426,3	5,3
4	56,7	61,8	1,7536	1,7910	3,1406	3,2076	55,5	1,2	1,4	3504,1	47,6
5	55	58,8	1,7404	1,7694	3,0794	3,1307	56,3	-1,3	1,7	3234,0	15,2
6	54,3	47,2	1,7348	1,6739	2,9040	2,8021	60,2	-5,9	34,8	2563,0	59,3
7	49,3	55,2	1,6928	1,7419	2,9488	3,0344	57,4	-8,1	65,6	2721,4	0,1
	405,2	384,3	12,3234	12,1587	21,4002	21,1354	403,5	1,7	198,0	22162,3	240,3

Задание: 1) построить степенную функцию, рассчитать её параметры;

2) оценить с помощью критерия Фишера надежность модели и проверить гипотезу о линейности;

3) рассчитать коэффициенты эластичности; проверить гипотезу о линейности.

Степенная модель имеет вид: у = а ∙ х^в

lgy= lga + b ∙ lgx

У = lgy; A = lga; X = lgx

У = A + bx

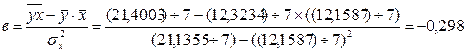
У = 2,278 – 0,298 ∙ х

у = 10^2,278 ∙ х^-0,298 = 189,7 ∙ х^-0,298

Рассчитаем критерий Фишера:

Доля объясненной дисперсии составляет 14%.

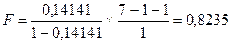
F_табл = 6,61

F_факт <F_табл => с вероятностью 95% уравнение статистически не значимо. Это означает, что а и b получены случайным образом, и по такому уравнению нельзя делать прогноз.

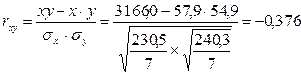
Тема 8. Множественная регрессия

Спецификация модели

Парная регрессия дает хороший результат, если выявлен Олин фактор, очень сильно влияющий на результат, а влиянием всех остальных факторов можно пренебречь.

Такие зависимости характерны для химических, физических и биологических исследований, когда существует возможность постановки эксперимента.

Поставить эксперимент – организовать среду, когда все остальные факторы, кроме одного, будут зафиксированы на одном уровне.

В экономике такие зависимости встречаются редко, и отсутствует возможность проведения эксперимента. Поэтому для экономики характерны многофакторные зависимости.

Спецификация модели заключается в решении двух вопросов:

1) отбор факторов из множества существующих у = f (х₁, х₂, …, х_n)

у = f (x_i, x_i₊₁, …, x_k), где k < n

2) выбор вида уравнения регрессии

Отбор факторов при построении уравнения множественной регрессии

Факторы должны удовлетворять условиям:

1. Они должны быть количественно измеримы.

Если факторы качественные, нужно придать им количественную оценку ( например, проранжировать, присвоить рейтинг, т.п.).

2. Факторы не должны быть взаимозависимыми (интеркоррелированными), т.е. факторы не должны быть в функциональной связи между собой.

Если факторы интеркоррелированны, то невозможно определить их индивидуальное влияние на результат. Т.о. параметры уравнения невозможно интерпретировать.

3. Факторы должны объяснять корреляцию независимой переменной (результат), т.е. каждый следующий фактор, включенный в модель, должен увеличивать r².

Т.е. при включении дополнительного фактора r² должно возрастать существенно.

Существенно – если изменяется первый или второй знак после запятой.

R²_n = 0,852

R²_n₊₁ = 0,903 (нужно включить)

R²_n₊₂ = 0,904 (несущественное изменение) (не нужно включать)

Если в модели есть «лишние» факторы, то модель может стать статистически не значимой.

Т.о. отбор факторов проводится в два этапа:

1) подбирают факторы исходя из существенности проблемы;

2) отбирают факторы по какому-нибудь алгоритму.

Тема 9. Мультиколлинеарность

Считают, что факторы коллинеарны, если r_xixj ≥ 0,7, т.е факторы х_i и x_j тесно связаны между собой и находятся в линейной зависимости => х_i и x_j друг друга дублируют и один из них рекомендуется исключить из регрессии.

Оставляют в уравнении фактор, имеющий: 1) тесную связь с результатом;

2) наименьшую тесноту связи с другими факторами.

Для оценки мультиколлинеарности нужно построить матрицу парных линейных коэффициентов корреляции:

MS Excel: Сервис → Анализ данных → Корреляция → Выбор диапазона

В результате выходит таблица

	у	х₁	х₂	х₃
у	1
х₁	0,8	1
х₂	0,7	0,8	1
х₃	0,6	0,5	0,2	1

R_x₁_x₂ = 0,8 > 0,7 => х₁ и x₂ коллинеарны.

у = f (х₂, х₃) фактор х₃наиболее независим в данной системе, т.к. его линейные коэффициенты корреляции наименьшие (0,2).

Существуют случаи, когда нужно включить в модель факторы, имеющие сильную связь между собой, тогда используют следующие подходы для преодоления сильной межфакторной корреляции:

1. Исключение факторов;

2. Преобразование факторов, чтобы уменьшить корреляцию между ними:

А) переход к первым разностям

х₁; х₂; х₃

х₂ → х₂ - х₁; х₃ → х₃ – х₂ и т.д.

Каждый уровень ряда заменяем на абсолютный прирост, соответствующий этому уровню. Используется в рядах динамики.

Б) метод главных компонент

Переход от исходных переменных к их линейным комбинациям.

3. Совмещенное уравнение регрессии

Отражает не только зависимость результата от фактора, но и совместное влияние факторов на результат.

у = f (х₁, х₂, х₃)

у_х = а+в₁х₁+в₂х₂+в₃х₃+в₁₂х₁∙х₂+ в₁₃х₁∙х₃+ в₂₃х₂∙х₃+в₁₂₃ х₁∙х₂∙х₃

Ограничения для каждого параметра при х – нужно 6-7 измерений. Для данного уравнения нужно 42-49 измерений, что не всегда доступно.

4. Переход к уравнениям приведенной формы

Выражаем фактор из другого уравнения и подставляем в исходное уравнение.

Тема 10. Выбор формы уравнения регрессии

1) Линейная функция y = a + b₁x₁ + b₂x₂ + b₃x₃ + … + b_nx_n

«+»: - сравнительно просто отыскать параметры уравнения;

- сравнительно просто интерпретировать.

Результат увеличивается на величину b₁ при изменении фактора х₁ на единицу и всех остальных факторов, зафиксированных на среднем уровне.

2) Степенная функция y = a ∙ x₁^b¹ ∙ x₂^b² ∙ … ∙ x_n^bn

Интерпретация: b1, b2, bn - коэффициенты эластичности. Показывают, на сколько изменился результат в среднем при изменении соответствующего фактора на 1 %.

Другие функции используются редко.

Тема 11. Оценка параметров уравнения множественной регрессии

Отыскание параметров уравнения

Параметры уравнения множественной регрессии оцениваются МНК.

Для отыскания параметров сроится система нормальных уравнений.

y = a + b₁x₁ + b₂x₂ + b₃x₃ + … + b_nx_n

Тогда система нормальных уравнений принимает следующий вид:

∑y = na + b₁∑x₁ + b₂∑x₂ + b₃∑x₃ + … + b_n∑x_n

∑y ∙ x₁ = a∑x₁ + b₁∑x₁² + b₂∑x₁∙ x₂ + b₃∑ x₁∙x₃ + … + b_n∑ x₁∙x_n

∑y ∙ x₂ = a∑x₂ + b₁∑x₁∙ x₂ + b₂∑x₂² + b₃∑ x₂∙x₃ + … + b_n∑ x₂∙x_n

…

∑y ∙ x_n = a∑x_n + b₁∑x₁∙ x_n + b₂∑x₂∙ x_n + b₃∑ x₂∙x₃ + … + b_n∑x_n²

Эту систему можно записать в следующем виде:

А = (a; b₁; b₂; b_n)

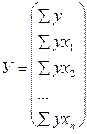
Х = А ∙ У А = У ∙ Х^-1

Если функция степенная, или другая нелинейная, то её сначала линеализуют, а затем применяют МНК.

Тема 12. Частные уравнения регрессии

Есть линейное уравнение вида y = a + b₁x₁ + b₂x₂ + b₃x₃ + … + b_nx_n, то можно найти частное уравнение регрессии вида

Эти уравнения регрессии показывают связь между результатом и соответствующим фактором при закреплении других слагаемых на среднем уровне, т.е. позволяют точно оценить влияние фактора на результат.

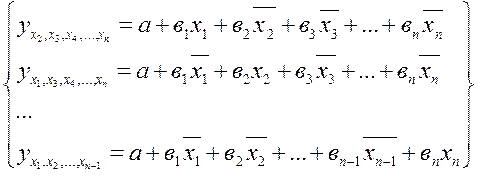
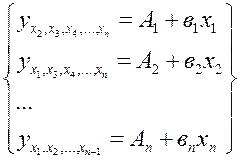
Эти уравнения позволяют определить частные коэффициенты эластичности, которые показывают, на сколько процентов изменился результат под воздействием одного фактора изолированно в процентах.

Коэффициенты эластичности определяются точно также как для уравнения парной линейной регрессии:

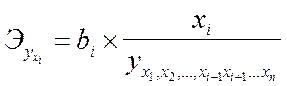
Тема 13. Множественная корреляция

После отыскания параметров уравнение множественной регрессии нужно проверить на статистическую значимость и надежность.

Для этого используются: 1) Индекс множественной корреляции

2) Частные коэффициенты корреляции

3) F – критерий Фишера

4) t – статистика

1) Индекс множественной корреляции R

σ²_у – общая дисперсия результативного признака;

σ²_ост – остаточная дисперсия для уравнения.

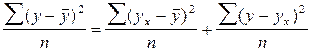
Этот индекс показывает, на сколько тесная связь между факторами и результатом.

Если модель построена правильно, то индекс множественной корреляции существенно отличается от максимального индекса парной корреляции.

R_x₁_x_2…_xn > max (r_xy)

Индекс линейной корреляции может служить индикатором необходимости включения в модель дополнительного признака.

Если при включении дополнительного признака изменяется второй знак, то включение этого признака оправдано.

R²_{х1,х2,…,х}_n показывает процент объясненной регрессии с помощью данного уравнения.

2) Частные коэффициенты корреляции – это коэффициенты линейной корреляции, характеризующие тесноту связи между результатом и соответствующим фактором при устранении влияния всех других факторов, входящих в уравнение.

R² в числителе = R² всего уравнения

R² в знаменателе = коэффициент детерминации при исключении фактора Х_i

Порядок расчета: 1. Составляется матрица парных коэффициентов корреляции;

2. Находятся частные коэффициенты корреляции первого порядка (частные коэффициенты корреляции между У и двумя другими факторами).

х₁ и х₂: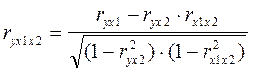

х₁, х₂, х₃: r_yx₁_x₂ r_yx₂_x₃r_yx₁_x₃

Далее проводим анализ, включение какого фактора оказывает сильное влияние на результат.

3) Критерий Фишера

Д_фактор – факторная сумма квадратов, деленная на одну степень свободы.

Д_ост – остаточная сумма квадратов, деленная на одну степень свободы.

k – количество факторов или независимых переменных.

Коэффициент Фишера показывает значимость уравнения регрессии.

Если F_факт > F_табл – то уравнение регрессии статистически значимо.

4) t – статистика рассчитывается стандартным образом, и показывает статистическую значимость того или иного параметра.

Тема 14. Фиктивные переменные во множественной регрессии

Задача: Включить в модель качественный признак.

y = f (х₁; х₂)

y – частота потребления кофе;

х₁ – личный доход;

х₂ – пол.

х₂ – переменная качественная, её нужно заменить на количественную. Для этого введем фиктивную переменную z.

Количество фиктивных переменных z должно соответствовать количеству значений, принимаемых признаком.

х₂ → z:

Составим уравнение: у = a + b₁x₁ + c₁z₁ + c₂z₂ + ε и решаем его стандартным способом (МНК).

Интерпретация уравнения регрессии: коэффициент при х₁ имеет стандартную интерпретацию, коэффициенты при z₁и z₂ нужны для составления частных уравнений регрессии.

В данном случае интерпретации подлежат частные коэффициенты корреляции.

Разность между коэффициентами при фиктивных переменных показывает относительное влияние качественного признака.

Дата добавления: 2022-01-22; просмотров: 29; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!