Лекция 11. Полиномиальные коды.

Принцип построения полиномиальных кодов.

При полиномиальном кодировании каждое сообщение отождествляется с многочленом, а само кодирование состоит в умножении на фиксированный многочлен. Полиномиальные коды блочные и отличаются от рассмотренных ранее только алгоритмами кодирования идекодирования.

Пусть а= а₀…а _m _-1 двоичное сообщение. Тогда сопоставим ему многочлен a (х) = a ₀ + a ₁ x + … + a_m _-1 x^m ^-1. Все вычисления происходят в поле классов вычетов по модулю 2, т. е. от результата любой арифметической операции берется остаток от его деления на 2.

Например, последовательности 10011 при т =5 соответствуем многочлен 1 +х³ +х⁴.

Зафиксируем некоторый многочлен степени к,

Полиномиальный код с кодирующим многочленом g (х) кодирует слово сообщения а(х) многочленом b (х) = a (х) b (х) = b ₀ + b ₁ х +…+ b_n _-1 xⁿ ^-1 или кодовым словом из коэффициентов этого многочлена b = b ₀ … b_n _-1 . Условия g₀≠ 0 и g_k ≠ 0 необходимы, потому что в противном случке b ₀ и b_n _-1 не будут нести никакой информации, т.к. они всегда будут нулями.

Пример. Рассмотрим кодирующий многочлен g (х)= 1 + x ² +х³. Сообщение 01011, отвечающее многочлену а(х) = х + х³ + x ⁴, будет закодировано коэффициентами многочлена b (х) = g ( x ) a ( x ) = x + x ⁵ + х¹. т.е. b= 01000101.

Полиномиальный код с кодирующим многочленом g (х) степени k является матричным кодом с кодирующей матрицей G размерности т (т + k ):

Т.е. ненулевые элементы в j-й строке это последовательность коэффициентов кодирующего многочлена, расположенных с j-гo по (j +к)-й столбцах.

Например, (3, 6)-код с кодирующим многочленом 1 +х+х³ отвечает матрице

Полиномиальные коды являются групповыми.

Это следует из того, что коды, получаемые матричным кодированием, -групповые.

Рассмотрим (т, п)-код с кодирующим многочленом g(х). Строка ошибок е = е₀… e_n _-1 останется необнаруженной в том и только в том случае, если соответствующий ей многочлен е(х) = е₀ + e ₁ x + …+ e_n _-1 xⁿ ^-1 делится на g(х).

Действительно, a(х) g (х) + е(х ) делится на g(х) тогда и только тогда, когда e(x ) делится на g(х). Поэтому любая ошибка, многочлен которой не делится на g(х), будет обнаружена и, соответственно, любая ошибка, многочлен которой делится на g(х), не может быть обнаружена.

Таким образом, обнаружение ошибки при использовании полиномиального кода с кодирующим многочленом g(х) может быть реализовано при помощи алгоритма деления многочленов к остатком: если остаток ненулевой, то при передаче произошло искажение данных.

Коды Хэмминга можно строить как полиномиальные, например, кодирующий многочлен x ³ + х² + 1 определяет совершенный (4, 7)-код, отличный от рассмотренного ранее.

Вообще же, если кодирующий многочлен g(х), порождающий соответствующий ( m , n )-код, не является делителем ни одного из многочленов вида x^j + 1 при j <0, то минимальное расстояние между кодовыми словами порожденного им кода не меньше 3.

Пусть d - минимальное расстояние между кодовыми словами, оно равно минимуму среди весов ненулевых кодовых слов. Предположим d = 2. Тогда существует a ( x ) такой, что a (х) g (х) = b (х) и степень b (х) не больше n . Вес b равен 2, поэтому b ( x ) = х ^m + x^l и l < т < п. Следовательно, b(х) = x^l ( x^m ^- ^l + 1), что означает, что x^m ^- ^l + 1 должен делиться на g(х), а это невозможно по условию. Если предположить, что d =1, то это приведет к утверждению о том, что х^т должен делиться на g(х), что тоже противоречит условию. Итак, d ≥ 3.

Кодирующий многочлен x ¹¹ + x ⁹ + х⁷ + x ⁶ + х⁵ + х + 1 определяет совершенный (12, 23)-код Голея (Golay) с минимальным расстоянием между кодовыми словами 7.

В 1971 году финскими и советскими математиками было доказано, что кроме кодов Хэмминга и Голея других совершенных кодов нет.

Наиболее интересными среди полиномиальных кодов являются циклические коды, в которых вместе с любым кодовым словом вида b ₀ ... b _п-2 b_n _-1 есть кодовое слово b_n _-1 b ₀ ... b_n _-2 .

Линейные коды.

Двоичные коды строятся с использованием только двух элементов. В литературе встречаются различные условные обозначения символов двоичного кода. Наиболее употребительные из них рекомендованы МСЭ-Т.

При реализации кодов необходимо представлять их символы в виде элементов дискретного сигнала той или иной формы, удобной для выполнения последующих операций и передачи по линиям связи.

Формы сигналов не обязательно жестко закрепляются за символами кода. Широко распространены правила относительного кодирования, когда один символ кода отображается чередованием форм, а второй - формой предыдущего элемента. Выбор формы сигнала самым непосредственным образом определяет: энергетический спектр (занимаемую полосу частот), возможности выделения сигналов синхронизации, скорость передачи в расчете на единицу полосы частот (удельную скорость передачи).

Формы цифровых сигналов, предназначенных для передачи по линии связи, получили наименование линейных кодов (ЛК). ЛК применяются для передачи данных без модуляции в первичной полосе частот, начинающейся с нуля. Иначе говоря, кадры цифровых систем передачи, сформированные в соответствии с правилами ПЦИ или СЦИ и представляющие собой обычные двоичные последовательности, перед подачей в линию связи подвергаются соответствующему преобразованию в линейном кодере.

Циклические коды.

Циклические коды являются частным случаем линейных и представляют собой наиболее разработанную часть последних. Основным их достоинством является простота технической реализации, благодаря чему они и обратили на себя внимание специалистов. Ценным свойством таких кодов является способность обнаруживать не только одиночные ошибки, но и пакеты ошибок. Пакетом ошибок длиной L называют число разрядов сообщения, искаженных подряд.

Свое название циклические коды получили из-за следующего свойства: если комбинация

аn-1аn-2 ... ala0

относится к коду, то комбинация, полученная путем циклического сдвига элементов, т.е. комбинация

аn-2 ... ala0 an-1,

также относится к коду. Направление сдвига не имеет значения. Один сдвиг в одном направлении эквивалентен п-1 сдвигам в другом направлении.

Математической основой построения циклических кодов является представление кодовых комбинаций в виде многочленов от некоторой переменной х с коэффициентами, равными элементам кодовых комбинаций, и операцией по mod2. Кодовая комбинация

представляется многочленом

Пример:

Многочлен кодовой комбинации 01001 имеет вид

При построении и исследовании циклических кодов приходится производить сложение, умножение и деление многочленов. Они выполняются обычным образом, надо учитывать только особенности самих операций:

При сложении многочленов складываются коэффициенты при одинаковых степенях х;

Произведение многочленов есть сумма попарных произведений всех членов сомножителей;

Деление многочленов производят по частям, последовательно освобождаясь от старшей степени еще не поделенной части многочлена.

Кодовый полином циклический код строится с помощью так называемого порождающего многочлена g(x) степени г.

Признаком принадлежности n-разрядной комбинации данному коду является делимость соответствующего ей многочлена на порождающий. Если многочлен принятой комбинации делится на порождающий, то считается, что она совпадает с посланной. Если деление происходит с остатком, то принятая комбинация к коду не относится, т.е. произошло наложение ошибки. Вид остатка при достаточной избыточности позволяет указать место ошибки.

Способы образования кодового многочлена:

1.Кодовые комбинации циклического кода можно образовать путем умножения информационных многочленов, соответствующих информационным элементам, на порождающий многочлен. Недостатком такого способа является изменение информационных элементов.

Пример:

Информационным элементам 1111 соответствует информационный многочлен

Пусть порождающий многочлен

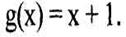
Произведение

что соответствует кодовой комбинации 10001, в которой исходные информационные элементы не сохранены. Для исключения этого недостатка используют следующий прием.

2. Информационный многочлен Р(х) умножается на хг, где г - старшая степень образующего многочлена g(x), и полученное выражение делится на g(x). В результате получится частное Q(x) и остаток R(x) степени меньше г:

xrP(x) = g(x)Q(x) + R(x).

Перенесем R(x) в левую часть:

xrP(x) + R(x) = g(x)Q(x).

Правая часть последнего равенства кратна g(x) и, следовательно, является кодовым многочленом F(x), т.е.

xrP(x) + R(x) = F(x).

Именно так получаются кодовые многочлены. Первое слагаемое кодового многочлена имеет нулевые коэффициенты в г младших членах. Этот многочлен соответствует сдвинутой влево на г разрядов информационной части Р(х). Степень многочлена R(x) меньше г, поэтому его коэффициенты не изменяют нулевые коэффициенты первого многочлена при их сложении. Таким образом, информационные элементы в кодовой комбинации сохраняются, а проверочными элементами являются коэффициенты остатка R(x), число которых равно степени порождающего многочлена.

Пример:

Определить кодовую комбинацию при информационной части 101011 и порождающем многочлене

g(x) = x2 + x+l.

Очевидно,

Р(х) = х5 + хЗ+х + 1,

F(x) = х7 + х5 + хЗ + х2 + х+1,

чему соответствует кодовая комбинация 10101111. Шесть первых элементов информационные, остальные два - проверочные, соответствующие остатку

R(x) = x+1.

Свойства циклических кодов:

Минимальное кодовое расстояние d циклического кода не превышает числа членов порождающего многочлена.

Циклический код с порождающим многочленом степени г>1 обнаруживает любую одиночную и любую двойную ошибку, т.е. имеет d>3.

Код с порождающим многочленом х + 1 является кодом с четным числом единиц.

Циклический код с порождающим многочленом g(x)(x+l) имеет d>4.

Код с порождающим многочленом g(x) степени г обнаруживает все пакеты ошибок длины г или меньше

Дата добавления: 2022-01-22; просмотров: 32; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 9 10 11 12 13 141516 17 18 Следующая ⇒

Мы поможем в написании ваших работ!