Глава 2. Системы линейных алгебраических уравнений
Раздел 1. Линейная и векторная алгебры
Глава 1. Матрицы
Матрицей А называется таблица чисел. Если матрица состоит из m строк и n столбцов, то говорят, что размерность матрицы есть m на n. Количество элементов в такой матрице равно произведению mn. Обозначение матрицы
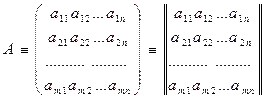 (1.1)
(1.1)
или сокращенно A=(aij)m n. Числа aij, составляющие матрицу, называются ее элементами. Первый индекс указывает номер строки, второй - номер столбца.
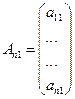
Матрица называется прямоугольной, если mn, Если m=n, то матрица называется квадратной и число n - порядком матрицы. Матрица, содержащая один столбец, называется матрица-столбец. Матрица, состоящая из одной строки - матрица-строка. У таких матриц элементы могут иметь только один номер.
 ;
;  (1.2)
(1.2)
Матрица, все элементы которой равны нулю, называется нулевой матрицей.
Для квадратной матрицы порядка n (число строк равно числу столбцов и равно n) A=(аij)n,n, элементы a11, a22, ..., ann с одинаковыми индексами образуют главную диагональ. Элементы a1 n, a2 n-1, ..., an 1 образуют побочную диагональ. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали, равны нулю: aij=0 при ij. Диагональная матрица обозначается так
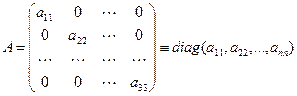 . (1.3)
. (1.3)
Диагональная матрица, у которой все диагональные элементы равны, единице называется единичной и обозначается
|
|
|
 (1.4)
(1.4)
Квадратная матрица называется треугольной, если все элементы, стоящие ниже (или выше) главной диагонали, равны нулю:
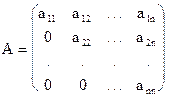 , . (1.5)
, . (1.5)
Каждой квадратной матрице ставится в соответствие число, называемое детерминантом или определителем, который обозначается символами detA или D(A) или |aij|.
Для матрицы 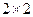 определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
определитель находится по формуле: произведение элементов главной диагонали минус произведение элементов побочной диагонали
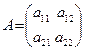 det(A) =
det(A) =  = a11 a22 – a12 a21. (1.6)
= a11 a22 – a12 a21. (1.6)
Для матрицы  определитель находится по формуле
определитель находится по формуле
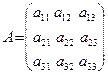 det(A) =
det(A) = 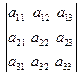 = a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
= a11 a22 a33 + a12 a23 a31 + a13 a21a32 - a13a22 a31 –
- a12 a21 a33 - a11a23 a32. (1.7)
Пример. Вычислить определитель матрицы  .
.
Решение:
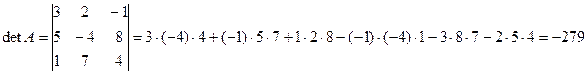
Определитель единичной матрицы равен единице det I = 1.
Минором Mik называется определитель меньшего порядка (размера), полученный при вычеркивании i-той строки и k-того столбца.
|
|
|
Алгебраическим дополнением Aik называется минор, знак которого определяется по правилу Aik = (-1)i+k Mik.
Определитель можно представить в виде суммы произведений элементов любой строки или столбца на их алгебраические дополнения, например
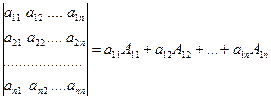 , (1.8)
, (1.8)
где
 ,
, 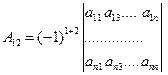 ,…….
,…….  .
.
Квадратная матрица называется невырожденной (неособенной), если det A¹0, и вырожденной (особенной), если det A=0. Определитель треугольной матрицы равен произведению диагональных элементов:
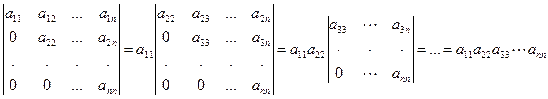 . (1.9)
. (1.9)
Действия над матрицами
Равенство матриц. Две матрицы A=(aij)m,n и B=(bij)k,q называются равными, если они одинаковы по размеру (m=k, n=q) и их соответствующие элементы равны (aij = bij).
Сложение матриц. Складывать можно лишь матрицы одинакового размера. Суммой двух матриц A=(aij)m,n и B=(bij)m,n называется матрица C=(cij)m,n того же размера, причем элементы матрицы C равны сумме соответствующих элементов матриц A и B, т.е.
C = A+B, если cij = aij + bij. (1.10)
|
|
|
Пример.
 .
.
Умножение матрицы на число. Произведением матрицы A=(aik)m,n на число a называется матрица C=(cij)m,n, элементы которой получаются из соответствующих элементов матрицы A умножением на число a:
C = a A, где cij = a×aij. (1.11)
Пример.
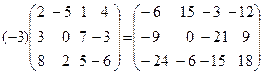 .
.
Операции сложения матриц и умножения число называются линейными операциями. Эти операции обладают следующими свойствами:
A + B = B + A (перестановочный закон);
(A + B) + C = A + (B + C) (сочетательный закон);
(a+b)A=aA+bA (распределительный закон);
(A + B) = A + B;
A + (-A) = 0
A + 0 = A,
где A, B, C, 0 матрицы одного размера, a, b - числа.
Замечание. Пусть A, B - квадратные матрицы порядка n > 1. Линейные операции над матрицами не переносятся на их определители, т.е. det(A+B) ¹ detA + detB, det(aּA) ¹ aּdetA, но det(aA)=an ּdetA.
Произведение матриц. Произведение матриц AmkּBkn = Ckn определено только в том случае, если число столбцов матрицы A равно числу строк матрицы B, при этом матрица С имеет размер mּn. Элементы матрицы С определяются по формуле
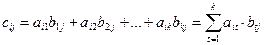 (1.12)
(1.12)
Умножение матриц производится по правилу "строка на столбец".
|
|
|
Произведение матриц не перестановочно, в общем случае AּB BּA.
Пример. Найти произведения матриц A = 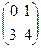 и B =
и B =  .
.
Поскольку это квадратные матрицы одного размера, то умножение таких матриц возможно, причем существует и АВ и ВА. В соответствии с (2.2) имеем:
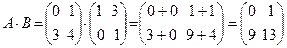
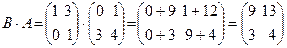
Свойства операции умножение матриц:
1) Aּ (BּC) = (AּB) ּС;
2) aּ (AּB) = (aּA) ּB = Aּ (aּB);
3) (A+B) ּC = AּC + BּC;
4) Cּ (A+B) = CּA + CּB,
где a - число, A, B, C матрицы, для которых произведения cуществуют;
5) если A, B - квадратные матрицы одного порядка, то
det (AּB) = detA ּ detB.
Транспонирование матриц. Рассмотрим произвольную матрицу
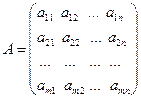 .
.
Матрица  полученная из матрицы A заменой строк столбцами, называется транспонированной по отношению к A.
полученная из матрицы A заменой строк столбцами, называется транспонированной по отношению к A.
Например, если A = 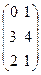 , то At =
, то At = 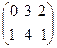 .
.
Свойства операции транспонирования матриц
1) (At)t = A;
2) (A + B)t= At+ Bt;
3) (aּA)t= aAt:
4) (AּB)t = BtּAt,
(AּB)t = BtּAt, где A и B - матрицы, a- число;
5) Если A- квадратная матрица, то detA=detAt.
Глава 2. Системы линейных алгебраических уравнений
Пусть дано n неизвестных x1, x2, xi, … , xn. Система m линейных уравнений с n неизвестными xi, 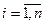 , имеет вид
, имеет вид
 (2.1)
(2.1)
здесь аij коэффициенты при неизвестных, причем i – номер уравнения, а j – номер неизвестного. Величины bi - свободные члены. В в матричной форме систему можно записать так
AּX = B, (2.2)
где 
Матрица A, составленная из коэффициентов при неизвестных, называется основной (базовой) матрицей системы, X - матрица-столбец неизвестных, B - матрица-столбец свободных членов. Если к основной матрице системы приписать столбец свободных членов, то получится расширенная матрица системы уравнений
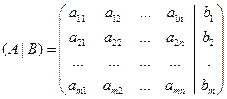 (2.3)
(2.3)
Если все свободные члены равны нулю, то система называется однородной, в противном случае система неоднородна. Линейные системы, полученные одна из другой путем элементарных преобразований (перестановкой двух уравнений, умножением одного из них на число, не равное нулю, почленным сложением двух уравнения) называются эквивалентными (или равносильными). Все эквивалентные системы имеют одинаковые решения.
Решение системы линейных алгебраических уравнений с помощью формул Крамера и методом Гаусса.
Рассмотрим систему n линейных алгебраических уравнений с n неизвестными:
|
| ||||
| Вычислим определитель системы
| ||||
 (2.5) (2.5)
| ||||
Если  ¹0, то система (2.4) имеет решение, и при том единственное. Если
¹0, то система (2.4) имеет решение, и при том единственное. Если  = 0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
= 0, то система (1) либо не имеет решений, либо имеет бесчисленное множество решений.
В дальнейшем мы будем предполагать, что  ¹0.
¹0.
1. Решение с помощью формул Крамера.
Если определитель системы  ¹0, то, согласно формулам Крамера, решение системы (2.4) можно представить в виде
¹0, то, согласно формулам Крамера, решение системы (2.4) можно представить в виде
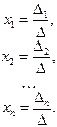 (2.6) (2.6)
|
Здесь
|
| 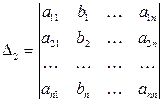 ; ;
| ||
|
| |||
Определитель 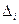 (i=1, 2,…, n) отличается от определителя системы
(i=1, 2,…, n) отличается от определителя системы 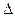 тем, что
тем, что 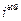 столбец
столбец 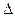 заменен столбцом из свободных членов, т.е. столбец
заменен столбцом из свободных членов, т.е. столбец 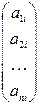 заменен на столбец
заменен на столбец  .
.
Пример. Дана расширенная матрица системы  . Решить систему методом Крамера.
. Решить систему методом Крамера.
Решение. Запишем систему в стандартной форме
 .
.
Определитель данной системы
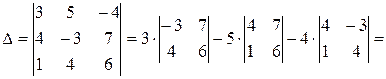

Вычислим определители 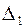 ,
, 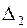 и
и  :
:

 .
.
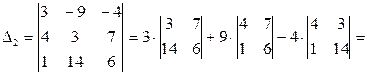
 .
.

 .
.
Решение системы: 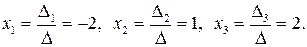
Для того чтобы убедиться в правильности решения, подставим эти значения  в исходную систему
в исходную систему
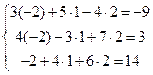 .
.
2. Решение методом Гаусса. Пусть есть система (2.4) с определителем 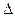 ¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
¹0. Нашей системе можно сопоставить расширенную матрицу, в которой содержится вся информация о системе
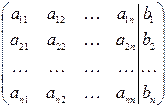 . .
|
Метод Гаусса состоит в том, что система (2.4) с помощью ряда элементарных преобразований сводится к новой системе, расширенная матрица которой имеет вид
 . (2.7) . (2.7)
|
Т.е. в результате преобразований все коэффициенты матрицы  становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:
становятся равными нулю, кроме диагональных элементов, которые становятся равными единице:  при
при  и
и 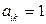 при
при  . Столбец свободных членов
. Столбец свободных членов 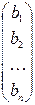 превращается в новый столбец
превращается в новый столбец  .
.
Если мы привели нашу матрицу к диагональному виду, то решение системы записывается очень просто:
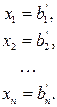 (2.8) (2.8)
|
Таким образом, решение системы сводится к совершению элементарных преобразований, в результате которых расширенная матрица (5) превращается в расширенную матрицу (6).
К элементарным преобразованиям системы (1) относятся следующие:
1) перемена местами уравнений (т.е. перемена местами строк расширенной матрицы);
2) умножение или деление любого уравнения системы (1) на число, отличное от 0 (т.е. умножение или деление строки расширенной матрицы на число, отличное от 0);
3) изменение любого уравнения системы (1) путем прибавления к нему другого уравнения системы, умноженного на число, отличное от 0 (т.е. изменение строки расширенной матрицы путем прибавления к ней другой строки, умноженной на число, отличное от 0).
Пример. Найти решение системы методом Гаусса.
 .
.
Решение. Определитель системы 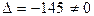 . Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
. Таким образом, система имеет единственное решение. Найдем его методом Гаусса. Начальная расширенная матрица имеет вид
 .
.
Далее мы будем приводить нашу матрицу к диагональному виду и выписывать ее вид после каждого шага преобразований.
1-й шаг. Разделим 1-ю строку матрицы на 2.
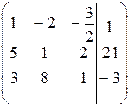 .
.
2-й шаг. 1-ю строку оставляем без изменения. Вместо 2-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-5), складываем ее со 2-й строкой, тогда новые числа, стоящие во 2-й строке расширенной матрицы, будут следующие:


Вместо 3-й строки записываем следующую ее комбинацию с 1-й: 1-ю строку умножаем на (-3) и складываем ее с 3-й строкой, тогда
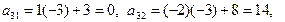
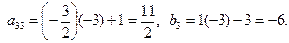
Расширенная матрица примет вид
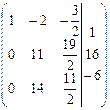 .
.
В результате первых 2-х шагов 1-й столбец  преобразовался в
преобразовался в 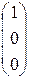 .
.
3-й шаг. Делим вторую строку на 11.
 .
.
4-й шаг. 2-ю строку оставляем без изменения. Вместо 1-й строки записываем следующую ее комбинацию со 2-й: 2-ю строку умножаем на 2 и складываем ее с 1-й строкой, тогда

Вместо 3-й строки записываем ее комбинацию со 2-й: 2-ю строку умножаем на (-14) и складываем ее с 3-й строкой, тогда
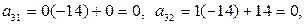
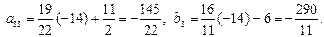
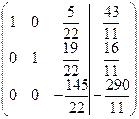 .
.
В результате 3-го и 4-го шагов 1-й столбец матрицы не изменился, а 2-й превратился в  .
.
5-й шаг. Делим 3-ю строку на 
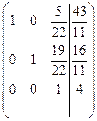 .
.
6-й шаг. 3-ю строку оставляем без изменения. Вместо 1-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на  и складываем ее с 1-й строкой, тогда
и складываем ее с 1-й строкой, тогда
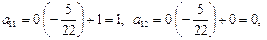
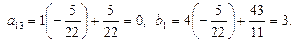
Вместо 2-й строки записываем ее комбинацию с 3-й: 3-ю строку умножаем на 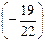 и складываем ее со 2-й строкой, тогда
и складываем ее со 2-й строкой, тогда
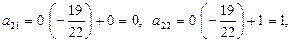

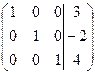 .
.
В результате 5-го и 6-го шагов 3-й столбец принял вид  .
.
Таким образом, решение системы следующее: 
Проверка
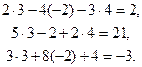
Таким образом, смысл метода Гаусса состоит в том, что сначала 1-й столбец исходной матрицы приводим к виду  , затем 2-й - к виду
, затем 2-й - к виду  и, наконец, 3-й – к виду
и, наконец, 3-й – к виду  . При этом происходит преобразование столбца свободных членов.
. При этом происходит преобразование столбца свободных членов.
Глава 3. Векторная алгебра
Вектором называется направленный отрезок прямой. Из определения следует, что вектор имеет три характеристики: прямую на которой он лежит, направление по прямой и длину. Первые две характеристики объединяются одним понятием – направление. Обозначаются вектора по точкам начала и конца АВ или  . Различают три вида векторов: свободные вектора, которые не меняются при параллельном переносе, вектора, которые можно переносить только по прямой на которой они лежат (например, вектора сил в механике) и радиус вектора, начало которых всегда находится в начале координат. Мы будем рассматривать только свободные вектора. Свободные вектора называют равными, если они лежат на одной или параллельных прямых, направлены в одну сторону и имеют одинаковую длину (рис 3.1), т. е. параллельный перенос вектора не меняет. Свободные вектора обозначают одной буквой
. Различают три вида векторов: свободные вектора, которые не меняются при параллельном переносе, вектора, которые можно переносить только по прямой на которой они лежат (например, вектора сил в механике) и радиус вектора, начало которых всегда находится в начале координат. Мы будем рассматривать только свободные вектора. Свободные вектора называют равными, если они лежат на одной или параллельных прямых, направлены в одну сторону и имеют одинаковую длину (рис 3.1), т. е. параллельный перенос вектора не меняет. Свободные вектора обозначают одной буквой  или а, b и т. д. Длину вектора обозначают при помощи модульных скобок
или а, b и т. д. Длину вектора обозначают при помощи модульных скобок  = ç а ç= а.
= ç а ç= а.
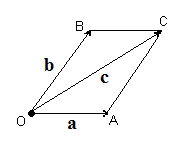
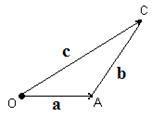
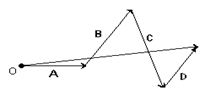
Вектора складывают по правилу параллелограмма: совмещают концы векторов, строят на векторах как на сторонах параллелограмм; суммой векторов называют вектор диагонали исходящий их общего начала a + b = c (рис.3.2). Вектора можно складывать и по правилу треугольника (рис. 3.3). Правило треугольника можно применить к сумме любого числа векторов (рис 3.4)

| |||
| |||
Умножение вектора на число λ идет по следующему правилу: при умножении на положительное число направление вектора сохраняется, при умножении на отрицательное – меняется на противоположное, а длина определяется по правилу (рис 3.5).
çλ а ç =  а (3.2)
а (3.2)
По определению a - b = a + (-1)b.

|
| ||||
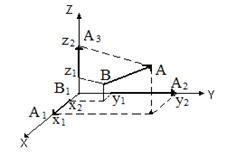
Проекцией вектора на ось ОХ называется число равное разности координат проекций конца и начала вектора
prOXAB = x2 – x 1= çAB çcos(α), (3.6)
где α - угол между вектором и осью (рис. 3.6).
Аналогично можно ввести проекцию вектора на оси OY и OZ:
prOYAB = y2 – y1= çABçcos(β) (3.6)
и
prOZAB = z2 – z1= çABçcos(γ) , (3.7)
где β и γ углы между вектором АВ и осями OY и OZ. Косинусы углов cos(α), cos(β) и cos(γ) называют направляющими косинусами
cos2(α)+cos2(β)+cos2(γ) = 1. (3.8)


|
Если ввести i, j и k - единичные вектора осей ОХ, OY и OZ (их называют ортами), то вектор
A1B1 = i(x2 – x1), A2B2 = j(y2 – y1) и A3B3 = k(z2 – z1). (3.9)
По правилу сложения векторов (рис. 3.7):
AB = A1 B1 + A2 B2 + A3 B3 = i(x2 – x1) + j(y2 – y1) + k(z2 – z1) ≡{(x2 – x1), (y2 – y1), (z2 – z1)}.
Равенство
AB = {(x2 – x1), (y2 – y1), (z2 – z1)} (3.10)
называется «запись вектора в форме проекций».
Операции с векторами a, b заданными в форме проекций идут по следующему правилу:
a = {x1, y1, z1)}; b = {x2, y2, z2}
a + b ={ (x1+x2), (y1 + y2), (z1 + z2)}; (3.11)
λa = {λx1, λ y1, λz1}. (3.12)
Скалярным произведением векторов a = {x1, y1, z1)}; b = {x2, y2, z2} называют число равное произведению длин векторов на косинус угла между ними
а × b = (a,b) = ça ç· çb çcos(Ða, b) = x1 x2 + y1 y2 + z1z2. (3.13)
Скалярное произведение перестановочно: а×b=b×а. Если вектора перпендикулярны, то скалярное произведение равно нулю. Скалярное произведение векторов используют для определения длины вектора
а × a = x1x1+ y1y1 + z1z1 = x12+ y12 + z12 Þ ça ç=  (3.14)
(3.14)
Замечание: скалярное произведение обозначается знаком  .
.
Пример. Найти угол φ между векторами  и
и  , если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
, если М1(1, -2, -3), М2(-3, 1, 1), М3(3, 2, 2).
Решение. Для нахождения cosφ используем формулу
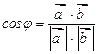
где  - скалярное произведение векторов
- скалярное произведение векторов 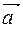 и
и  .
.
Определим координаты векторов 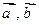 и cosφ:
и cosφ:
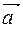 = (-3-1, 1+2, 1+3) =(-4, 3, 4),
= (-3-1, 1+2, 1+3) =(-4, 3, 4),  = (3-1, 2+2, 2+3) = (2, 4, 5),
= (3-1, 2+2, 2+3) = (2, 4, 5),
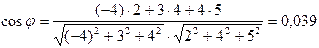 ,
,
φ = 87045'54".
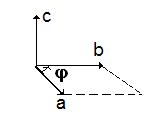
Векторным произведением векторов a и b называют такой вектор c = a ´ b, который:
1. лежит на прямой перпендикулярной плоскости векторов a и b,
2. имеет длину численно равную произведению длин векторов на синус угла между ними
çc ç = ça ç· çb çsin(Ða, b) = ça ç· çb ç sin(φ),
3. направление вектора c определяется по правилу буравчика: если вращать рукоять буравчика от первого вектора ко второму по наименьшему углу, то поступательное движение буравчика показывает направление вектора c.

Векторное произведение единичных векторов осей координат - ортов i, j, k равно
k = i ´ j, i = j ´ k, j = k ´ i. (3.15)
Векторное произведение не перестановочно: a ´ b = - b ´ a. Для коллинеарных векторов (лежащих на одной прямой) векторное произведение равно нулю a ´ b = 0, если a ççb. Для векторов заданных в форме проекций
с = a ´ b =  = i (y1z2 – y2z1) - j ( x1z2 – z1x2) + k ( x1y2 – x2y1). (3.16)
= i (y1z2 – y2z1) - j ( x1z2 – z1x2) + k ( x1y2 – x2y1). (3.16)
Длина вектора векторного произведение численно равна площади параллелограмма, построенного на векторах, как на сторонах: S = ça ç çb çsin(φ).
Замечание: векторное произведение обозначается знаком 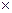 .
.
Смешанным произведением векторов a, b и c называется векторно-скалярное произведение
a´ b × c = a × b ´ c º a b c = 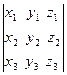 , (3.17)
, (3.17)
т. е. два вектора (первый – второй или второй – третий) перемножаются векторно, а третий вектор умножают на результат векторного произведения скалярно. В записи смешанного произведения знаки произведений обычно опускают. Смешанное произведение равно нулю, если векторы компланарны (лежат в одной плоскости). Смешанное произведение используют для вычисления объема параллелепипеда и пирамиды, построенной на векторах a, b, c.
Vпар = ê a b c ê; Vпир =  ê a b c ê.
ê a b c ê.
Пример. Даны координаты вершин пирамиды А1(1, -2, -3), А2(-3, 1, 1), А3(4, 3, -1), А4(3, 2, 2). Найти площадь грани А1 А2 А3 и объем пирамиды.
Решение. Площадь треугольника А1А2А3 найдем, используя геометрический смысл векторного произведения векторов
 ,
,
где 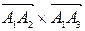 - векторное произведение векторов.
- векторное произведение векторов.
Вначале находим 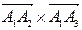
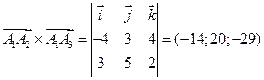 ,
,
а затем
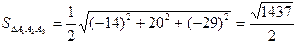 ед2.
ед2.
Объем пирамиды найдем, используя геометрический смысл смешанного произведения векторов
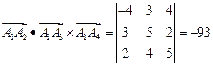 ,
,
следовательно, 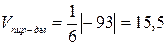 ед3.
ед3.
Дата добавления: 2022-01-22; просмотров: 163; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 (2.4)
(2.4)  ;
;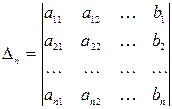 .
.