Графы соединений всегда связны.

Лекция 2

Формальное описание коммутационных схем

Речь идет об описании принципиальных электрических схем. В литературе по САПР принципиальные электрические схемы называют коммутационными. Связи в схеме соответствуют передаче электрических сигналов.

Принципиальную электрическую схему рассматриваем, как состоящую из множества элементов E = { e ₁ , e ₂ ,…, e _n }, соединенных между собой электрическими цепями из множества V = { v ₁ , v ₂ ,…, v_m }). Назовем такое представление коммутационной схемой (рис. 2.1).

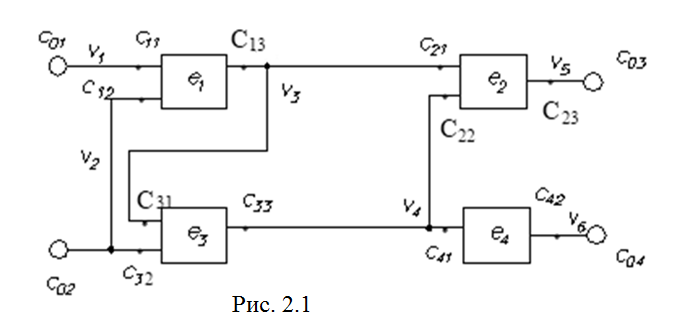
Каждый i -ый элемент имеет множество выводов С= { с _{i 1} ,с _{i 2} ,…, c_ik }. Внешние выводы схемы, служащие для связи с другими схемами (например, через электросоединитель), удобно представить фиктивным элементом e ₀.

Граф коммутационной схемы

Среди различных вариантов описания коммутационных схем наибольшей общностью и наглядностью обладает описание схемы в виде графа. Оно позволяет в целом ряде случаев найти адекватные задачи в теории графов и воспользоваться при разработке алгоритмов решения задач конструирования известными математическими методами.

Наиболее общим способом описания схем графами является граф коммутационной схемы (ГКС) G = ( E , V , C , F , W ).

Он несколько отличается от обычного линейного графа. Он содержит три типа вершин соответствующих:

- E – элементам;

- C – выводам элементов;

- V – цепям (комплексам).

Рёбра делятся на:

- элементные F;

- cигнальные W.

Элементные рёбра F определяют принадлежность выводов из множества C элементам из множества E и задаются парами вершин ( e_i , c_k ).

Сигнальные ребра W определяют вхождение выводов из С в отдельные цепи и описываются парами вершин( c_k , v_i ).

Для схемы, приведенной на рис. 2.1, (ГКС) приведен на рис. 2.2.

Описание ГКС матрицами

Т.к. ГКС содержит вершины и рёбра разных типов, его удобно описать двумя матрицами A и B.

Матрица A представляет цепи схемы и определяется следующим образом: А=║ a _ij║_{m xk} , где m - число цепей, k - число выводов в схеме. Строки матрицы соответствуют цепям, а столбцы – выводам элементов.

Элемент матрицы

aij=	если вывод с i принадлежит цепи vj в противном случае

Для графа, приведенного на рис. 2.2, матрица А имеет вид:

A =		c 01	c 02	c 03	c 04	c 11	c 12	c 13	c 21	c 22	c 23	c 31	c 32	c 33	c 41	c 42
	v 1	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0
	v 2	0	1	0	0	0	1	0	0	0	0	0	1	0	0	0
	v 3	0	0	0	0	0	0	1	1	0	0	1	0	0	0	0
	v 4	0	0	0	0	0	0	0	0	1	0	0	0	1	1	0
	v 5	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0
	v 6	0	0	0	1	0	0	0	0	0	0	0	0	0	0	1

 

Каждый столбец матрицы A содержит одну единицу, поскольку любой вывод может входить лишь в одну цепь. Число единиц в любой строке матрицы равно размеру соответствующей цепи.

Матрица B =║ b _ij║_nxk ,  выделяет подмножества выводов, принадлежащих отдельным элементам. Строки матрицы соответствуют элементам, а столбцы – выводам.

Элемент матрицы

bij	если вывод с j принадлежит элементу е i ; в противном случае

Для графа, приведенного на рис. 2.2, матрица B имеет вид:

B =		c 01	c 02	c 03	c 04	c 11	c 12	c 13	c 21	c 22	c 23	c 31	c 32	c 33	c 41	c 42
	e0	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0
	e1	0	0	0	0	1	1	1	0	0	0	0	0	0	0	0
	e2	0	0	0	0	0	0	0	1	1	1	0	0	0	0	0
	e3	0	0	0	0	0	0	0	0	0	0	1	1	1	0	0
	e4	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1

 

В каждом столбце матрицы В одна единица, т.к. вывод может принадлежать только одному элементу. Число единиц в строке равно числу выводов на соответствующем элементе.

Структуру ГКС можно задать одной матрицей T =║ t _ij║_{nxk 1} , строки которой соответствуют элементам, а столбцы выводам элемента, причём к₁ = max k_i , i =1, n .

Элемент матрицы t _ij представляет номер цепи, связанной с выводом c _j элемента e_i . Т.е. t ₂₃ – номер цепи, связанной с выводом c ₃ элемента e ₂ . Для нашей схемы:

T =		c 1	c 2	c 3	c4
	e0	1	2	5	6
	e1	1	2	3	-
	e2	3	4	5	-
	e3	3	2	4	-
	e4	4	6	-	-

 

Матрица T называется матрицей цепей. Для построения матрицы цепей необходимо каждой цепи присвоить номер.

Существуют упрощенные модели схем. Так, при компоновке элементов в конструктивные узлы можно не рассматривать выводы элементов, а рассматривать только сами элементы. Тогда элементные рёбра можно устранить, т.е. вершины - как бы «стянуть» в элементы (убираем выводы элементов, а цепи обозначаем точками). Тогда можно построить граф элементных комплексов (ГЭК) G ¹ = ( E , V ¹ , W ) Здесь множества вершин соответствуют:

- Е - элементам;

- V¹ - элементным комплексам;

- W - сигнальным рёбрам.

Элементный комплекс V ' _j - подмножество элементов из E = { e ₁ , e ₂ ,…, e _n }, соединенных цепью j , j =1, M . Элементные комплексы могут содержать общие элементы, то есть V ' _j Ç V ' _j ¹ 0, i ¹ j . Число элементов в комплексе V ' _j назовем размером элементного комплекса p ' _j.

ГЭК для схемы рис. 2.2 имеет вид:

Описать множества цепей (комплексов) этого графа

V₁={e₀,e₁}; V₂= { }; V₃={ }; V₄={ }; V₅={  }; V₆={   }

Для описания ГЭК удобно воспользоваться матрицей Q =║ q _ij║_nxm, строки которой соответствуют элементам, а столбцы элементным комплексам:

qij	, если элемент е i принадлежит цепи vj 1 (связан с ней); в противном случае

 

В нашем случае:

Q =		V 1 1	V 2 1	V 3 1	V 4 1	V 5 1	V 6 1
	e0	1	1	0	0	1	1
	e1	1	1	1	0	0	0
	e2	0	0	1	1	1	0
	e3	0	1	1	1	0	0
	e4	0	0	0	1	0	1

 

 

Описание ГКС гиперграфами

Коммутационную схему можно также упрощенно описать с помощью гиперграфов.

Гиперграф — обобщённый вид графа, в котором каждым ребром могут соединяться не только две вершины, но и любые подмножества вершин.

С математической точки зрения, гиперграф представляет собой пару H = ( E , V ), где E - непустое множество объектов некоторой природы, называемых вершинами гиперграфа, а V - семейство непустых (необязательно различных) подмножеств множества E, называемых рёбрами гиперграфа.

Гиперграфы применяются, в частности, при моделировании электрических схем.

Пример гиперграфа приведен на рис. 2.4.

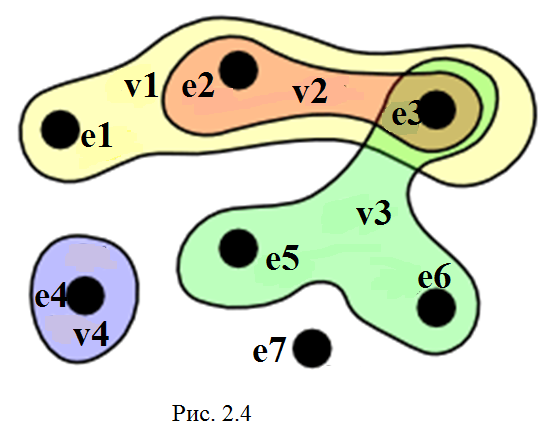
E = { e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ , e ₇ }

V = { v ₁ , v ₂ , v ₃ , v ₄ } = {{ e ₁ , e ₂ , e ₃ } , { e ₂ , e ₃ } , { e ₃ , e ₅ , e ₆ } , { e ₄ }}

Граф H = ( E , V ) называется гиперграфом, если он состоит из множества вершин Е={е₁,е₂,…,е _n } и множества рёбер V ={ v _1, v _2, …, v_m }. Причём каждое ребро v_i Î V представляет собой некоторое подмножество множества вершин, т.е. v_i Í E, v_i ¹ пусто,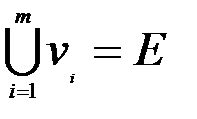

В гиперграфе H =( E , V ) две вершины считаются смежными, если существует ребро V, содержащее эти вершины. Два ребра смежные, если их пересечение – непустое множество.

Для графа H =( E , V ), приведенного на рис. 2.5,

½ E ½ =7, ½V ½ = 4.

Е={ e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ , e ₇ }

V ₁ ={ e ₁ , e ₂ , e ₃ , e ₄ }, V ₂ ={ e ₂ , e ₃ , e ₆ , e ₇ }, V ₃ ={ e ₄ , e ₅ }, V ₄ ={ e ₅ , e ₇ }.

Здесь, например, вершиныe₁ и e ₂ смежные, т.к. они связаны с ребромV ₁. v ₁ , v ₂ – смежные рёбра, т.к. их пересечение даёт множество { e ₂ , e ₃ }.

Гиперграф может быть описан матрицей инцидентности I ( H )= ║ a _ij║_nxm , строки которой соответствуют вершинам графа, а столбцы – его ребрам.

aij	1, если ei є Vj , 0 в противном случае.

Для гиперграфа с рис. 2.5 матрица инцидентности имеет вид:

I ( H )=		V 1	V 2	V 3	V 4
	e 1	1	0	0	0		V1 = {e1, e2, e3, e4} V2 = {e2, e3, e6, e7} V3 = {e4, e5} V4 = {e5, e7}
	e 2	1	1	0	0
	e3	1	1	0	0
	e4	1	0	1	0
	e5	0	0	1	1
	e6	0	1	0	0
	e7	0	1	0	1

 

 

 

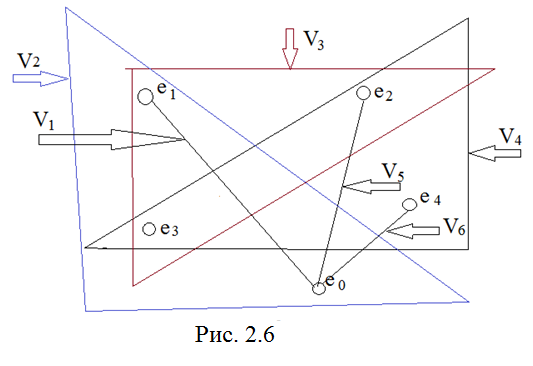
Представим теперь коммутационную схему в виде гиперграфа. В такой модели каждому ребру гиперграфа H взаимно - однозначно соответствует определённая цепь. Каждое ребро гиперграфа представляется в виде замкнутой кривой, охватывающей инцидентные ребру вершины. Если ребро инцидентно только двум вершинам, то их обычно соединяют отрезком. Тогда для схемы (рис. 2.2) гиперграф имеет вид (рис. 2.6):

E = { e ₁ , e ₂ , e ₃ , e ₄ , e ₅ , e ₆ , e ₇ }

V = { v ₁ , v ₂ , v ₃ , v ₄ , v ₅ , v ₆ }

V ₁ ={ e ₀ , e ₁ }; V ₂ ={ e ₀ , e ₁ , e ₃ }; V ₃ ={ e ₁ , e ₂ , e ₃ };

V ₄ ={ e ₂ , e ₃ , e ₄ }; V ₅ ={ e ₀ , e ₂ }; V ₆ ={ e ₀ , e ₄ }

V = {{ e ₀ , e ₁ } , { e ₀ , e ₁ , e ₃ } , { e ₁ , e ₂ , e ₃ } , { e ₂ , e ₃ e ₄ } , { e ₀ , e ₂ } , { e ₀ , e ₄ }}

 

Граф Кенига

Любому гиперграфу H может соответствовать так называемый граф Кенига G = {E V, U}. Это двудольный граф, состоящий из двух подмножеств вершин E и V, где E – множество вершин гиперграфа, а V – множество его рёбер. Подмножества E и V являются подмножествами несмежных вершин, т.е. между их элементами нет связей (рёбер). Вершины же e_iєE и V_jєV смежные только тогда, когда в гиперграфе вершина e_i принадлежит ребру V_j. Для схемы с рис. 2.2 двудольный граф имеет вид (рис. 2.7).

 

e ₀ Ì V ₁ , V ₂ , V ₅ , V ₆ ;

e₁ Ì V₁, V₂, V₃;

e₂ Ì V₃, V₄, V₅, V₆;

e₃ Ì V₂, V₃, V₄, V₆;

e ₄ Ì V ₄ , V ₆ ;

 

 

 

 

 

Взвешенный граф схемы

Чаще других используется более простое представление электрической схемы, когда элементам схемы соответствуют вершины графа e є E , а электрические цепи представляются рёбрами u є U. Пусть схема имеет вид рис. 2.8:

 

В таком графе каждый узел, т.е. сложная цепь, соединяющая три и более элемента, представляется полным графом с числом рёбер n ( n -1)/2, где n - число элементов цепи (рис. 2.9).

Т.е. каждый элементный комплекс в ГЭК представляется полным графом.

 

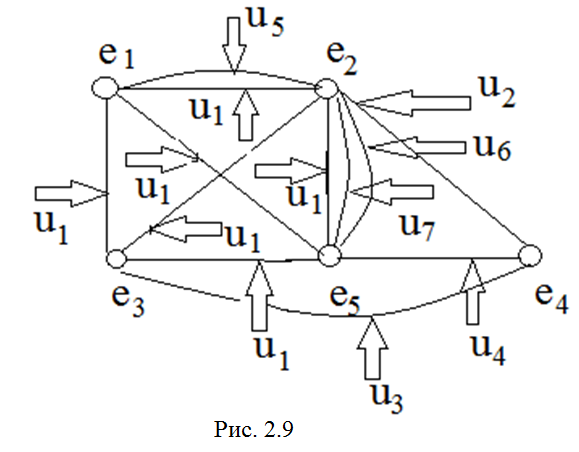
U₁={e₁,e₂,e_3,e₅} U₂={e₂,e₄} U₃={e₃,e₄}

U₄={e₄,e₅} U₅={e₁,e₂} U₆={e₂,e₅} U₇={e₅,e₂}

 

 

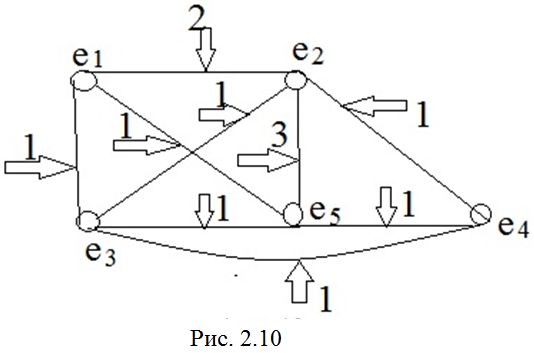
Далее перейдём от полученного мультиграфа к взвешенному графу, приписав каждому ему ребру u_ij «вес» z _ij , равный числу элементарных соединений между вершинами e_i и e_j . Получим взвешенный граф схемы (ВГС) (рис. 2.10).

 

 

Взвешенный граф схемы может теперь быть описан с помощью матрицы смежности R = ║ r _ij║_nxn, строки и столбцы которой соответствуют вершинам ВГС.

В нашем случае:

R=		e 1	e 2	e 3	e 4	e5
	e1	0	2	1	0	1
	e2	2	0	1	1	3
	e3	1	1	0	1	1
	e4	0	1	1	0	1
	e5	1	3	1	1	0

 

 

Представление сложных цепей полным графом вносит избыточность информации, т.к. в действительности элементы соединяются в виде дерева.

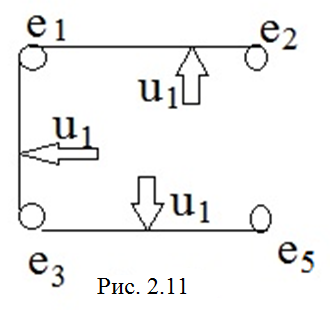
Модификацией мультиграфовой модели и ВГС является модель, представляемая графом, в котором полные подграфы, моделирующие цепи u Ì U , заменяются покрывающими их деревьями. Такая модель проще, но сложностью является выбор одного из n^{n -2} покрывающих деревьев, для каждого полного графа. Например, для цепи U ₁, можно выбрать такое дерево - рис. 2.11.

 

Применение ГКС, ГЭК, ВГС

ГКС – является наиболее полным и точным описанием и входит в исходную информацию САПР. Непосредственно используется при решении задачи трассировки. ГКС применяется для решения задачи размещения, когда надо учитывать размеры элементов и положения их выводов. Можно для размещения сначала использовать модели ГЭК и ВГС, а для получения окончательного решения ГЭК и ГКС. Для решения задач компоновки информация о точном расположении выводов на элементах не требуется. Поэтому наиболее часто используется ВГС и ГЭК. Причём ГЭК более соответствует физическому содержанию, а ВГС при описании его матрицей смежности наиболее легко реализуется на компьютере.

 

Графы монтажных соединений

Помимо графов для описания принципиальных схем используют графы монтажных соединений. О них будем говорить в разделе разводки цепей. Сейчас отметим их свойства:

Графы соединений всегда связны.

2. Графы соединений всегда связны чаще всего не содержат циклов, т.е. являются деревьями. Это связано с тем, что удаление любого ребра в цикле не нарушает электрического соединения. Правда, в монтаже электрокоробок применяются и замкнутые цепочки.

3.
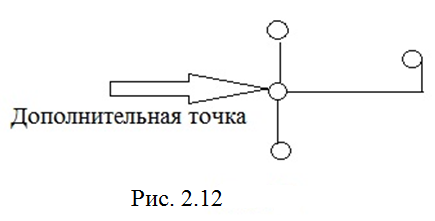
При печатном монтаже помимо выводов элементов используют дополнительные точки ветвления. Так образуются связи «вывод - проводник», «проводник - вывод», т.е. соединения имеют вид (рис. 2.12):

 

Такие деревья называются деревьями Штейнера.

 

Оглавление

Лекция 2. 1

Формальное описание коммутационных схем.. 1

Граф коммутационной схемы.. 2

Описание ГКС матрицами. 4

Описание ГКС гиперграфами. 10

Граф Кенига. 16

Взвешенный граф схемы.. 18

Применение ГКС, ГЭК, ВГС.. 23

Графы монтажных соединений. 24

 

 

---

Дата добавления: 2022-01-22; просмотров: 26; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!