Основные понятия теории графов

⇐ ПредыдущаяСтр 2 из 2

Граф G состоит из множества вершин Х (точек) и множества ребер U (линий) соединяющих между собой все или часть вершин. Обозначение графа G =( X ; U ). Запись u_ij Î U означает, что ребро графа u_ij=(x_i , x_j ) образовано парой вершин x_i и x_j, x_i Î X, x_j Î X. Таким образом, ребра - это упорядоченные пары вершин.

С помощью графов можно отразить наиболее общие свойства объектов (топологические свойства), отвлекаясь от их геометрических форм и размеров.

Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называется ориентированным графом. Для такого графа u_kj=(x_k , x_j ) ¹ ( x_j , x_k )= u_jk - это различные ребра

Если ребра не имеют ориентации, граф называется неориентированным.

Для него u_kj=(x_k , x_j )=( x_j , x_k )= u_jk.

Пример:

Вершины: здания; ребра: прямые улицы

В нашем курсе изучаются неориентированные графы. Две вершины x_i и x_j называются смежными, если существует ребро u_ij Î U, соединяющее эти вершины. Другими словами, смежными называются вершины, прилегающие к одному и тому же ребру.

Ребро u_ij инцидентно вершинам x_i , x_j, если оно связывает эти вершины. Ребра u_kl , u_lm называются смежными, если они имеют общую вершину (в примере вершина l).

Мультиграф – граф, любые две вершины которого связаны более чем одним ребром. В таком графе ребра, связывающие одну и ту же пару вершин, называются кратными. Мультичисло - наибольшее число кратных ребер в графе.

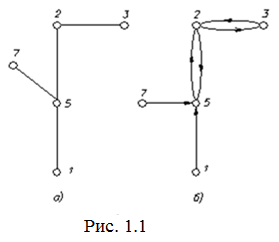
Петли – ребра графа, у которых обе концевые вершины совпадают, то есть u_ij=(x_i , x_j ), i = j (рис. 1.2).

Число ребер, инцидентных некоторой вершине, называют степенью вершины, обозначается p ( x ). Для графа на рис 1(а) p ( x ₅ )=3, p ( x ₁ )=1. Легко увидеть, что если сложить степени всех вершин графа, то получится четное число равное удвоенному числу ребер, так как каждое ребро участвует в сумме 2 раза. Этот результат называют леммой Эйлера о рукопожатиях (если несколько человек обменялись рукопожатием, то число пожатых рук – четно). Из этой леммы следует, что

В любом графе число вершин нечетной степени всегда четно.

Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.

Доказательство леммы. Заметим, что сумма степеней всех вершин в графе (или мультиграфе без петель) должна быть четной. Это следует из того, что если взять вершины, вообще не связанные друг с другом, то сумма степеней этих вершин равна нулю. Прибавляя любое ребро, которое связывает две вершины, увеличиваем сумму всех степеней на 2 единицы. Таким образом, сумма всех степеней вершин четна. Удаляя из этой суммы степени четных вершин, получим, что сумма степеней нечетных вершин, должна быть четной. Это значит, что само число таких вершин должно быть четным. Лемма доказана.

Изоморфизм графов

Графы на рис. 1.3 все выглядят как различные, но каждый из них можно перерисовать так, чтобы он стал (если не обращать внимание на обозначение вершин) идентичен другому. То есть все эти графы в некотором смысле «эквивалентны», имеют одинаковую структуру. Определим более точно характер этой «эквивалентности».

(а) (б) (в) Рис. 1.3. Изоморфные графы

Графы G =( X , U ) и G '=( X ', U ') изоморфны (пишут G @ G '), если существует взаимно-однозначное соответствие между множествами X и X ', сохраняющее смежность вершин (т.е. такое соответствие, при котором вершины x_i и x_j из множества X смежны тогда и только тогда, когда смежны соответствующие им вершины x ' _i и x ' _j из множества X ').

Изоморфизм графа рис. 1.3 (а), к графу рис.1.3 (б) обнаруживается, если задать следующее соответствие между вершинами:

а1-б1, а2-б5, а3-б6, а4-б3, а5-б2, а6-б4

(1.1)

Посмотрим, как это делается.

Для рис. 1.3(а) перечень неповторяющихся ребер:

(а1,а4) (а1,а5) (а1,а6) (а2,а4) (а2,а5) (а2,а6) (а3,а4) (а3,а5) (а3,а6)

(1.2)

Для рис. 1.3(б) перечень неповторяющихся ребер:

(б1,б3) (б1,б2) (б1,б4) (б5,б3) (б5,б2) (б5,б4) (б6,б3) (б6,б2) (б6,б4)

(1.3)

Если к (1.2) применить выражение (1.1), то получится выражение (1.3), т.е. графы на рис. 1.3 (а) и рис. 1.3(б) изоморфны.

Установить изоморфизм графа рис. 1.3(в), к графам на рис. 1.3 (а) и рис. 1.3(б) предлагается самостоятельно, определив надлежащее соответствие между их вершинами.

Для рис. 1.3(в) перечень неповторяющихся ребер:

(в1,в2) (в1,в4) (в1,в5) (в3,в2) (в3,в4) (в3,в5) (в6,в2) (в6,в4) (в6,в5)

(1.4)

При сопоставлении выражений (1.2) и (1.4), получается выражение (1.5) устанавливающее изоморфизм графа на рис. 1.3(в), к графу на рис. 1.3 (а):

а1-в1, а2-в3, а3-в6, а4-в2, а5-в4, а6-в5

(1.5)

При сопоставлении выражений (1.3) и (1.4), получается выражение (1.6) устанавливающее изоморфизм графа на рис. 1.3(в), к графу на рис. 1.3 (а):

б1-в1, б2-в4, б3-в2, б4-в5, б5-в3, б6-в6

(1.6)

Классификация графов

Полный граф – граф, у которого все вершины попарно смежные (рис. 1.4.). Так как для полного графа p ( x ₁ )= p ( x ₂ )= …= p ( x_n )= n -1, то число ребер в таком графе

(1.4)

Связный граф - неориентированный граф, у которого из любой вершины есть путь в любую другую вершину (путь может состоять из любого количества рёбер). На рис. 1.5 граф является связным.

Несвязанный граф – граф, состоящий из отдельных фрагментов. Если у графа на рис 1.5 удалить ребро между вершинами 4 и 5, то связным он не будет - из вершины 5 нельзя будет попасть ни в какую другую вершину.

Изолированная вершина – вершина, которой не инцидентно ни одно ребро.

Пустой граф – граф, состоящий только из изолированных вершин.

Висячая вершина – вершина степень, степень которой равна 1.

Граф G '=( X ', U ') называется частью графа G =( X , U ), если X ' Í X , U ' Í U и обозначается G ' Í G , т.е. часть графа – это граф, полученный из исходного графа исключением некоторых вершин и некоторых ребер.

Часть графа G '=( X ', U ') называют подграфом графа G =( X , U ), если X ' Í X, а множество ребер U ' Í U образовано всеми ребрами, соединяющими между собой только вершины из X ', т.е. подграф - граф, полученный из исходного графа исключением некоторых вершин и всех инцидентных им ребер.

Часть графа G '=( X ', U ') называют суграфом графа G =( X , U ), если X ' = X , а U ' Í U, т.е. суграф - граф, полученный из исходного графа исключением некоторых ребер.

Объект G_i =( X_i , U_i ), называется куском графа G =( X , U ), если X_i Í X , U_i Í U, причем U_i=U_ii È U_ij, где U_ii-множество ребер соединяющих вершины из X_i между собой, а U_ij - множество ребер, один конец которых принадлежит X_i, а второй X \ X_i, т.е. X_i - подмножество X, а в U_i входят все ребра из U, инцидентные X_i . Другими словами, кусок графа G(Z,U) – это граф Q(X,Y), являющийся частью исходного графа такой, что X — подмножество Z, а в Y входят все ребра из U, инцидентные X.

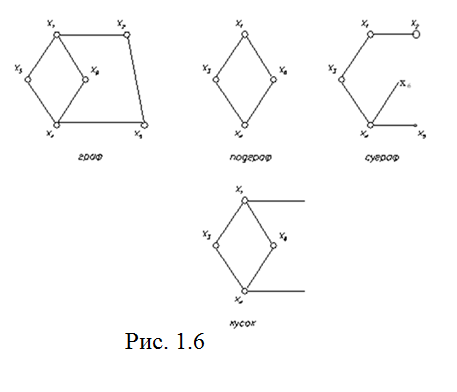
Пример:

Цепи и циклы в графах

Двигаясь по ребрам графа G ( X , U ), можно переходить из вершины в вершину. Любая последовательность ребер, получаемая при этом, называется маршрутом, то есть последовательность ( x ₀ , x ₁ )( x ₁ , x ₂ )…( x_n , x_n -1), в которой любые два соседних ребра смежные - маршрут.

Цепь – маршрут, в котором все ребра различны.

Простая цепь – цепь, в которой все вершины различны.

Цикл - цепь, в которой совпадают начальная и конечная вершины.

Дерево - связный граф без циклов. В дереве любые две вершины связаны единственной цепью. Дерево, построенное на n вершинах, имеет n-1 ребер.

Лес - совокупность деревьев.

Пример:

В графах выделяют два замечательных цикла: эйлеров и гамильтонов.

Граф называется эйлеровым, если для всякой вершины графа найдется маршрут начинающейся и заканчивающейся в этой вершине и проходящий через каждое ребро только один раз. Такой маршрут называется эйлеровым циклом.

Задача возникла из следующего примера. В XIII веке жители Кенигсберга, прогуливаясь по мостам реки, Прегель пытались решить задачу: можно ли обойти все мосты, проходя по каждому из них только один раз (рис. 1.8)

Задача состоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра - с мостами, которыми связаны эти части.

Эйлеру удалось доказать, что искомого маршрута обхода города не существует.

Ответ может быть получен на основе следующей теоремы.

Теорема. Граф является эйлеровым тогда и только тогда, когда степени всех его вершин четные.

Как следует из рисунка, у графа, моделирующего схему мостов, все вершины имеют нечетную степень. Следовательно, эйлерова цикла в этом графе не существует.

Пример графа, имеющего эйлеров, цикл показан на рис. 1.9.

Граф называется гамильтоновым, если для каждой вершины графа найдется маршрут начинающейся и заканчивающей в этой вершине и проходящий через все вершины только один раз (при этом могут участвовать не все ребра). Такой маршрут называется гамильтоновым циклом.

В полном графе с числом вершин n»2 всегда существует гамильтонов цикл. Пример такого цикла приведен на рис. 1.10 - (x1,x4) (x4,x2) (x2,x5) (x5,x3) (x3,x1).

Гамильтоновы графы применяются для моделирования многих практических задач, например, служат моделью при составлении расписания движения поездов. Основой всех таких задач служит классическая задача коммивояжера: коммивояжер должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, сведя при этом затраты на передвижения к минимуму.

Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра - связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге. Для решения задачи необходимо найти гамильтонов цикл минимального общего веса.

Описание графов матрицами

Графу G ( X , U ), имеющему n вершин, можно поставить в соответствие квадратную матрицу R =║ r_ij║_nxn, элементы которой r_ij соответствуют числу ребер, соединяющих вершину x_i с вершиной x_j. Это матрица смежности. Она задает в числовом виде связь смежных вершин. Элемент r_ii определяет число петель вершины x_i .

Для графа, представленного на рис. 1.11 матрица смежности записывается в виде:

R =		x₁	x₂	x₃	x₄	x₅
	x₁	0	1	0	0	1
	x₂	1	0	0	2	1
	x₃	0	0	0	1	0
	x₄	0	2	1	0	1
	x₅	1	1	0	1	0

Матрица смежности обладает следующими свойствами:

- симметрична относительно диагонали;

- сумма элементов в строке или столбце равна степени вершины.

Матрица инцидентности S =║ s_ij║_nxm - матрица, строки которой соответствуют вершинам графа G ( X , U ), столбцы – его ребрам:

, если i вершина инцидентна j -му ребру u_j ; , если i вершина не инцидентна j -му ребру u_j;

где n – число вершин графа (n = card X );

m – число ребер графа (m = card U).

Для графа G (рис. 1.11) матрица инцидентности имеет вид:

		U₁	U₂	U₃	U₄	U₅	U₆	U₇
	x₁	1	0	0	1	0	0	0
S=	x₂	1	1	1	0	0	0	1
S=	x₃	0	0	0	0	0	1	0
	x₄	0	1	0	0	1	1	1
	x₅	0	0	1	1	1	0	0

В общем случае S не квадратная матрица. В каждом столбце матрицы S имеется две единицы, так как каждое ребро соединяет 2 вершины. Матрицы R и S однозначно задают информацию о графе.

Оглавление

Введение. 1

Понятие проектирования. 1

Структура САПР. 3

Классификация САПР по приложениям. 3

Виды обеспечения САПР. 4

Лекция 1. 7

Основные понятия теории графов. 7

Изоморфизм графов. 10

Классификация графов. 12

Цепи и циклы в графах. 16

Описание графов матрицами. 21

Дата добавления: 2022-01-22; просмотров: 34; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 12

Мы поможем в написании ваших работ!