Примеры и разборы решения заданий тренировочного модуля
Тема урока : «Степень с рациональным и действительным показателем. Тестовая самостоятельная работа»
Теоретический материал
Пример: вычислим 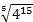
Мы можем представить  , тогда
, тогда

Таким образом, мы можем записать
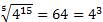 или
или 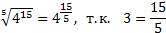
На основании данного примера можно сделать вывод:
Если n- натуральное число,  , m- целое число и частное
, m- целое число и частное 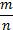 является целым числом, то при
является целым числом, то при 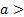 0 справедливо равенство:
0 справедливо равенство:
 .
.
Напомним, что r-рациональное число вида 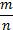 , где m- целое число , n- натуральное число. Тогда по нашей формуле получим:
, где m- целое число , n- натуральное число. Тогда по нашей формуле получим:

Таким образом, степень определена для любого рационального показателя r и любого положительного основания а.
Если  , то выражение
, то выражение  имеет смысл не только при
имеет смысл не только при 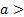 0, но и при а=0, причем,
0, но и при а=0, причем, 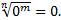 Поэтому считают, что при r
Поэтому считают, что при r  0 выполняется равенство
0 выполняется равенство 
Пользуясь формулой  степень с рациональным показателем можно представить в виде корня и наоборот.
степень с рациональным показателем можно представить в виде корня и наоборот.
Рассмотрим несколько примеров:
1. 
2. 
Отметим, что все свойства степени с натуральным показателем, которые мы с вами повторили, верны для степени с любым рациональным показателем и положительным основанием, а именно, для любых рациональных чисел p и q и любых 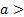 0 и
0 и  0 ы следующие равенства:
0 ы следующие равенства:
1. 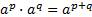 ;
;
2.  ;
;
3. 
4. 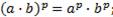
5. 


Разберем несколько примеров, воспользовавшись данными свойствами:
1. Вычислим: 

1. Упростить выражение:

В числителе вынесем общий множитель ab за скобки, в знаменателе представим корни в виде дробных показателей степени:
|
|
|
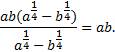
А теперь дадим определение степени с действительным показателем, на примере  .
.
Пусть  последовательность десятичных приближений с недостатком
последовательность десятичных приближений с недостатком  :
:

Эта последовательность стремится к числу  , т.е.
, т.е. 
Числа  являются рациональными, и для них определены степени
являются рациональными, и для них определены степени 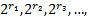 т.е. определена последовательность
т.е. определена последовательность 
Можно сделать вывод, что данная последовательность стремится к некоторому действительному числу, которое обозначают  , т.е.
, т.е.  .
.
Определение степени с действительным показателем.
При любом действительном х  и любом положительном а
и любом положительном а  ) степень
) степень  является положительным числом:
является положительным числом:
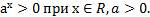
Но если основание степени а=0, то степень 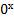 определяют только при
определяют только при 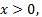 и считают, что
и считают, что 
При  выражение
выражение 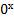 не имеет смысла.
не имеет смысла.
Для степени с действительным показателем сохраняются все известные свойства степени с рациональным показателем, из которых следует теорема.
Теорема. Пусть 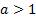 и
и 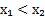 . Тогда
. Тогда 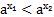 .
.
Доказательство:
По условию  . Поэтому, по свойству 1 имеем
. Поэтому, по свойству 1 имеем
а^(х₂)  . Умножив обе части этого равенства на положительное число
. Умножив обе части этого равенства на положительное число 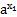 , получим
, получим  . По свойству умножения степеней получаем:
. По свойству умножения степеней получаем: 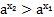 , т.е.
, т.е. 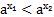 .
.
Из данной теоремы вытекают три следствия:
1. Пусть  Тогда
Тогда 
2. Пусть 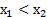 и
и 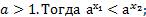
 .
.
1. Пусть  и
и 
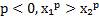 .
.
Эти теорема и следствия помогают при решении уравнений и неравенств, сравнении чисел.
|
|
|
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Сравнить числа 
Сравним показатели 
Т.к.  ,
,  и 12 < 18, то
и 12 < 18, то  .
.
Поэтому по теореме 
Пример 2. Решим уравнение
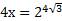
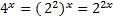 .
.
Поэтому уравнение можно записать так:

Получим,  , разделим на 2 обе части уравнения.
, разделим на 2 обе части уравнения.
Следовательно, 
Пример 3. Сравнить числа 
Избавимся от корней, для это возведем оба числа в шестую степень, т.к. шесть делится - наименьшее общее кратное двух и трех:
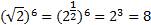
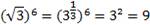
Т.к. 0<8<9 и  , то
, то  , т.е.
, т.е.  .
.
Пример 4.
Представить в виде степени с рациональным показателем:
 Ответ:
Ответ: 
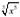 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 
Пример 5
Представить в виде корня из степени с целым показателем:
 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ:
Ответ: 
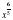 Ответ:
Ответ: 
Пример 6
Вычислить:
 Ответ:
Ответ: 
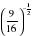 Ответ:
Ответ: 
 Ответ:
Ответ: 
 Ответ: не имеет смысла.
Ответ: не имеет смысла.
№57 вычислить. 2)  , 4)
, 4)  , 6)
, 6) 
№58 вычислить. 1) 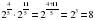 , 2)
, 2) 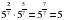 ,
,
3)  , 4)
, 4)  ,
,
5)  .
.
Записываем число, классная работа, тема урока
№59(2,4)
Вычислить:
2)  , 4)
, 4)  .
.
№62(2,4,6).
Представить в виде степени с рациональным показателем:
2) 
4) 
6) 
Дата добавления: 2022-01-22; просмотров: 228; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
