Формула применяется слева направо
Лекция 2. Неопределенный интеграл. Основные методы интегрирования.
Основные вопросы
1. Непосредственное интегрирование.
2. Метод подстановки (замены переменной).
3. Интегрирование по частям
.
Непосредственное интегрирование.
Непосредственным интегрированием называется отыскание неопределенного интеграла с помощью свойств неопределенных интегралов, таблицы основных интегралов и алгебраических преобразований подинтегральной функции.
Пример
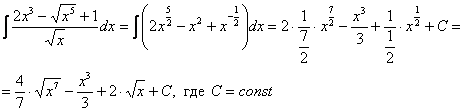
2. Метод подстановки (замены переменной).
Пусть требуется вычислить интеграл 
, где функция 
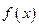определена на некотором промежутке 
.
Сделаем замену переменной в подынтегральном выражении, положив 
, где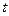 
- новая переменная, 
- функция, определенная и непрерывно дифференцируемая на некотором промежутке 
. Тогда получим: 
, (1)
После вычисления интеграла правой части (1) нужно вернуться к старой переменной 
обратной подстановкой 
.
Функцию выбирают таким образом, чтобы интеграл в правой части равенства (1) оказался проще исходного и мог быть вычислен.
Метод замены переменной в неопределенном интеграле реализуется двумя способами:
– а) Подведение функции под знак дифференциала ;
– б) Замена переменной .
По сути дела, это одно и то же, но порядок действий производится по-разному.
Пример 1- Подведение функции под знак дифференциала
|
|
|
Найти неопределенный интеграл . Выполнить проверку.
Смотрим на таблицу интегралов и находим похожую формулу: 
. Но у нас под синусом не просто буковка «икс», а сложное выражение. В этом случае интеграл сводят к табличному введением функции под знак дифференциала
Подводим функцию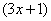 
под знак дифференциала:
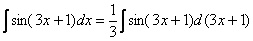
Раскрывая дифференциал, легко проверить, что:
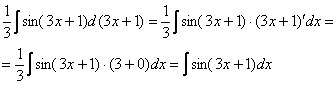
Фактически и 
Теперь можно пользоваться табличной формулой :
Выполним проверку. Открываем таблицу производных и дифференцируем ответ:
Получена исходная подынтегральная функция, значит, интеграл найден
Пример 2
Найти неопределенный интеграл. Выполнить проверку.
Анализируем подынтегральную функцию. Здесь у нас дробь, причем в знаменателе линейная функция («икс» входит в первой степени). Смотрим в таблицу интегралов и находим наиболее похожую формулу
: 
.
Подводим функцию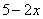 
под знак дифференциала:
Находим дифференциал: 
. ,
получается 
, а у нас просто «dx» значит, чтобы ничего не изменилось, надо домножить интеграл на 
.
Далее используем табличную формулу :
Проверка:
Получена исходная подынтегральная функция, значит, интеграл найден правильно.
Метод замены переменной в неопределенном интеграле
|
|
|
Переходим к рассмотрению общего случая – метода замены переменных в неопределенном интеграле.
Пример 3 -Метод замены переменной в неопределенном интеграле
Найти
Идея метода замены состоит в том, чтобы сложное выражение (или некоторую функцию) заменить одной буквой.
В данном случае напрашивается:
Отметим, что кроме буквы t можно использовать и букву 
и другие буквы
Так как осуществляется переход к новой переменной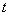 
, то в новом интеграле всё должно быть выражено через букву 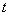, и дифференциал 
там не должен быть !!!
Следовательно, нужно превратить в некоторое выражение, которое зависит только от .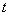
То есть, нам нужно найти дифференциал 
.
Так как , то
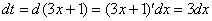
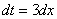
Отсюда выражаем :
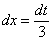
В итоге: 
А это уже табличный интеграл (естественно, она справедлива и для переменной ).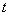
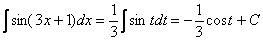
В заключении осталось провести обратную замену. Вспоминаем, что .
Чистовое оформление рассмотренного примера должно выглядеть примерно так:
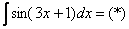
Проведем замену:
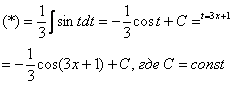
Этот же пример можно решить и первым способом-введением под знак дифференциала
В чем разница между этими методами? Принципиальной разницы нет. Это фактически одно и то же. Они отличаются только порядком действий .
|
|
|
Однако для ряда интегралов не так-то просто «ввести » функцию под знак дифференциала, поэтому используют замену переменной.
Пример 4
Найти
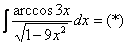
Смотрим в таблицу производных и находим арккосинус х:
.
Замечаем, что в подынтегральном выражении находится арккосинус и выражение, похожее на его производную.
Общее правило:
За 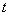обозначаем саму функцию (а не её производную).
В данном случае: 
. Осталось выяснить, во что превратится оставшаяся часть подынтегрального выражения 
.
Найдем
Или: 
Таким образом:
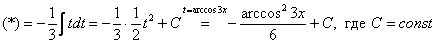
В этом примере подвести функцию под знак дифференциала уже не так-то просто.
Интегрирование по частям
Если функции 
и 
- дифференцируемые, то справедлива формула интегрирования по частям в неопределенном интеграле :
( * )
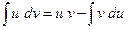При этом в подинтегральном выражении функции и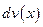 
выбирают таким образом, чтобы интеграл в правой части формулы (*) оказался проще исходного. Иногда формулу интегрирования по частям (*) приходится применять несколько раз.
Метод интегрирования по частям позволяет брать нетабличные интегралы, если подинтегральное выражение содержит произведение функций, а в ряде случаев – и частное. Отметим, что нет удобной формулы:
|
|
|
.
Зато есть такая:
– формула интегрирования по частям .
По частям берутся интегралы следующих видов:
1) 
, 
, 
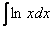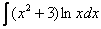– логарифм, логарифм, умноженный на какой-нибудь многочлен.
2) 
, 
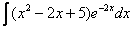– экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде 
– показательная функция, умноженная на многочлен
3) 
, 
, 
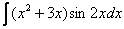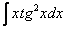– тригонометрические функции, умноженные на какой-нибудь многочлен.
4) 
, 
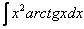– обратные тригонометрические функции.
Пример 5
Найти.
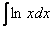
Решение:
Используем формулу интегрирования по частям:
Формула применяется слева направо
Смотрим на левую часть: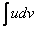 
. Очевидно, что в нашем примере 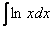(и во всех остальных, которые мы рассмотрим) что-то нужно обозначить за 
, а что-то за 
.
В интегралах рассматриваемого типа за всегда обозначается логарифм.
Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за мы обозначили логарифм, а за – оставшуюся часть подынтегрального выражения.
Следующий этап: находим дифференциал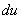 
:
Теперь находим функцию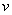 
. Для того чтобы найти функцию 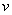необходимо проинтегрировать правую часть нижнего равенства 
:
Теперь открываем наше решение и пишем правую часть формулы:
.
Итак,
Выполним проверку. Для этого нужно взять производную от ответа:
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
Примеры на тему лекции
Пример
Задание. Вычислить неопределенный интеграл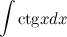 
Решение. Распишем подынтегральную сумму, используя тригонометрические функции (определение котангенса)
Внесем 
под знак дифференциала:
Полученный интеграл можно вычислить, используя табличный интеграл
В результате получим
Ответ. 
Дата добавления: 2021-12-10; просмотров: 107; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!