Введение вспомогательного аргумента.
Рассмотрим неоднородное уравнение вида
 , где
, где 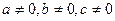 .
.
Если  ,то обе части уравнения делим на
,то обе части уравнения делим на 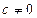 :
:

Вводим дополнительный угол 𝜑, такой, что 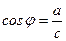 ,
,
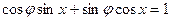 .
.
Применяя формулу 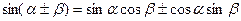 , получаем простейшее тригонометрическое уравнение
, получаем простейшее тригонометрическое уравнение

 .
.
При необходимости можно обозначить  ,
, 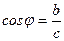
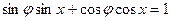 .
.
Применив формулу 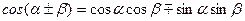 , получаем
, получаем

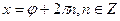 .
.
Сведение к однородному уравнению второго порядка.
Вновь рассматриваем неоднородное уравнение
 , где
, где 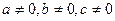 .
.
Если  , линейное неоднородное уравнение приводится к однородному уравнению второй степени с помощью перехода к функциям половинного аргумента:
, линейное неоднородное уравнение приводится к однородному уравнению второй степени с помощью перехода к функциям половинного аргумента:
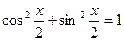 ;
; 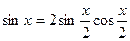 ;
; 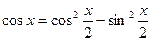
Исходное уравнение  запишем в виде:
запишем в виде:
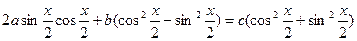 .
.
Универсальная тригонометрическая подстановка
Так как  ,
, 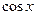 ,
,  ,
,  выражаются через
выражаются через  , уравнения вида
, уравнения вида 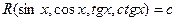 с помощью универсальной тригонометрической подстановки удается свести к алгебраическому уравнению. При этом используем формулы:
с помощью универсальной тригонометрической подстановки удается свести к алгебраическому уравнению. При этом используем формулы:
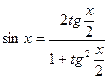 ;
; 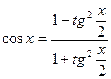 ;
;
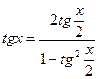 ;
; 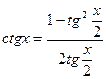
Обозначив  , где
, где 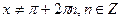 , получаем:
, получаем:
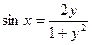 ;
;  ;
;  ;
; 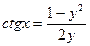 .
.
При этом следует иметь в виду, что замена  на
на 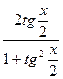 и
и 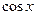 на
на  ведет к сужению области допустимых значений переменной, поскольку из рассмотрения исключаются значения х, при которых
ведет к сужению области допустимых значений переменной, поскольку из рассмотрения исключаются значения х, при которых 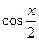 =0, т.е.
=0, т.е. 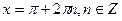 . Поэтому при применении универсальной тригонометрической подстановки необходимо дополнительно выяснить, являются или нет исключаемые из рассмотрения значения х корнями исходного уравнения.
. Поэтому при применении универсальной тригонометрической подстановки необходимо дополнительно выяснить, являются или нет исключаемые из рассмотрения значения х корнями исходного уравнения.
Пример. Решите уравнение
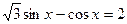 .
.
Решение
В данном уравнении 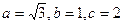 ,
,  . Вводим дополнительный угол. Для этого делим обе части равенства на 2:
. Вводим дополнительный угол. Для этого делим обе части равенства на 2:
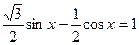
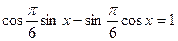
 ;
; 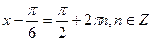
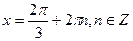 .
.
Ответ: 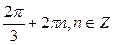 .
.
Пример. Решите уравнение
 .
.
Решение
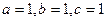 ,
, 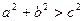 . Переходим к функциям половинного аргумента:
. Переходим к функциям половинного аргумента:

 ;
; 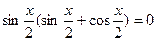
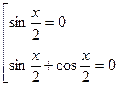
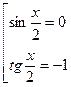
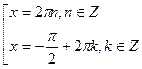
Ответ: 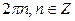 ;
; 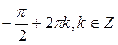 .
.
Пример. Решите уравнение
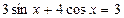 .
.
Решение
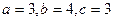 ,
, 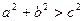 . Применим универсальную тригонометрическую подстановку.
. Применим универсальную тригонометрическую подстановку.
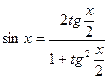 ;
; 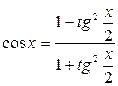 ;
;
 ;
; 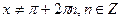 .
.
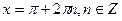 не является корнем исходного уравнения, следовательно, потери решений не произойдет.
не является корнем исходного уравнения, следовательно, потери решений не произойдет.
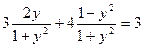

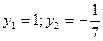

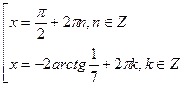
Ответ: 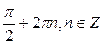 ;
; 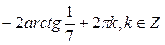 .
.
Дата добавления: 2021-12-10; просмотров: 56; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
