Основное тригонометрическое тождество
Конспект по теме «Тригонометрия для задания №9»
Тригонометрия – тема довольно обширная, но не сложная. Для начала вспомним, где мы с ней в первый раз познакомились.
Пример:
Найти: сos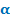 
, если b=3, c=5
Решение: Вспоминая, что косинус – это отношение прилежащего катета к гипотенузе, делим 3 на 5 и получаем сos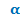 
= 3/5
Как легко запомнить?
Так, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои. Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение прилежащего катета к гипотенузе».
Проблема с определением косинуса решена.
Теперь пойдем дальше и поговорим про тригонометрическую окружность.
Числовой окружностью называют окружность единичного радиуса, точки которой соответствуют действительным числам, расставленным по следующим правилам:
1) Начало отсчета находится в крайней правой точке окружности;
2) Против часовой стрелки - положительное направление; по часовой – отрицательное.
Вспомним основы:
· Горизонтальная ось (ось оХ) – ось косинусов
· Вертикальная ось (ось ОY) – ось синусов
· Линия (ось) тангенсов проходит перпендикулярно Ох через точку (1;0)
· Линия (ось) котангенсов проходит параллельно Ох через точку (0;1)
Рассмотрим значения синуса и косинуса на окружности:
Давай представим, что мы находимся в точке А. Из точки А мы движемся против часовой стрелки по окружности, и при этом отмечаем расстояние, которое мы прошли. Длина числовой окружности равна 2π, поэтому, если мы пройдем всю окружность, то в этой же точке у нас уже будет расстояние 2π. Если пройдем половину - то π, четверть - π/2 и так далее.
|
|
|
Что будет, когда окружность «закончится» (т.е. мы сделаем полный оборот)?
Мы пойдем на второй круг! А когда и второй закончится, пойдем на третий и так далее. Поэтому на окружность можно нанести бесконечное количество чисел.
Как находить значения синуса и косинуса с помощью таблицы?
· косинус числа равен абсциссе точки на числовой окружности
· синус числа равен ординате точки на числовой окружности
Например, пусть нам нужно найти синус и косинус числа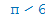 
.
Обозначим на числовой окружности точку со значением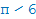 
. Если построить все точно и крупно, то можно убедиться, что абсцисса этой точки равна 0.8(6), что соответствует числу 
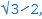а ордината равна 0,5, то есть 1/2. Таким образом можно найти значение любой точки на окружности.
Далее приведена таблица значений тригонометрических функций в
Зависимости от углов.
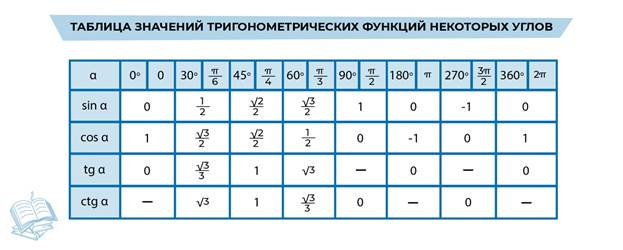
Как понять какие значения являются табличными? Есть такое
мнемоническое правило, которое называется “тригонометрия на
|
|
|
Ладони”.
Очень часто требуется знать наизусть значения cos, sin, tg, ctg для углов 0°, 30°, 45°, 60°, 90°.
Но если вдруг какое-либо значение забудется, то можно
воспользоваться правилом руки:
· Если провести линии через мизинец и большой палец,
то они пересекутся в точке, называемой “лунный бугор”.
Основное тригонометрическое тождество
Для любого угла 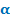верно утверждение:
sin2 α + cos2 α = 1
Эта формула связывает синус и косинус одного угла. Теперь, зная синус, мы легко найдем косинус — и наоборот. Достаточно извлечь квадратный корень:
Обратите внимание на знак «±» перед корнями. Дело в том, что из основного тригонометрического тождества непонятно, каким был исходный синус и косинус: положительным или отрицательным. Ведь возведение в квадрат — четная функция, которая «сжигает» все минусы (если они были).
Где это применяется? Да практически везде, ведь не даром это тождество основное.
Примеры решения задач с помощью тождества
Задача 1
Найдите sin 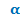, если известно следующее:
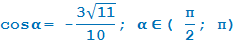
Решение:
1. Нам известен косинус, но неизвестен синус. Основное тригонометрическое тождество (в «чистом» виде) связывает как раз эти функции, поэтому будем работать с ним. Имеем:
|
|
|
sin2 α + cos2 α = 1 ⇒ sin2 α + 99/100 = 1 ⇒ sin2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
2. Для решения задачи осталось найти знак синуса. Поскольку угол α ∈ ( π /2; π ), то в градусной мере это записывается так: α ∈ (90°; 180°).
3. Следовательно, угол α лежит во II координатной четверти — все синусы там положительны. Поэтому sin α = 0,1.
Задача 2
Найдите tg α, если известно следующее:
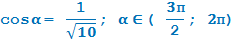
Решение:
Тангенс и косинус связаны уравнением, следующим из основного
тригонометрического тождества:
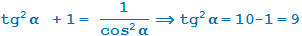
Получаем: tg α = ±3. Знак тангенса определяем по углу α.
Известно, что α ∈ (3 π /2; 2 π ). Переведем углы из радианной меры в градусную — получим α ∈ (270°; 360°).
Очевидно, это IV координатная четверть, где все тангенсы отрицательны. Поэтому tg α = −3.
А теперь поговорим про знаки тригонометрических функций в разных четвертях.
Легче всего работать с синусом и косинусом, там лишь достаточно провести перпендикуляр из соответствующей точки окружности на ось синуса или косинуса и можно сразу увидеть знак данной функции в этой четверти.
Для того, чтобы запомнить знак тангенса и котангенса, помним про их линии (оси):
|
|
|
· Тангенс положителен там, где его линия (ось) лежит выше Оу,
· Котангенс положителен там, где его линия (ось) лежит правее Оу.
Также не забываем про то, что:
· Тангенс = отношению синуса к косинусу,
· Котангенс = отношению косинуса к синусу.
Далее приведены знаки функций в разных четвертях:
Теперь вспомним про чётность и нечётность функций:
Формулы приведения
Формулы приведения позволяют свести вычисления синуса, косинуса, тангенса и котангенса любого угла к вычислению их значений для острого угла.
Формулы приведения для тригонометрических функций можно доказать с помощью формул сложения.
Например:
Применяя формулу сложения для синуса, получаем:
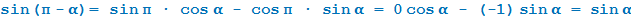
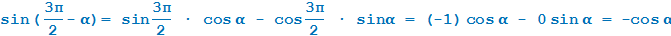
Таким образом можно доказать все оставшиеся формулы.
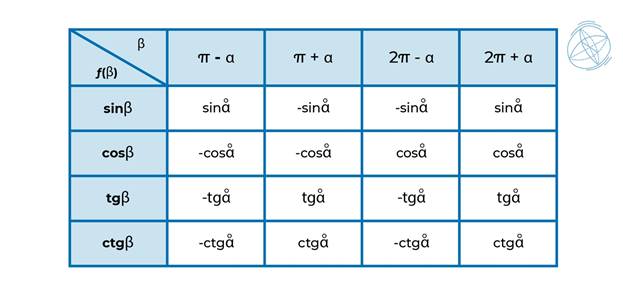
Формул приведения очень много. Таблицей пользоваться не всегда
удобно.
Запомнить их трудно, да в этом нет необходимости.
Достаточно запомнить одно правило:
1. Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида π + t, π − t, 2 π + t, 2 π − t, то наименование тригонометрической функции следует сохранить;
2. Если под знаком преобразуемой тригонометрической функции содержится сумма аргументов вида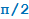 
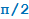+ t, 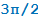− t, 
+ t,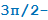 
t, то наименование тригонометрической функции следует изменить (на кофункцию: 
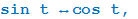t g t ↔ ct g t ;
3. Перед полученной функцией от аргумента t надо поставить тот знак, который имела бы преобразуемая функция при условии, что 0< t <2 π.
Как определить знак перед конечной функцией (плюс или минус)?
Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.
Пример
Выводим формулу приведения для cos (3π/2−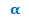 
) = ....
С исходной функцией понятно – косинус, а исходная четверть?
Для того, чтобы ответить на этот вопрос, представим, что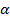 
– угол от 0 до π/2, т.е. лежит в пределах 0°… 90° (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол 3π/2− α?
Чтобы ответить на вопрос, надо от точки, обозначающей 3π/2, 
повернуть в отрицательную сторону на угол α.
В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус.
Поэтому перед итоговой функцией будет стоять минус:
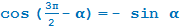
Дата добавления: 2023-02-21; просмотров: 28; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!