Постановка задачи интерполирования

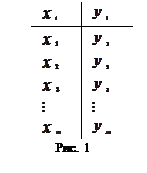
    Пусть дана табличная зависимость 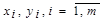 (рис. 1), где m – число экспериментальных точек.

Необходимо найти такую зависимость y = f_n ( x ) для которой все значения совпадают с табличными

f _n (x_i)=y_i , i=1, 2,…,m                                           (1)

где n – порядок f _n ( x_i ).

       

Шагом интерполирования называется величина h , определяемая следующим соотношением h = x_{i +1} - x_i .

Величина h может быть на всем рассматриваемом интервале постоянной (равностоящая интерполяция) и непостоянной (неравноотстоящая интерполяция). Значения f ( x_i ) называются узлами интерполирования.

Решение задачи интерполирования

 

     Положим, что f ( x )= f ( x , a ₀ ,..., a_n )                                         (2)

произвольная функциональная зависимость в общем случае нелинейная относительно неизвестных коэффициентов a ₀ , . . ., a_n (число определяемых коэффициентов не должно быть меньше числа экспериментальных точек).

Тогда задача интерполирования заключается в определении указанных коэффициентов исходя из условия (1).

Рассмотрим функциональную зависимость, линейную относительно коэффициентов a ₀ , . . ., a_{m -1}. Одним из распространенных классов функций, используемых при интерполировании, является класс многочленов. Функция f ( x ) при этом принимается в виде:

.                                       (3)

Метод неопределенных коэффициентов заключается в том, что если в уравнение (3) подставить табличные значения 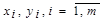, то определение коэффициентов сводится к решению системы m линейных уравнений:

                                                              (4)

где m = n +1.

Для решения системы линейных уравнений чаще всего используют методы Крамера, Гаусса, обращения матриц (см. приложение 1) и др.

ПРИМЕР

   Задание: интерполировать табличную зависимость, представленную на (рис. 2). Найти значение y в контрольной точке x = 3.

Решение:

Количество экспериментальных точек m =3. Следовательно, порядок интерполяционного многочлена n=2. Для n=2 формула (3) будет выглядеть:

.

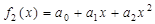Пользуясь полученной формулой, составим систему линейных уравнений:

или, подставив табличные значения, получим:

Решив полученную систему уравнений одним из методов решения систем линейных уравнений (см. приложение 1), получим значения неизвестных коэффициентов a ₀ =-1,59375, a ₁ =3,8125, a ₂ =-0,21875.

Тогда интерполяционная зависимость будет выглядеть:

.

При x=3 f ₂ ( x )=7,875.

Другим способом определения коэффициентов уравнения (3), позволяющим избежать решение системы уравнений (4), является построение интерполяционных многочленов, обеспечивающих равенство расчетных и экспериментальных значений функций в заданных узлах интерполирования, то есть точках (х _i , y_i ).

Интерполяционный многочлен Лагранжа

 

Интерполяционный многочлен Лагранжа, принимающий значения y ₁ , …, y_{n +1} в соответствующих точках, записывается в виде:

.                                                              (5)

Интерполяционный многочлен Лагранжа можно построить при любом расположении узлов интерполирования (точки могут быть неравноотстоящие).

ПРИМЕР

Рассмотрим предыдущую задачу.

Количество экспериментальных точек m =3. Порядок интерполяционного полинома Лагранжа n=2.

Формула (5) для n=2 будет выглядеть следующим образом:

 

или, подставив табличные значения, получим:

.

.

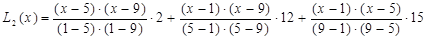Т.е. a₀=-1,59375, a₁=3,8125, a₂=-0,21875.

При x=3 L ₂ ( x )= 7,875.

 

---

Дата добавления: 2023-01-08; просмотров: 217; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!