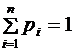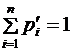По определению математического ожидания находим. Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме их ожиданий
. 
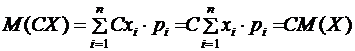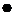
Свойство 3. Математическое ожидание суммы двух случайных величин равно сумме их ожиданий
.
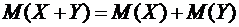Доказательство. Будем для простоты считать, что законы распределения случайных величин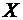 
и 
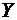заданы соответственно таблицами
Таблица 3. Таблица 4.
|
| 
| 
|
|
| 
| 
|
| |
| 
| 
|
| 
| 
|
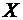
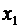
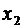
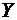
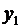
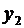
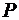
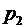
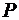
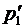
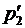
Тогда по определению математического ожидания
, 
.
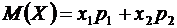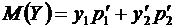Сумма случайных величин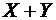 
будет иметь закон распределения вида
Таблица 5.
|
| 
| 
| 
| 
|
|
| 
| 
| 
| 
|
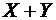
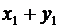
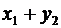
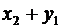
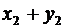
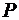
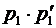
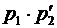
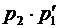
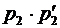
По определению находим математическое ожидание суммы двух случайных величин
.
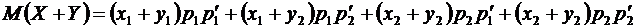Раскроем скобки и перегруппируем члены, получим
. ●
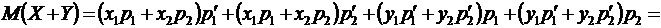
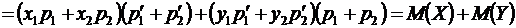Свойство 3 можно распространить с помощью метода математической индукции на случай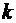 
случайных величин.
Свойство 4. Математическое ожидание суммы случайных величин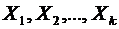 
равно сумме их ожиданий
. ●
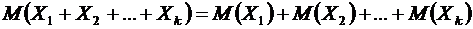Свойство 5. Математическое ожидание разности случайных величин 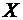и 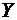равно разности их ожиданий
.
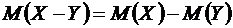Доказательство. Воспользовавшись свойствами 2 и 3 математического ожидания, имеем
. ●
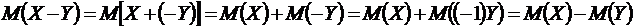Свойство 6. Математическое ожидание произведения двух независимых случайных величин равно произведению их ожиданий
.
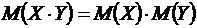Доказательство. Пусть как и в свойстве 3 законы распределения случайных величин 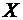и 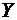заданы соответственно таблицами 3 и 4.
|
|
|
Произведение этих случайных величин будет иметь закон распределения вида
Таблица 6.
| 
| 
| 
| 
|
|
|
|
|
|
|
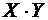
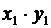
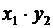
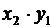
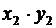
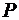
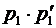
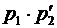
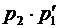
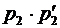
По определению находим математическое ожидание произведения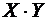 
.
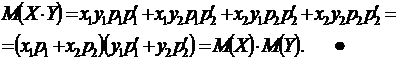
Методом математической индукции свойство 6 можно расширить на произведение любого конечного числа независимых случайных величин.
Свойство 7. Математическое ожидание произведения независимых случайных величин 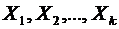равно произведению ожиданий
. ●
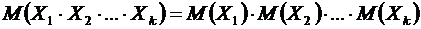Замечание. Отметим, что свойства 3 и 4 имеют место как для независимых, так и для зависимых случайных величин, а свойства 5 и 6 справедливы только для независимых случайных величин.
Определение. Разность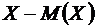 
называется отклонением случайной величины 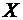от ее математического ожидания.
Из определения следует, что отклонение случайной величины 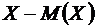является случайной величиной.
Свойство 8. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю
.
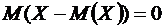Доказательство. По свойствам 5 и 1 математического ожидания находим
. ●
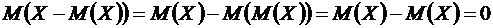Это свойство объясняет, почему математическое ожидание часто называют центром распределения случайной величины.
Свойство 9. Математическое ожидание среднего арифметического значения случайных величин равно среднему арифметическому значению их математических ожиданий
|
|
|
.
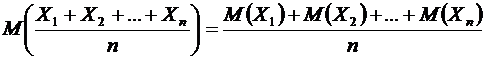Доказательство. Воспользуемся свойствами 2 и 4 математического ожидания, имеем
. ●
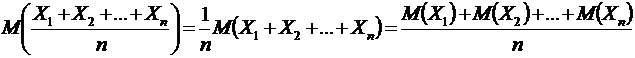Пример. Случайные величины 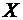и 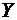заданы законами распределения
Таблица 7. Таблица 8.
|
| 4 | 6 |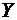
| 1 | 3 | |
|
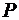
| 0,3 | 0,7 |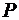
| 0,2 | 0,8 |
Найти математическое ожидание случайной величины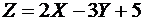 
.
Решение. Найдем по определению математические ожидания случайных величин 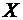и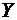
.
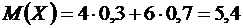
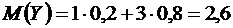Для того, чтобы найти математическое ожидание случайной величины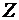 
, воспользуемся свойствами 1, 2, 3, 5 математических ожиданий
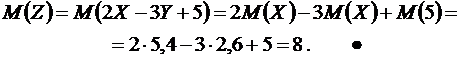
Дисперсия и ее свойства
Важное значение для характеристики случайных величин имеет дисперсия.
Определение. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
.
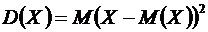Слово «дисперсия» означает «рассеяние», т.е. дисперсия характеризует рассеяние (разбросанность) значений случайной величины около ее математического ожидания.
|
|
|
Из определения следует, что дисперсия – это постоянная величина, т.е. числовая характеристика случайной величины, которая имеет размерность квадрата случайной величины.
С вероятной точки зрения дисперсия является мерой рассеяния значений случайной величины около ее математического ожидания.
Действительно, рассмотрим дискретную случайную величину, которая имеет конечное множество значений. Тогда, согласно определению, дисперсия вычисляется по формуле
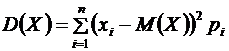. (2)
Если дисперсия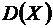 
мала, то из формулы (2) следует, что малы слагаемые 
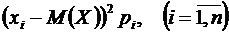. Поэтому если не рассматривать значения 
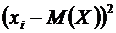, которым соответствует малая вероятность (такие значения практически невозможны), то все остальные значения 
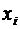мало отклоняются от математического ожидания 
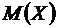. Следовательно, при малой дисперсии возможные значения случайной величины концентрируются около ее математического ожидания (за исключением, может быть, сравнительно малого числа отдельных значений). Если дисперсия 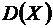велика, то это означает большой разброс значений случайной величины, концентрация значений случайной величины около какой-нибудь центра исключается.
Пример 1. Пусть случайные величины 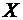и 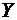имеют следующее законы распределения
|
|
|
Таблица 9. Таблица 10.
|
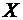
| -0,1 | 0 | 0,1 | 0,4 |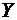
| -10 | 0,5 | 10 | |
|
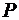
| 0,3 | 0,15 | 0,3 | 0,25 |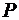
| 0,4 | 0,2 | 0,4 |
Найти математические ожидания и дисперсии этих случайных величин.
Решение. Воспользовавшись формулой для вычисления математических ожиданий, находим
.
.
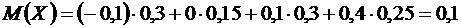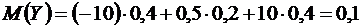С помощью формулы (2) вычислим дисперсии заданных случайных величин
.
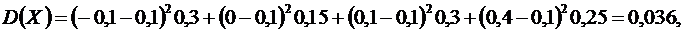
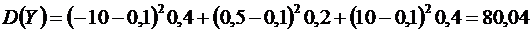Из полученных результатов делаем вывод: математические ожидания случайных величин 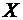и 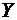одинаковы, однако дисперсии различны. Дисперсия случайной величины 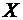мала и мы видим, что ее значение сконцентрированы около ее математического ожидания 
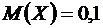. Напротив, значения случайной величины 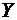значительно рассеяны относительно 
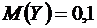, а поэтому дисперсия 
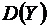имеет большое значение. ●
Свойства дисперсии
Свойство 1. Дисперсия постоянной величины равна нулю
.
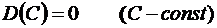Доказательство. Если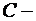 
постоянная величина, то по свойству 1 математиче-ского ожидания 
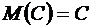, а поэтому
. ●
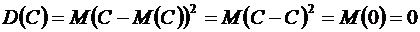Свойство 1 очевидно с вероятной точки зрения: так как постоянная величина изображается одной точкой на числовой оси 
, т.е. не имеет рассеяние, то и мера рассеяния постоянной величины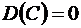 
.
Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат
.
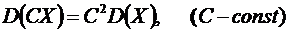Доказательство. Из определения дисперсии и свойства 2 математического ожидания получаем
. ●
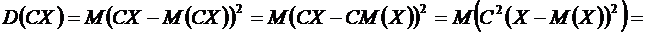
Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий
.
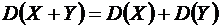Доказательство. Воспользуемся определением дисперсии и свойствами 3, 2 математического ожидания, имеем
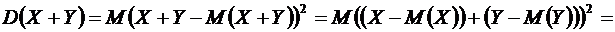
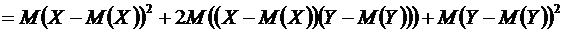(3)
Определение. Математическое ожидание произведения отклонений случайных величин 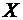и 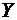от их математических ожиданий называется корреляционным моментомэтих величин
.
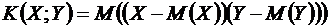Если случайные величины, величины 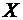и 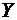независимы, то воспользовавшись свойствами 6 и 7 математических ожиданий, находим
.
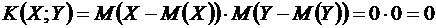Поэтому из формулы 3 имеем
,
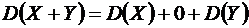откуда окончательно следует
. ●
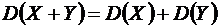С помощью метода математической индукции это свойство может быть распространено на случай любого конечного числа независимых случайных величин.
Свойство 4. Дисперсия суммы независимых случайных величин 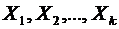равна сумме их дисперсий
. ●
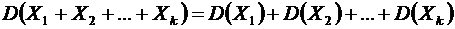Свойство 5. Дисперсия разности двух случайных независимых величин равна сумме дисперсий этих величин
.
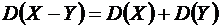Доказательство. На основании свойств 2 и 3 дисперсии имеем
. ●
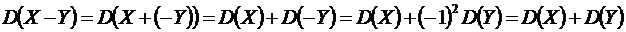Свойство 6. Дисперсия случайной величины равна математическому ожиданию
квадрата этой величины минус квадрат ее математического ожидания
.
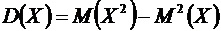(Эта формула применяется для вычисления дисперсии)
Доказательство. Воспользовавшись свойствами 1,2,3,5 математического ожидания, находим
. ●
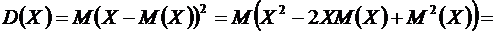
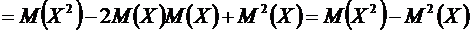Дата добавления: 2018-02-15; просмотров: 1620; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!