Завдання 2-го етапу Всеукраїнської олімпіади юних математиків 2004 р. Клас Знайдіть а, при яких відстань між вершинами парабол і менша
Клас
- Знайдіть а, при яких відстань між вершинами парабол
 і
і 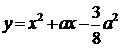 менша
менша 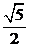 .
. - Розв’язати нерівність
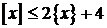 .(
.(  означає найбільше ціле число, що не перевищує х,
означає найбільше ціле число, що не перевищує х, 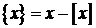 ).
). - У квадраті з площею 6 розташовані з прямокутника, кожний із площею 3. Довести що площа спільної частини принаймні двох із прямокутників не менша 1.
- Троє грають в таку гру. Кожний по черзі кладе на круглий стіл п’яти копійчані монети, монети можуть торкатися, але не повинні накладатися одна на одну. Програє той, чия монета не вміститься на столі. Довести, що перший та третій (за порядком ходів) гравці можуть так змовитись, що другий гравець завжди програватиме.
- Побудувати трикутник, знаючи його сторону, протилежний кут і висоту, яка проведена до іншої сторони.
- Нехай
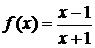 , а
, а 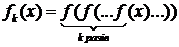 . Знайти
. Знайти 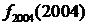 .
.
Завдання 2-го етапу Всеукраїнської олімпіади юних математиків 2004 р.
Клас
- Розв’язати рівняння
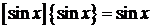 .(
.( 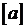 означає найбільше ціле число, що не перевищує а,
означає найбільше ціле число, що не перевищує а, 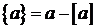 ).
). - Довжини сторін чотирикутника, який описано навколо кола радіуса r, утворюють геометричну прогресію. Обчисліть площу цього чотирикутника, якщо один з його кутів дорівнює b.
- На колі взято n точок і проведено всі можливі хорди, що сполучають ці точки. Відомо, що жодні три з проведених хорд не перетинаються в одній точці. На скільки частин розіб’ється круг?
- Нехай
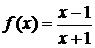 , а
, а 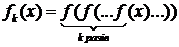 . Знайти
. Знайти 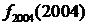 .
. - Застосовуючи теорему косинусів, знайти найменше значення виразу:
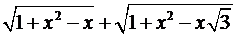 .
. - Одну з вершин правильного 2004 – кутника пофарбовано у чорний колір, а решту його вершин – у білий. За один крок дозволяється вибрати будь-яку зафарбовану у чорний колір вершину та змінити колір на протилежний у неї та ще у двох сусідніх із нею вершин. Чи можливо за декілька зазначених кроків перефарбувати всі вершини даного 2004 – кутника у білий колір?
Й етап Всеукраїнської олімпіади юних математиків 2004 р.
|
|
|
Відповіді та вказівки.
Клас
1. Відповідь. 636. Оскільки перша білочка з’їла найбільше горішків, а друга і третя з’їли 1269 горішків, то перша білочка з’їла не менше 636 горішків. Оскільки четверта білочка з’їла не менше 100 горішків, то перша з’їла не більше, ніж 2005– 1269 – 100 = 636 горішків. Отже, перша білочка з’їла 636 горішків.
2.

3. Можливі три випадки: правду сказала або Тетянка або Данилко, або Марійка. Якщо правду сказала Тетянка, то Марійка теж сказала правду, що суперечить умові. Отже, цей випадок не можливий. Якщо правду сказала Марійка, то Тетянка і Данилко повинні сказати неправду. Це можливо, якщо у Андрійка рівно 100 книг. Якщо правду сказав Данилко, то твердження Тетянки і Марійки невірні. Це можливо, якщо у Андрійка книг немає. Відповідь: 0 або 100.
4. Відповідь: другий (він має доповнювати ходи першого гравця до 6 сірників).
|
|
|
5. При діленні числа на 2004 остача може дорівнювати 0,1,2,…, 2003 – всього 2004 різних варіантів. Тому, за принципом Діріхле, серед 2005 чисел знайдуться принаймні два, які дають однакову остачу при діленні на 2004, а їх різниця буде ділитися на 2004 без остачі.
Клас
1. Відповідь:36.
2. Серед початкових чисел – непарних чисел непарна кількість. При кожному перетворенні кількість непарних чисел або лишається незмінною, або зменшується на 2. Тому останнє число неодмінно непарне.
|
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 |
| 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 |
| 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 |
| 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 |
| 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 |
| 6 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 |
| 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 |
4. а) Легко бачити, що кожне з цих чисел дорівнює 1 або –1. Для того, щоб їх добуток дорівнював додатному числу 1, треба, щоб кількість від’ємних множників була парною. З іншого боку, сума може дорівнювати, нулю, якщо кількість чисел (–1 ) дорівнює кількості чисел 1, тобто 11. Але 11 – число непарне. б)Нехай сума дорівнює 1. Кількість додатних доданків дорівнює n, кількості від’ємних доданків дорівнює 22–n. Тоді 1∙n–1(22– n) =1, тобто 2n–22=1, але 2n і 22 – парні числа. Тому їх різниця не може бути непарною.
|
|
|
5. Відкладемо вибрану монету, а решту порівну кладемо на шальки за допомогою гирьок домагатимуся рівноваги. Якщо відібрано справжню монету, то для цього необхідна парна кількість грамів, а інакше – непарна.
Клас
1. Відповідь: 46 см.
2. Нехай при десятковому записі числа 22004 було використано n цифр, а числа 52004 – m цифр, тобто 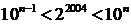 ,
,  . Тоді перемноживши данні нерівності, отримаємо
. Тоді перемноживши данні нерівності, отримаємо 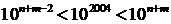 , звідси
, звідси
n+m–1=2004 і n + m=2005.
3. Якщо не всі числа на колі рівня ,то після виконання вказаної операції сума всіх n чисел зменшується (оскільки між кожними різними двома числами запишеться число, не більше, ніж найменше у парі). При цьому ця сума зменшиться на натуральне число. Але вона не може зменшуватись нескінченно, оскільки найменше можливе значення цієї суми не менше, ніж n. Отже, на якомусь кроці вказана сума перестане змінюватися. Це й означає, що всі числа на колі рівні.
|
|
|
4. Жодні три цифри числа рk не будуть однаковими лише тоді, коли кожна цифра буде використана двічі. Але тоді сума його цифр повинна дорівнювати 2∙(0+1+2+…+9)=90 і тому таке число має ділитись на 3. Але якщо просте число р>3, то рk не ділиться на 3.
5. Аналіз. Продовжимо один з катетів від прямого кута так, щоб одержати суму катетів. З’єднаємо одержану точку з третьою вершиною прямокутного трикутника. Одержимо трикутник, у якого один кут 45  і відомі дві сторони. Його можна побудувати, отже можна побудувати шуканий трикутник.
і відомі дві сторони. Його можна побудувати, отже можна побудувати шуканий трикутник.
Клас
1. Оскільки 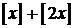
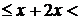
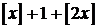 +1, то 3≤3х<5. Тому розв’язки рівняння знаходяться на проміжку
+1, то 3≤3х<5. Тому розв’язки рівняння знаходяться на проміжку 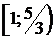 . Тоді
. Тоді 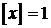 ,
, 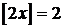 , звідки 2≤2х<3. Отже,
, звідки 2≤2х<3. Отже, 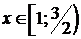 .
.
2. Першим ходом перший гравець сумістить центр столу і центр монети. Після довільного ходу другого гравця третій гравець покладе свою монету на місце, яке утвориться після повороту монети другого гравця на 120  за годинниковою стрілкою відносно центру столу, а потім перший – на 120
за годинниковою стрілкою відносно центру столу, а потім перший – на 120  проти годинникової стрілки.
проти годинникової стрілки.
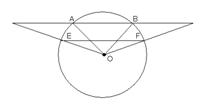
3. Нехай ОА і ОВ – два даних радіуса. Продовжимо відрізок АВ в обидві сторони так, що АС=ВD=АВ. ОС і ОD перетинає коло в точках Е і F. Очевидно що ЕF – шукана хорда (використовується гомотетія).
4. З умови 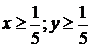 випливає, що х і у – натуральні числа. Зведемо рівняння до спільного знаменника і помножимо його на
випливає, що х і у – натуральні числа. Зведемо рівняння до спільного знаменника і помножимо його на 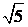 . Отримаємо рівняння
. Отримаємо рівняння 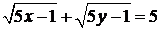 . Ліва частина сума невід’ємних чисел, то кожен доданок не більше 5. З умови
. Ліва частина сума невід’ємних чисел, то кожен доданок не більше 5. З умови 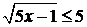 і
і 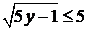 , найдемо , що х≤5; у≤5. Підбором знаходимо пари чисел (1;2) і (2;1), які задовольняють дане рівняння.
, найдемо , що х≤5; у≤5. Підбором знаходимо пари чисел (1;2) і (2;1), які задовольняють дане рівняння.
5. Переформулюємо задачу інакше: знайти остачу від ділення числа 22004 на100. Знайдемо послідовно остачі від ділення на 100 чисел вигляду 2n . Вона має вигляд:2, 4, 8, 16, 32, 64, 28, 56, 12, 24, 48, 96, 92, 84, 68, 36, 72, 44, 88, 76, 52, 4,…. Бачимо, що починаючи з другої остачі4 для n=22, остачі від ділення повторюються періодом 20. Оскільки 2004 при діленні на 20 дає остачу 4, то останні дві цифри числа 22004 такі ж, як дві остання цифри числа 2n, тобто 1 та 6.
6. Нехай n – число трикутників. Зауважимо, що 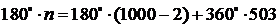 , де в правій частині рівності перший доданок дорівнює сумі внутрішніх кутів тисячокутника. Звідси n=2004.
, де в правій частині рівності перший доданок дорівнює сумі внутрішніх кутів тисячокутника. Звідси n=2004.
Клас
1. Абсциса вершини параболи 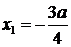 , а ордината
, а ордината 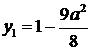 . Для другої параболи
. Для другої параболи 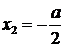 ,
, 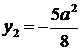 . Тоді відстань між вершинами цих парабол
. Тоді відстань між вершинами цих парабол 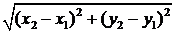 =
= 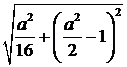 . Враховуючи умову, отримали, що а є розв’язком нерівності
. Враховуючи умову, отримали, що а є розв’язком нерівності 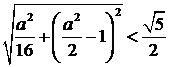 . Підкореневий вираз і права частина нерівності – додатні. Тому підносячи обидві частини нерівності до квадрату, отримаємо
. Підкореневий вираз і права частина нерівності – додатні. Тому підносячи обидві частини нерівності до квадрату, отримаємо 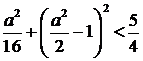 , звідки
, звідки 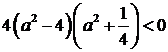 . Оскільки
. Оскільки  ,то наша нерівність рівносильна нерівності
,то наша нерівність рівносильна нерівності 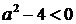 . Тому
. Тому 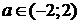 .
.
2. Запишемо нерівність у вигляді  . Оскільки
. Оскільки 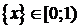 , тобто
, тобто 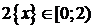 , то шукані х повинні задовольняти умові
, то шукані х повинні задовольняти умові 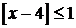 . При цьому очевидно, що всі значення х, при яких
. При цьому очевидно, що всі значення х, при яких 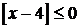 є розв’язками нашої нерівності і тоді х<5. Розглянемо випадок коли
є розв’язками нашої нерівності і тоді х<5. Розглянемо випадок коли 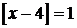 . Тоді 1≤х–4<2, 5≤х<6. При цьому
. Тоді 1≤х–4<2, 5≤х<6. При цьому 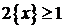 ,
, 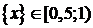 . Тоді
. Тоді 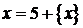 і
і 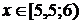 .
.
Відповідь: 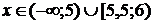 .
.
3. Нехай S12, S13, S23 – відповідно площі спільних частин першого і другого, першого і третього та другого і третього прямокутників. Тоді разом ці прямокутники покривають площу, не меншу за 3∙3 – (S12+ S13+S23), де 3∙3 = 9 – сума площ даних прямокутників (величину S12+ S13+S23 слід відняти, щоб не враховувати двічі площі спільних частин). Оскільки всі три прямокутники помістились у квадраті з площею 6, то 9 – (S12+ S13+S23) ≤ 6. Тому S12+S13+S23≥3. А отже, принаймні одне з чисел S12+S13+S23 не менше 1.
4. Першим ходом перший гравець сумістить центр столу і центр монети. Після довільного ходу другого гравця третій гравець покладе свою монету на місце, яке утвориться після повороту монети другого гравця на 120  за годинниковою стрілкою відносно центру столу, а потім перший – на 120
за годинниковою стрілкою відносно центру столу, а потім перший – на 120  проти годинникової стрілки.
проти годинникової стрілки.
5. Будуємо ГМТ, з яких основу видно під даним кутом (цьому ГМТ належить шукана вершина трикутника, далі будуємо ГМТ, з яких основу видно під прямим кутом (півколо) і з вершини при основі радіусом, який дорівнює висоті, проводимо дугу до перетину з цим півколом – одержимо основу висоти на бічній стороні. Подальша побудова очевидна.
6. Відповідь. 2004. 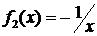 , а
, а 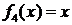 , то
, то 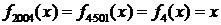 .
.
Клас
1. Дане рівняння рівносильне сукупності систем:
 або
або 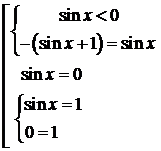 звідки маємо
звідки маємо 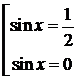 ,
, 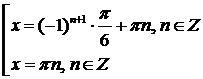 .
.
2. У описаного чотирикутника суми протилежних сторін рівні. Виходячи з цього, легко довести, що знаменник геометричної прогресії дорівнює 1. Отже даний чотирикутник ромб.
3. Сполучимо послідовно точки, взяті на колі, хордами і підрахуємо, на скільки частин розбивається діагоналями утворений n – кутник. Для цього діагоналі будемо проводити послідовно. Після проведення кожної діагоналі число частин збільшується на число, яке на одиницю більше від числа точок перетину, що з’являються після проведення однієї діагоналі. Число всіх діагоналей n–кутника дорівнює 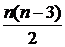 . А число точок перетину діагоналей n–кутника дорівнює
. А число точок перетину діагоналей n–кутника дорівнює 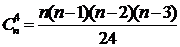 . Отже, круг розіб’ється на
. Отже, круг розіб’ється на 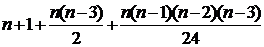 частини.
частини.
4. Відповідь. 2004. 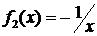 , а
, а 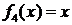 , то
, то 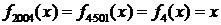 .
.
5. Розглянемо рівнобедрений прямокутний трикутник, у якого катет дорівнює 1, а на промені, який ділить прямий кут на 30 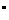 і 60
і 60 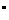 .Відкладемо відрізок х. Тоді відповідний відрізок є довжиною ламаної, яку утворюють відрізки, які лежать напроти кутів у 30
.Відкладемо відрізок х. Тоді відповідний відрізок є довжиною ламаної, яку утворюють відрізки, які лежать напроти кутів у 30 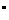 і 60
і 60 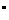 . Тоді зрозуміло, що довжина цієї ламаної мінімальна, коли це відрізок прямої, тобто гіпотенуза прямокутного трикутника зі стороною 1. Тому найменше значення виразу –
. Тоді зрозуміло, що довжина цієї ламаної мінімальна, коли це відрізок прямої, тобто гіпотенуза прямокутного трикутника зі стороною 1. Тому найменше значення виразу – 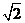 .
.
6. Легко бачити, що після кожного перефарбування кількість чорних вершин змінюється на парне число. Тому, якщо вказане перефарбування можливе, то воно складається з непарного числа кроків. Позначимо А1, А2,…, А2004, починаючи з вершини А1 чорного кольору. Нехай аk – кількість тих кроків, при яких центром зміни кольорів була вершина аk. Тоді 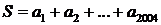 – це загальна кількість всіх кроків і вона, згідно доведеного, має бути непарним числом. Але
– це загальна кількість всіх кроків і вона, згідно доведеного, має бути непарним числом. Але 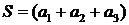 +
+ 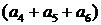 +…+
+…+  . Тут у кожних дужках суми трьох записаних доданків співпадають із загальною кількістю змін кольорів відповідно у вершинах А2, А5,…, А2003.Оскільки у них і спочатку, і в кінці колір буде білим, то кожна з цих сум, а з ними і S,є парною. Одержане протиріччя доводить неможливість вказаного перефарбування
. Тут у кожних дужках суми трьох записаних доданків співпадають із загальною кількістю змін кольорів відповідно у вершинах А2, А5,…, А2003.Оскільки у них і спочатку, і в кінці колір буде білим, то кожна з цих сум, а з ними і S,є парною. Одержане протиріччя доводить неможливість вказаного перефарбування
Дата добавления: 2018-02-18; просмотров: 716; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 6 мав би по одній клітинці кожного кольору і тоді клітинок кольору №2 мало б бути 72:6=12.Неважко порахувати, що насправді таких клітинок маємо 13. Отже, таке розрізання не можливе.
6 мав би по одній клітинці кожного кольору і тоді клітинок кольору №2 мало б бути 72:6=12.Неважко порахувати, що насправді таких клітинок маємо 13. Отже, таке розрізання не можливе.