Элементы теории классов групп.
Определение 49. Классом групп называется всякое множество групп, которое вместе с каждой своей группой  содержит и все группы, изоморфные ей.
содержит и все группы, изоморфные ей.
Если группа (подгруппа)  принадлежит классу групп
принадлежит классу групп  , то
, то  называют
называют  - группой (подгруппой).
- группой (подгруппой).
Определение 50. Операцией на классах групп называется отображение  множества классов групп в себя.
множества классов групп в себя.
Произведение операций определяется следующим образом:
 . И вообще:
. И вообще:  .
.
Рассмотрим следующие операции на классах групп:
 когда
когда  является подгруппой некоторой
является подгруппой некоторой  группы, то есть
группы, то есть 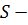 отображение, которое ставит в соответствие классу групп
отображение, которое ставит в соответствие классу групп  класс групп, состоящий из всех подгрупп всех
класс групп, состоящий из всех подгрупп всех  групп;
групп;
 когда
когда  является нормальной подгруппой
является нормальной подгруппой  группы;
группы;
 когда
когда  является гомоморфным образом некоторой
является гомоморфным образом некоторой  группы;
группы;
 когда
когда  является произведением конечного числа своих нормальных
является произведением конечного числа своих нормальных  подгрупп;
подгрупп;
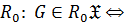 когда
когда  является прямым произведением своих нормальных
является прямым произведением своих нормальных  подгрупп;
подгрупп;
Определение 51. Класс групп  называется замкнутым относительно операции
называется замкнутым относительно операции 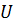 или
или  замкнутым, если
замкнутым, если  .
.
Определение 52. Класс групп  называется:
называется:
1) 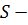 замкнутым или наследственным, если
замкнутым или наследственным, если  , то есть
, то есть  всегда
всегда  ;
;
2) 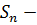 замкнутым или нормально наследственным, если
замкнутым или нормально наследственным, если  , то есть
, то есть 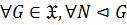 всегда
всегда  ;
;
3) 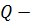 замкнутым или гомоморфом, если
замкнутым или гомоморфом, если 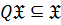 , то есть
, то есть  всегда
всегда  ;
;
4)  замкнутым, если
замкнутым, если  , то есть если
, то есть если  , то
, то  ;
;
5)  замкнутым, если
замкнутым, если  , то есть если
, то есть если 
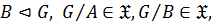 то
то  .
.
Лемма 5. Для произвольного класса групп  справедливо:
справедливо:
1)  , то есть
, то есть  ;
;
2)  , то есть
, то есть  ;
;
3)  , то есть
, то есть  ;
;
4) 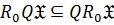 ;
;
5) 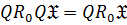 .
.
Теорема 9. Если класс  замкнут относительно произведений нормальных
замкнут относительно произведений нормальных  подгрупп, то каждая субнормальная
подгрупп, то каждая субнормальная  подгруппа группы
подгруппа группы  содержится в некоторой нормальной
содержится в некоторой нормальной  подгруппе группы
подгруппе группы  .
.
Следствие 1. Пусть класс  замкнут относительно произведений нормальных
замкнут относительно произведений нормальных  подгрупп. Если
подгрупп. Если  и
и  субнормальные
субнормальные  подгруппы группы
подгруппы группы  , то
, то  субнормальная
субнормальная  .
.
Глава 2. Классы Фиттинга конечных групп.
Классы Фиттинга и их основные свойства.
Определение 53. Класс групп  называется классом Фиттинга, если выполняются следующие условия:
называется классом Фиттинга, если выполняются следующие условия:
3) из  всегда следует, что
всегда следует, что  (1)
(1)
4) из 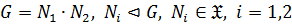 всегда следует, что
всегда следует, что
 . (2)
. (2)
Пример.Класс нильпотентных групп  является классом Фиттинга.
является классом Фиттинга.
1) Действительно, из  по лемме 4 1) следует, что
по лемме 4 1) следует, что  .
.
2) По лемме 4 2) из 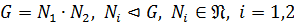 в силу выполнимости условий определения внутреннего произведения подгрупп группы следует, что
в силу выполнимости условий определения внутреннего произведения подгрупп группы следует, что  .
.
Лемма 6. Пусть  непустой класс Фиттинга. Тогда для любой группы
непустой класс Фиттинга. Тогда для любой группы  :
:
1)  ;
;
2) 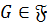 тогда и только тогда, когда
тогда и только тогда, когда  ;
;
3) 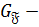 наибольшая нормальная
наибольшая нормальная  подгруппа группы
подгруппа группы  .
.
Лемма 7. Пересечение любой совокупности классов Фиттинга является классом Фиттинга.
Доказательство.
Пусть  классы Фиттинга,
классы Фиттинга,  . Покажем, что
. Покажем, что  класс Фиттинга.
класс Фиттинга.
1) Пусть  . Покажем, что
. Покажем, что 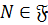 . Поскольку
. Поскольку 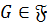 , а
, а  , то по определению операции пересечения получаем:
, то по определению операции пересечения получаем:  . Тогда из определения класса Фиттинга следует, что
. Тогда из определения класса Фиттинга следует, что 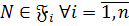 . Поэтому
. Поэтому 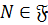 .
.
2) Пусть  . Покажем, что
. Покажем, что  . Так как
. Так как  , то
, то  . Поскольку
. Поскольку  классы Фиттинга, то
классы Фиттинга, то
 . А это означает, что
. А это означает, что 
 .
.
Определение 54. Пусть  непустой класс Фиттинга.
непустой класс Фиттинга.  радикалом группы
радикалом группы  называется произведение всех ее нормальных
называется произведение всех ее нормальных  подгрупп.
подгрупп.
Лемма 8. Пусть  класс Фиттинга,
класс Фиттинга,  группа и
группа и  . Тогда и только тогда
. Тогда и только тогда  , когда
, когда 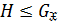 .
.
Доказательство.
Пусть  и
и  . По следствию 1 получаем, что
. По следствию 1 получаем, что 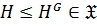 и
и
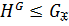 .
.
Обратно, пусть  и
и 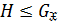 . Так как
. Так как  и выполняется требование (1), то
и выполняется требование (1), то  .
.
Лемма 9. Если  класс Фиттинга и
класс Фиттинга и  , то
, то  .
.
Доказательство.
Так как  и
и  , то
, то 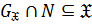 . Поскольку
. Поскольку  , то
, то 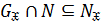 . Обратно,
. Обратно,  , поэтому
, поэтому 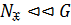 и по лемме 8 подгруппа
и по лемме 8 подгруппа  . Итак,
. Итак,  .
.
Дата добавления: 2018-02-18; просмотров: 762; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
