Свойства неопределенного интеграла.
1. 
;
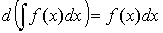2. 
;
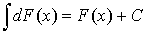3. 
;
4. 
.
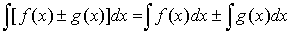(35) Таблица интегралов
(36) Интегрирование по частям
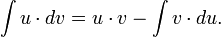
(38)Определённый интеграл. Пусть f(x) определена на [a;b]. Разобьём [a;b] на части с несколькими произвольными точками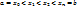 
Тогда говорят, что произведено разбиение R отрезка [a;b]. Определённым интегралом от функции f(x) на отрезке [a;b] назыв. предел интегральных сумм при стремлении ранга разбиения к нулю
Если существует указанный предел, то функция f(x) называется интегрируемой на [a;b].
Св-ва:
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.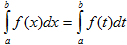 
, где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.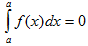 
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.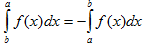 
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.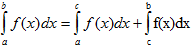 
V. Постоянный множитель можно выносить за знак определенного интеграла.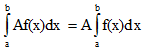 
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.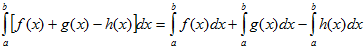 
(39) Теорема о среднем
Пусть f(x) непрерывна на [a;b] тогда сущ. 
такая что 
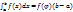
(40) Геом. приложения опред. интеграла(S,V, l)
; 
; 
|
|
|
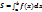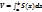
(41) Несобств. инт. 1 рода, опред. и св-ва.
Пусть f(x) опред. (a;∞) и сущ.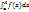 
при любом А>a. Обозначим 
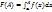, тогда, если сущ. 
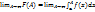, конечный предел, то он назыв.несобств. инт. 1 рода 
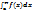.В противн. случае, если не сущ. конечного пред., то инт. назыв. расходящимся, если сущ. – сходящимся.
(42) Несобств. инт. 2 рода, опред. и св-ва.
Пусть f(x) интергрир. на (a;A), при любом A>a, f(x) неогранич. в лев. полуокрестн. точки b. 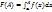, если сущ. 
, то он назыв.несобств. инт. 2 рода 
(43) Исслед. несоб. инт. на сходимость.
Очень часто нужно узнать сходится интеграл или расходится, не вычисляя его. Для этого используются признаки сходимости, которые мы сформулируем сразу для несобственных интегралов обоих типов, полагая, что b может быть бесконечным или конечной особой точкой. Признаки сходимости: Если интеграл 
сходится, то интеграл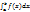 
тоже сходится. В этом случае интеграл 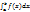называют абсолютно сходящимся. Пусть 
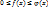. Тогда, если интеграл 
сходится, то интеграл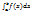 
тоже сходится и, если интеграл 
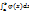расходится, то интеграл 
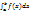тоже расходится. 3. Пусть b есть особая точка функции f(x). Если при x→b существует предел 
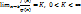то интегралы 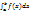и 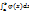сходятся или расходятся одновременно.
1) 
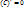
2) (хn)=n•хn-1
3) (ex)'=ex
|
|
|
4) (aх)'=aхInа
5) 
6) (sinx)'=cosx.
7) (cosх)'=-sinx
8) 
9) 
10) 
11) 
12) 
13) 
1)
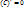
2) (хn)=n•хn-1
3) (ex)'=ex
4) (aх)'=aхInа
5)
6) (sinx)'=cosx.
7) (cosх)'=-sinx
8)
9)
10)
11)
12)
13)
Дата добавления: 2018-02-15; просмотров: 486; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!