Ортогональность системы сферических функций
Докажем, что сферические функции, соответствующие различным значениям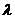 
, ортогональны на поверхности сферы 
. Пусть 
и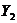 
удовлетворяют уравнениям
,
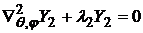, (19)
где 
.
Нетрудно видеть что имеет место формула
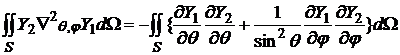, (20)
которая легко получается интегрирование по частям ( 
). На поверхности сферы:
,
,
Так что используя
и формулу (20) можно записать в виде
.
Меняя местами в формуле (20) функции 
и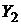 
, а также вычитая полученную формулу из формулы (20), будем иметь
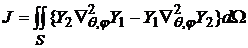(21)
Формулы (20) и (21) являются формулами Грина для операторов сферических функций. Из формулы (21) легко следует ортогональность и 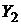. В самом деле, пользуясь уравнениями (19), получим из формулы (21)
,
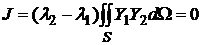откуда при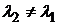 
получим, что
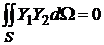, или
.
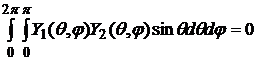Тем самым доказана ортогональность сферических функций, соответствующих разным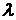 
.
Глава 2. Полиномы Чебышева- Эрмита и Чебышева- Лагерра
Полиномы Чебышева- Эрмита
Дифференциальная формула
Полиномы Чебышева-Эрмита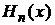 
определим по аналогии с полиномами Лежандра при помощи производящей функции 
:
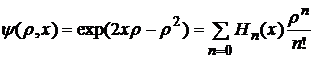. (1)
Отсюда в силу теоремы Коши следует
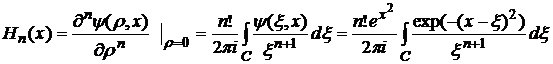, (2)
где С – замкнутый контур в плоскости комплексного переменного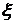 
, охватывающий точку 
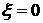. Вводя новую переменную интегрирования
,
,
,
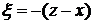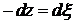преобразуем (2) к виду
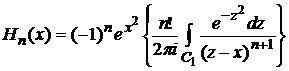(3)
Где С1- контур, охватывающий точку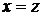 
. В силу теоремы Коши выражение в фигурных скобках равно 
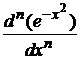. В результате получаем из (3) дифференциальную формулу 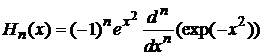(4)
|
|
|
,
. (4)
Эта формула показывает, что 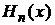есть полином степени n, причем
(5)
Рекуррентные формулы
Дифференцируя производящую функцию
,
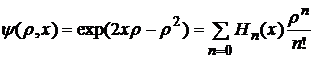по 
и 
, находим
,
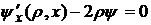. (6)
,
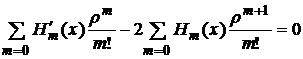Меняем коэффициенты
.
Используем первую формулу из (6) и найдем
(7)
,
.
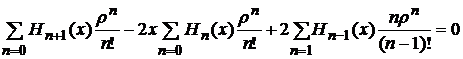Получаем рекуррентную формулу
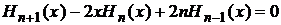(8)
Уравнение Чебышева- Эрмита
Используя соотношение (7) заменяем в (8) последнее слагаемое и дифференцируем:
,
.
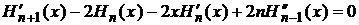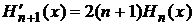
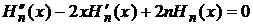Мы получаем уравнение Чебышева- Эрмита:
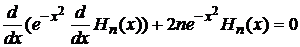(9)
Отсюда видно что полином Чебышева-Эрмита является собственной функции соотношения для собственного значения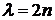 
и сводится к задаче Штурма-Лиувиля.
Найти те значения 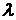, при которых уравнение Чебышева- Эрмита
, 
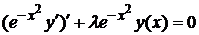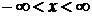, (11)
имеет нетривиальное решение, возрастающее при 
, не быстрее чем конечная степень .
Решение этой задачи можно было бы искать в виде степенного ряда
.
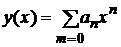Подставив этот ряд в уравнение (10), получим для коэффициентов рекуррентную формулу
.
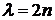(12)
|
|
|
Из формулы (12) видно, что при 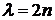все коэффициенты 
обращаются в 0 для 
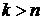и ряд обрывается. Только при требовании 
может быть выполнено условие на бесконечности. Полученные полиномы будут определены с точностью до постоянного множителя 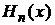. Выбирая 
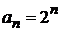, получаем полиномы .
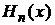Упражнения
1. Используя дифференциальную формулу (4) (Глава 2) получить полиномы Чебышева-Эрмита для n=0,1,2,3,4.
Ответ:
; 
; 
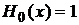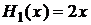и т. д.
2. Используя рекуррентные формулы (7) и (8) (Глава 2) найти полиномы Чебышева-Эрмита для n=0,1...7.
Ответ:
,
,
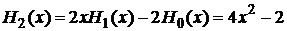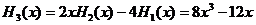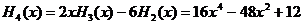
3. Используя рекуррентную формулу для коэффициентов (12) (Глава 2) найти полиномы Чебышева-Эрмита для n=0,1...4.
4. Получить функции Чебышева-Эрмита для n=0,1,2 и найти их норму.
Дата добавления: 2018-02-15; просмотров: 524; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!