Определение положения нейтральной оси. Напомним, что нейтральная ось – это геометрическое место точек поперечного сечения, где нормальные напряжения равны нулю.
При косом изгибе
Напомним, что нейтральная ось – это геометрическое место точек поперечного сечения, где нормальные напряжения равны нулю.
Тогда, используя уравнение (14.4), получим уравнение нейтральной оси
 (14.10)
(14.10)
где  и
и  - координаты точки
- координаты точки  , принадлежащей нейтральной оси (см. рис. 14.2). Преобразуя уравнение (14.8), получим
, принадлежащей нейтральной оси (см. рис. 14.2). Преобразуя уравнение (14.8), получим
 и, используя (14.2) –
и, используя (14.2) –

так как 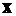 - постоянная величина для конкретного сечения, а
- постоянная величина для конкретного сечения, а  (по рис. 14.2), поэтому
(по рис. 14.2), поэтому  . (14.11)
. (14.11)
 Рис. 14.2 К примеру расчета
величины и направления полного прогиба при косом изгибе
Рис. 14.2 К примеру расчета
величины и направления полного прогиба при косом изгибе
|
где 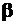 - угол наклона нейтральной оси к оси - угол наклона нейтральной оси к оси  . Косого изгиба не будет, если . Косого изгиба не будет, если 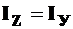 , то есть для круглого и квадратного поперечных сечений.
В этом примере:
Учитывая знаки напряжений от , то есть для круглого и квадратного поперечных сечений.
В этом примере:
Учитывая знаки напряжений от 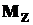 и и 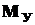 (растяжение или сжатие), можно подсчитать напряжения в опасных точках сечения (1…4) и построить соответствующие эпюры. (растяжение или сжатие), можно подсчитать напряжения в опасных точках сечения (1…4) и построить соответствующие эпюры.
|
Определение величины и направления полного
Прогиба при косом изгибе
В соответствии с чертежом (рис. 14.2) полный прогиб при косом изгибе может быть определен, если известны составляющие 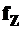 и
и  , по формуле
, по формуле
 . (14.12)
. (14.12)
На примере консольной балки может быть определено и направление полного прогиба - угол  . Так,
. Так,
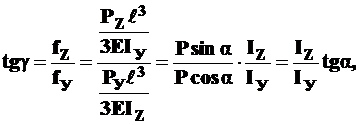
то есть  (14.13)
(14.13)
Как видно из формул (14.12) и (14.13), углы  и
и  равны между собой, то есть направление полного прогиба перпендикулярно нейтральной оси и не совпадает с направлением силы
равны между собой, то есть направление полного прогиба перпендикулярно нейтральной оси и не совпадает с направлением силы 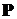 , поэтому рассмотренный вид изгиба и назван косым.
, поэтому рассмотренный вид изгиба и назван косым.
Потенциальная энергия при косом изгибе
Потенциальная энергия может быть также подсчитана с использованием принципа независимости действия сил, то есть
 (14.14)
(14.14)
где 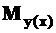 и
и 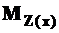 - уравнения изгибающих моментов на силовых участках стержня в вертикальной и горизонтальной плоскостях.
- уравнения изгибающих моментов на силовых участках стержня в вертикальной и горизонтальной плоскостях.
Лекция 15
Внецентренное сжатие (растяжение).
Нормальные напряжения, расчет на прочность
Теоретические расчеты, которые будут сделаны ниже, относятся к коротким массивным стержням, то есть к таким стержням, которым не угрожает потеря устойчивости под действием продольных сжимающих сил.
 Рис. 15.1 К расчету величины напряжений и положения нейтральной
оси при внецентренном сжатии
Рис. 15.1 К расчету величины напряжений и положения нейтральной
оси при внецентренном сжатии
| Рассмотрим такой стержень, нагруженный сжимающей силой 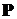 , приложенной в точке , приложенной в точке 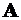 , которая называется полюсом. Координаты точки , которая называется полюсом. Координаты точки 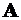 называются эксцентриситетами - называются эксцентриситетами -  ; ;  , то есть сила , то есть сила 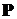 приложена вне центра тяжести сечения (рис. 15.1).
Перенесем в два этапа силу приложена вне центра тяжести сечения (рис. 15.1).
Перенесем в два этапа силу 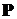 в центр тяжести сечения. Вначале перенесем силу в центр тяжести сечения. Вначале перенесем силу 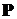 параллельно оси параллельно оси  на ось на ось 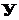 . При этом, в соответствии с правилами теоретической механики, образуется пара сил с плечом . При этом, в соответствии с правилами теоретической механики, образуется пара сил с плечом  , то есть , то есть   . Затем перенесем силу . Затем перенесем силу 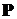 с оси с оси  в центр в центр
|
тяжести сечения. При этом образуется пара сил с плечом  , то есть
, то есть 
 . Таким образом, налицо три внутренних силовых фактора – моменты
. Таким образом, налицо три внутренних силовых фактора – моменты 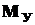 и
и 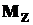 и сжимающая (или растягивающая) сила
и сжимающая (или растягивающая) сила 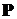 , приложенная в центре тяжести сечения. Воспользовавшись снова принципом независимости действия сил, напишем уравнение нормальных напряжений для произвольной точки сечения при внецентренном растяжении или сжатии
, приложенная в центре тяжести сечения. Воспользовавшись снова принципом независимости действия сил, напишем уравнение нормальных напряжений для произвольной точки сечения при внецентренном растяжении или сжатии
 . (15.1)
. (15.1)
Знак перед слагаемыми правой части уравнения ставится в зависимости оттого, что вызывает соответствующий силовой фактор в исследуемой точке сечения – растяжение или сжатие.
Уравнение (15.1) можно преобразовать так:
 (15.2)
(15.2)
где  и
и  - радиусы инерции поперечного сечения.
- радиусы инерции поперечного сечения.
Критерий прочности для внецентренного растяжения-сжатия элемента с сечением, имеющим оси симметрии, может быть записан следующим образом
 . (15.3)
. (15.3)
Порядок подбора сечения аналогичен порядку, изложенному для случая косого изгиба (см. предыдущую лекцию).
Фактические напряжения проверяются по формуле
 . (15.4)
. (15.4)
Дата добавления: 2018-02-15; просмотров: 2274; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
