Задание 3.2. Решить системы, находя фундаментальную систему решений.
Системы дифференциальных уравнений
3.1. Интегрирование систем линейных дифференциальных уравнений с
постоянными коэффициентами сведением к одному
дифференциальному уравнению
Многие системы дифференциальных уравнений, как однородные, так и неоднородные, могут быть сведены к одному уравнению относительно одной неизвестной функции. Покажем метод на примерах.
Пример 3.1.Решить систему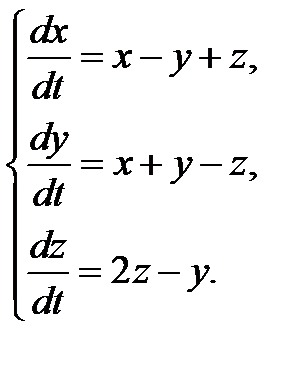 
Решение. 1) Дифференцируя по t первое уравнение и используя второе и третье уравнения для замены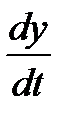 
и 
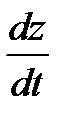, находим
.
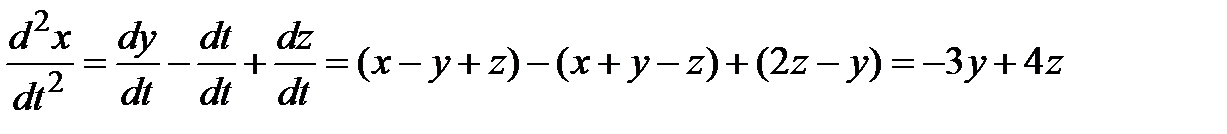Полученное уравнение дифференцируем по 
еще раз
.
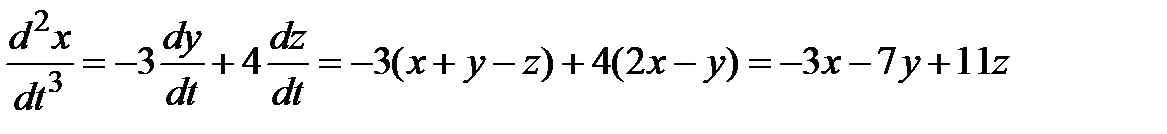1) Составляем систему
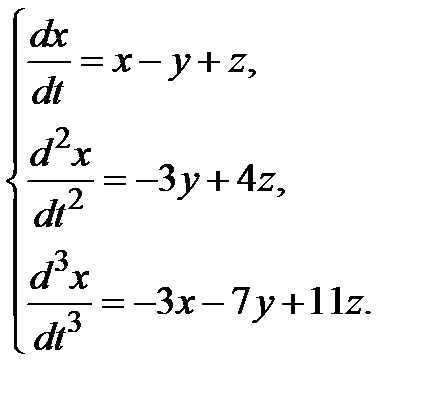
Из первых двух уравнений системы выразим переменные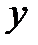 
и 
через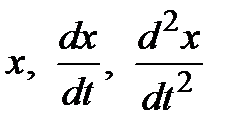 
:
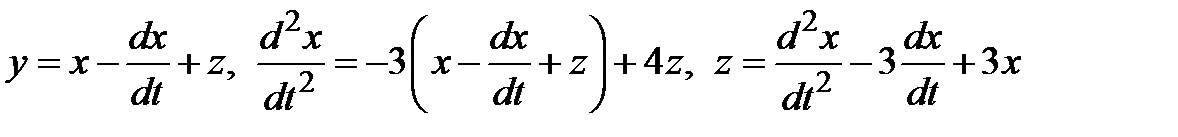. (3.1)
Подставим найденные выражения для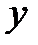 
и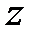 
в третье уравнение системы
.
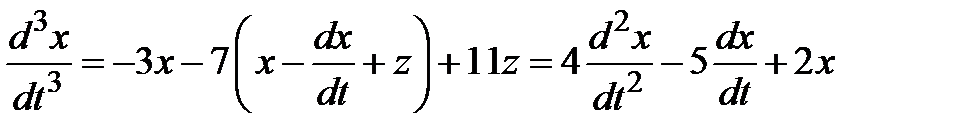Итак, для нахождения функции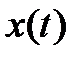 
получили дифференциальное уравнение третьего порядка с постоянными коэффициентами
.
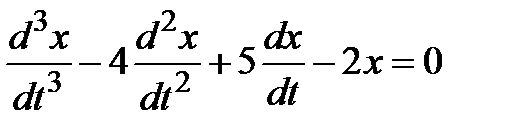2) Интегрируем последнее уравнение стандартным методом: составляем характеристическое уравнение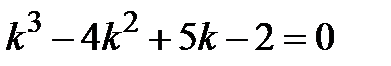 
, находим его корни 
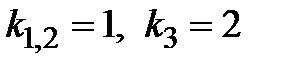и строим общее решение в виде линейной комбинации экспонент, учитывая кратность одного из корней: 
.
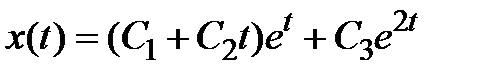3) Далее, чтобы найти две оставшиеся функци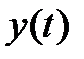и 
и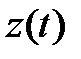 
, дифференцируем дважды полученную функцию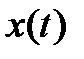 
.
Используя связи (3.1) между функциями системы, восстанавливаем оставшиеся неизвестные
.
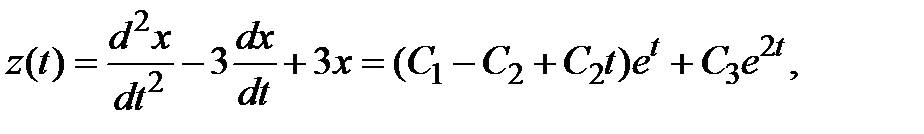
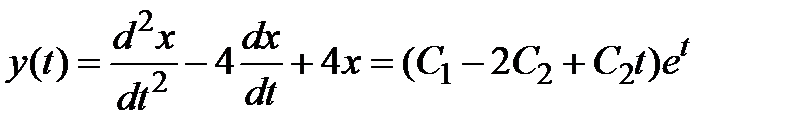Ответ. 
, 
, 
.
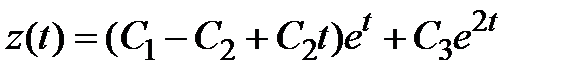Может оказаться, что все известные функции кроме одной исключаются из системы третьего порядка уже при однократном дифференцировании. В таком случае, порядок дифференциального уравнения для ее нахождения будет меньше, чем число неизвестных функций в исходной системе.
|
|
|
Пример 3.2. Проинтегрировать систему
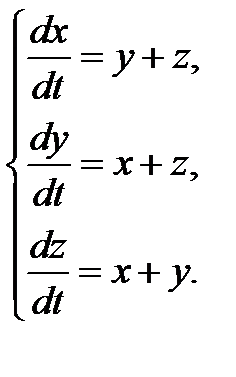(3.2)
Решение. 1) Дифференцируя по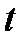 
первое уравнение, находим
.
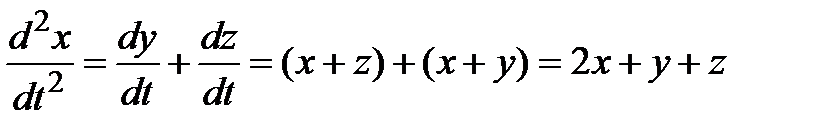Исключая переменные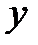 
и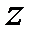 
из уравнений
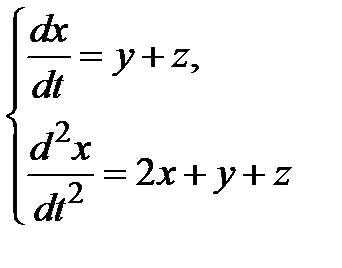
будем иметь уравнение второго порядка относительно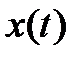 
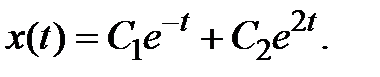(3.3)
2) Из первого уравнения системы (3.2) имеем
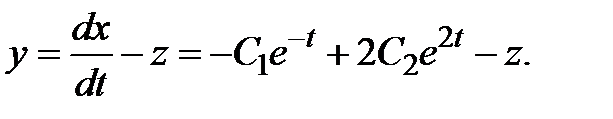(3.4)
Подставляя в третье уравнение системы (3.2) найденные выражения (3.3) и (3.4) для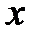 
и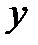 
, получим дифференциальное уравнение первого порядка для определения функции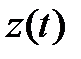 
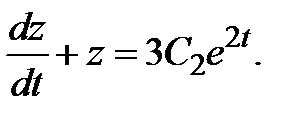
Интегрируя это неоднородное уравнение с постоянными коэффициентами первого порядка, найдем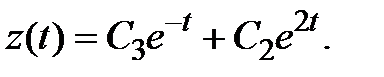 
Используя (3.4), находим функцию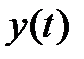 
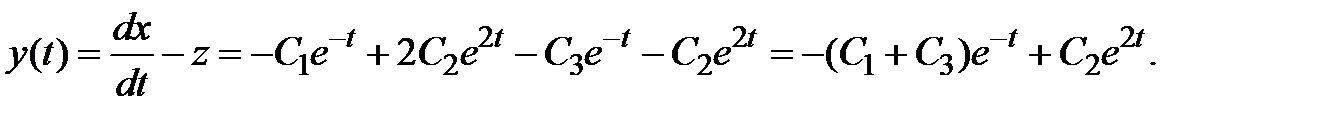
Ответ. 
, 
, 
.
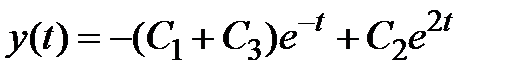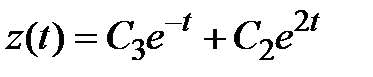Задание 3.1. Решить однородные системы сведением к одному дифференциальному уравнению.
|
|
|
3.1.1. 
3.1.2.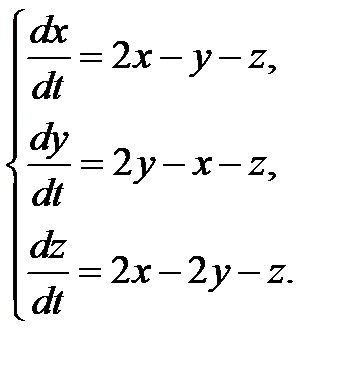 
3.1.3.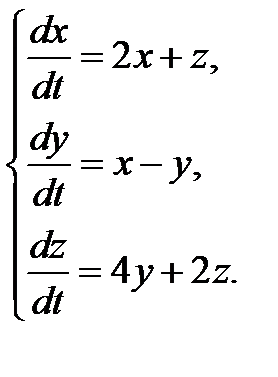 
3.1.4. 
3.1.5.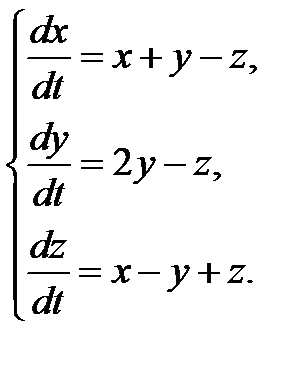 
3.1.6.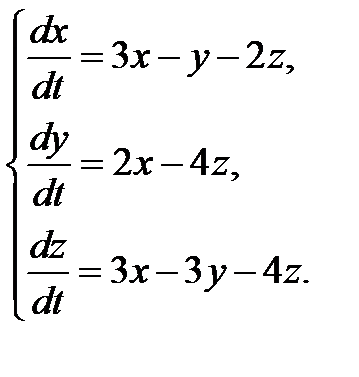 
3.1.7.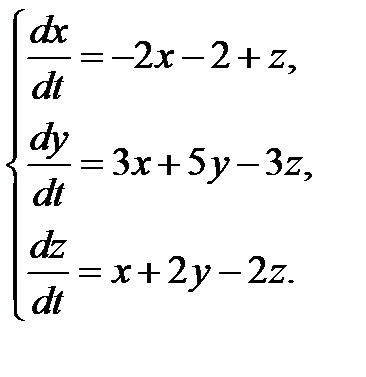 
3.1.8. 
3.1.9. 
3.1.10. 
3.1.11. 
3.1.12.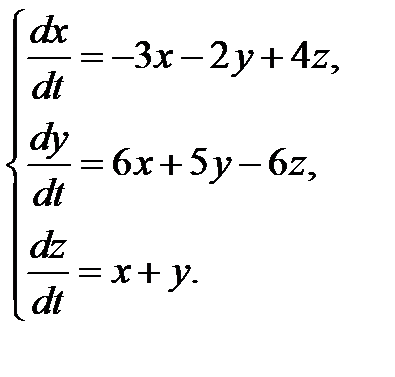 
3.1.13.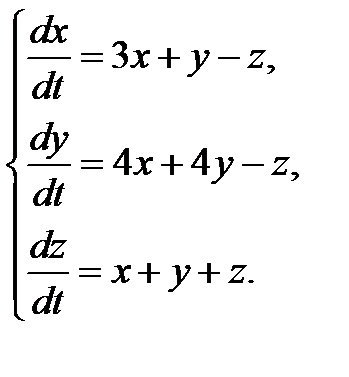 
3.1.14.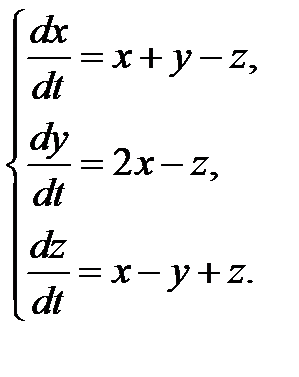 
3.1.15.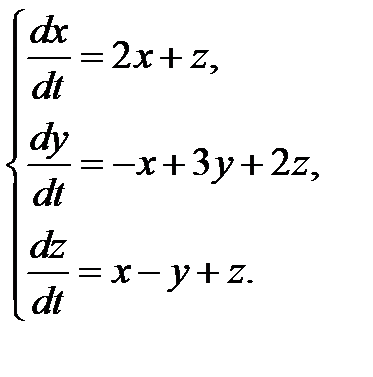 
3.1.16.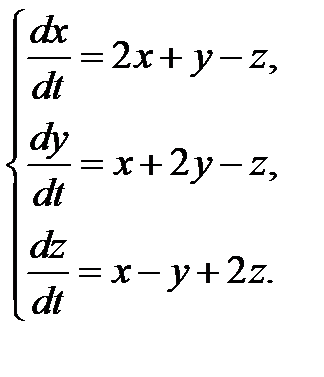 
3.1.17. 
3.1.18.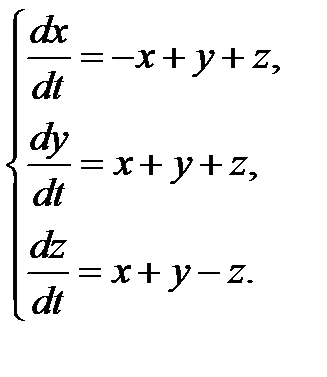 
3.1.19.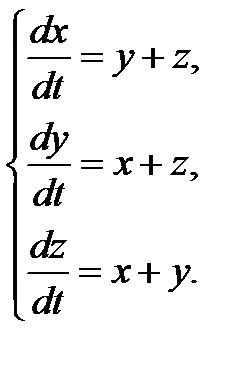 
3.1.20.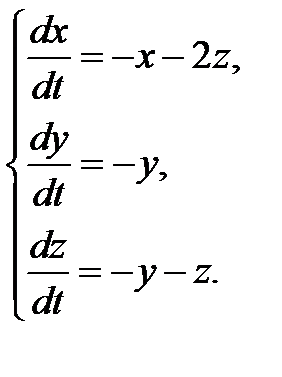 
3.1.21.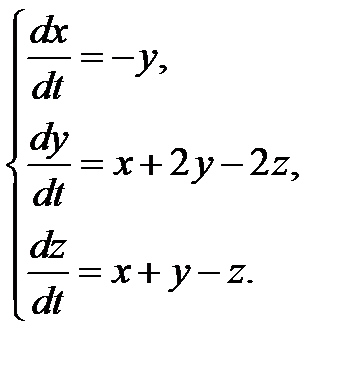 
3.1.22.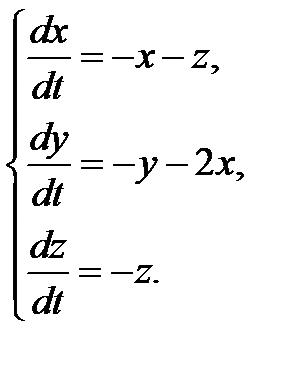 
3.1.23.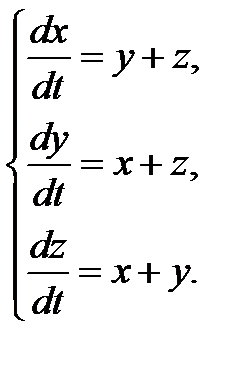 
3.1.24.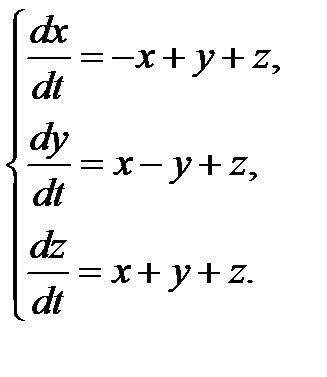 
3.1.25.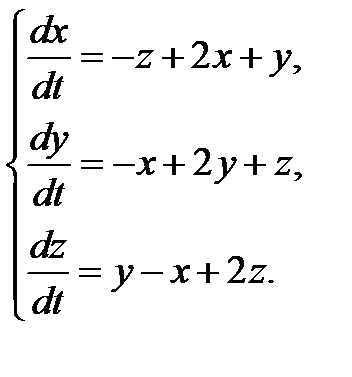 
3.1.26.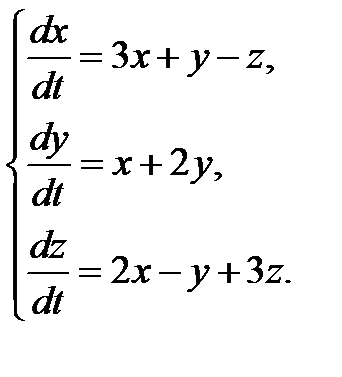 
3.1.27.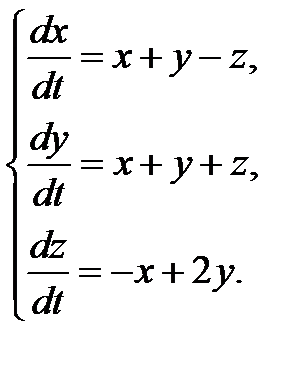 
3.1.28. 
3.1.29.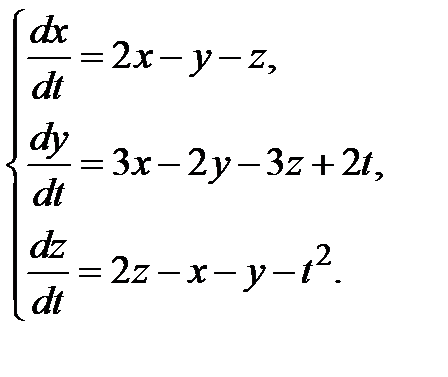 
3.1.30.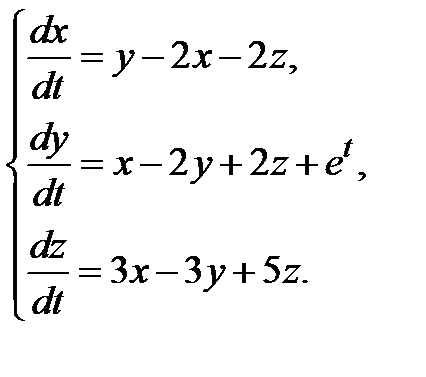 
3.2. Решение систем линейных однородных дифференциальных уравнений с постоянными коэффициентами с помощью нахождения
фундаментальной системы решений
Общее решение системы линейных однородных дифференциальных уравнений может быть найдено как линейная комбинация фундаментальных решений системы. В случае систем с постоянными коэффициентами для нахождения фундаментальных решений могут быть использованы методы линейной алгебры.
Пример 3.3. Решить систему
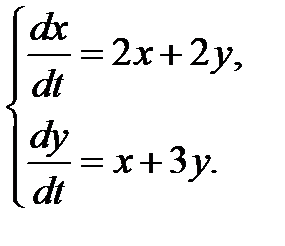(3.5)
|
|
|
Решение. 1) Перепишем систему в матричном виде
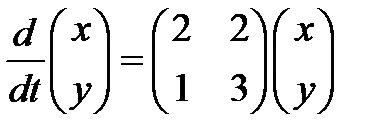. (3.6)
2) Будем искать фундаментальное решение системы в виде вектора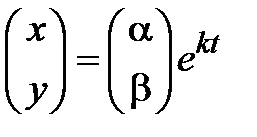 
. Подставляя функции 
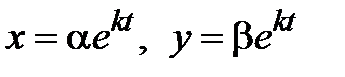в (3.6) и сокращая на 
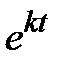, получим
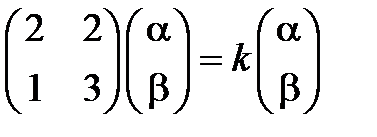
или
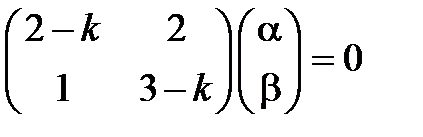, (3.7)
то есть число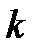 
должно быть собственным числом матрицы 
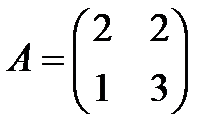, а вектор 
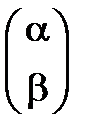соответствующим собственным вектором.
3) Из курса линейной алгебры известно, что система (3.7) имеет нетривиальное решение, если ее определитель равен нулю
,
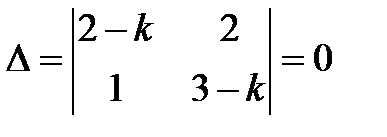то есть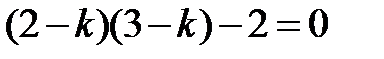 
. Отсюда находим собственные значения 
.
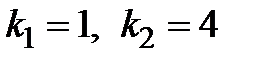4) Найдем соответствующие собственные векторы. Подставляя в (3.7) первое значение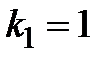 
, получим систему для нахождения первого собственного вектора
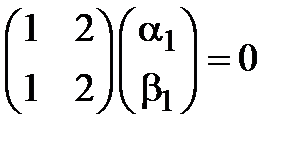
или
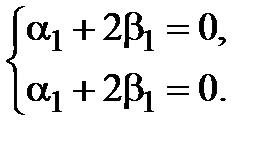
Отсюда получаем связь между неизвестными 
. Нам достаточно выбрать одно нетривиальное решение. Полагая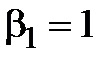 
, тогда 
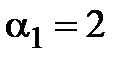, то есть вектор 
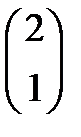является собственным для собственного значения 
, а вектор функции 
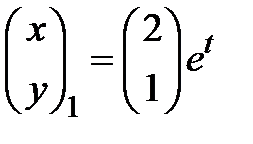фундаментальным решением заданной системы дифференциальных уравнений (3.5). Аналогично, при подстановке второго корня 
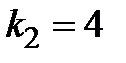в (3.7) имеем матричное уравнение для второго собственного вектора 
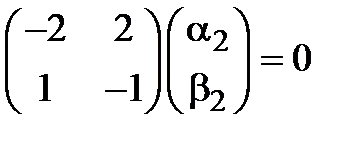. Откуда получаем связь между его компонентами 
. Таким образом, имеем второе фундаментальное решение
|
|
|
.
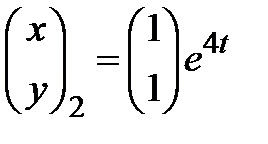5) Общее решение системы (3.5) строится как линейная комбинация двух полученных фундаментальных решений
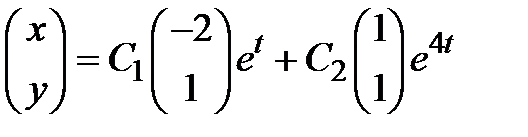
или в координатном виде
.
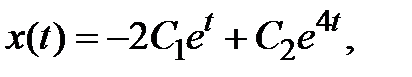
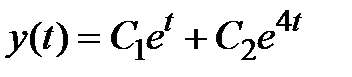Ответ. .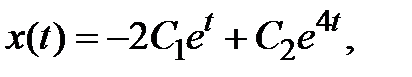
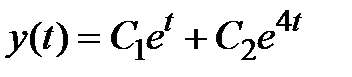Задание 3.2. Решить системы, находя фундаментальную систему решений.
3.2.1.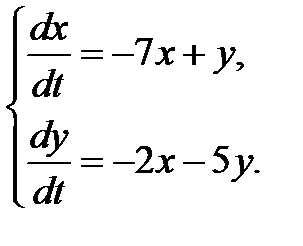 
3.2.2.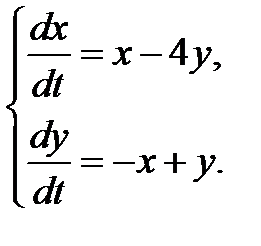 
3.2.3.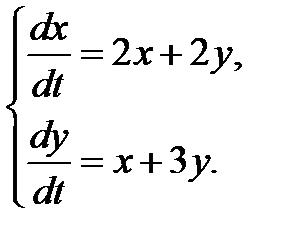 
3.2.4. 
3.2.5.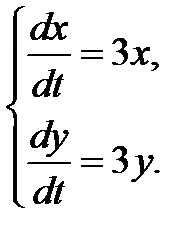 
3.2.6.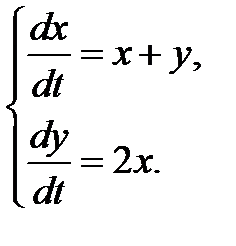 
3.2.7.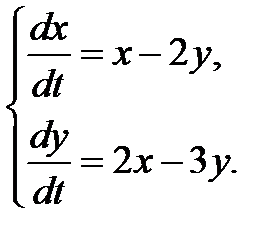 
3.2.8. 
3.2.9.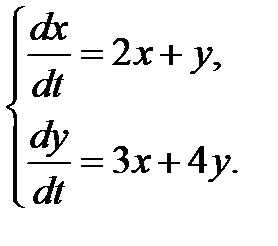 
3.2.10. 
3.2.11.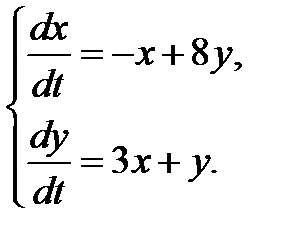 
3.2.12. 
3.2.13.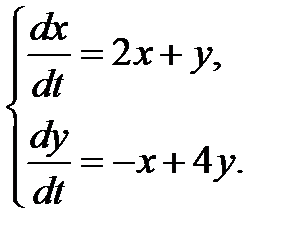 
3.2.14.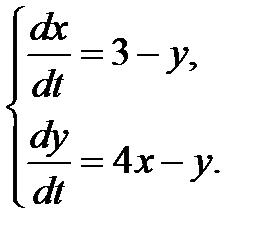 
3.2.15.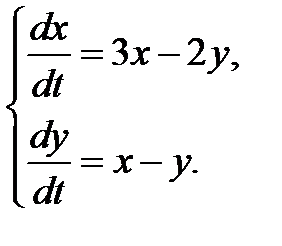 
3.2.16.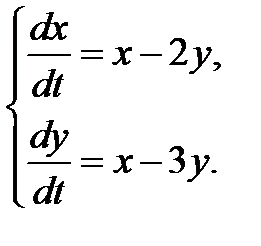 
3.2.17.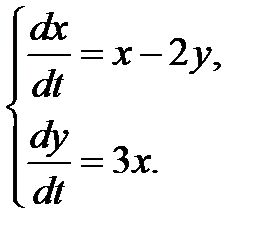 
3.2.18.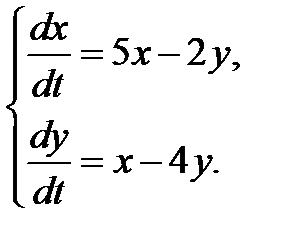 
3.2.19.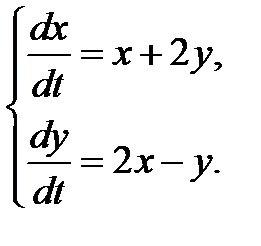 
3.2.20. 
3.2.21.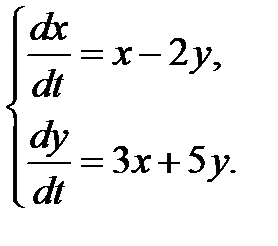 
3.2.22. 
3.2.23. 
3.2.24.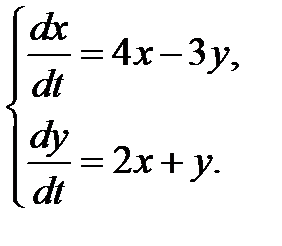 
3.2.25.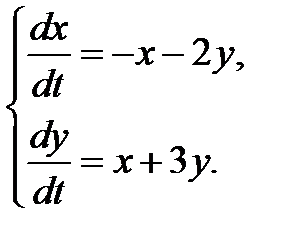 
3.2.26.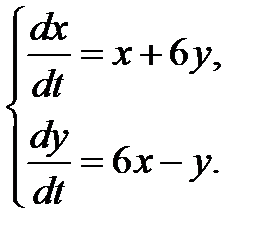 
3.2.27.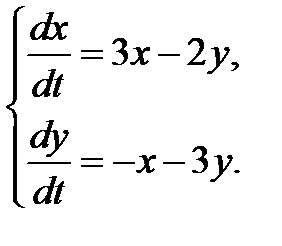 
3.2.28.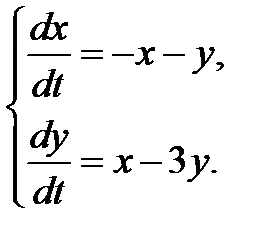 
3.2.29. 
3.2.30. 
3.3. Линейные неоднородные системы дифференциальных уравнений с
постоянными коэффициентами
Пусть задана неоднородная система линейных дифференциальных уравнений. Если найдена фундаментальная система решений соответствующей однородной системы, то решение неоднородной системы может быть найдено методом вариации произвольных постоянных.
Пример 3.4. Решить линейную неоднородную систему двух уравнений методом вариации постоянных
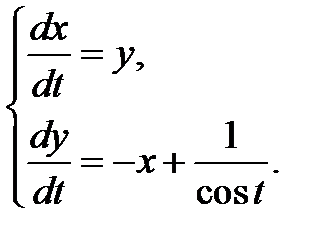(3.8)
Решение. 1) Найдем сначала общее решение соответствующей однородной системы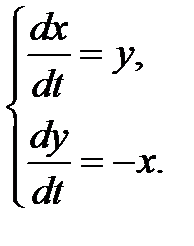 
Составляем характеристическое уравнение 
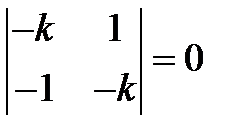или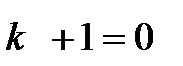 
, находим его корни 
.
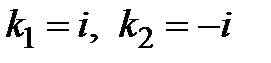2) В случае комплексно-сопряженных корней для системы с действительными коэффициентами, два линейно-независимых решения находят как действительную и мнимую части комплексного вектора, отвечающего одному из комплексных корней. Запишем матричное уравнение (см.3.7) для собственного числа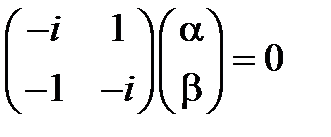 
. Откуда получаем связь между его компонентами 
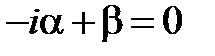и комплексное фундаментальное решение в векторном виде 
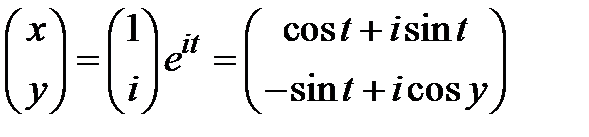. Тогда два действительных фундаментальных решения 
, 
.
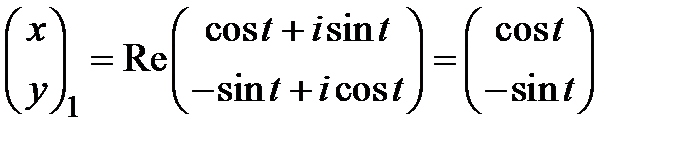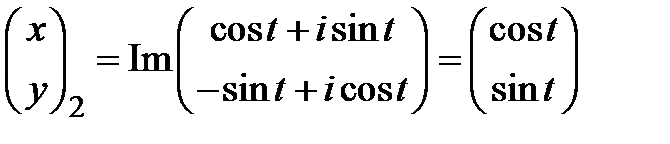3) Следовательно, общее решение однородной системы
.
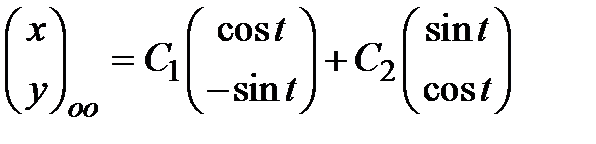4) Общее решение неоднородной системы ищем методом вариации произвольных постоянных, то есть рассматриваем параметры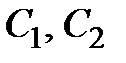 
как функции переменной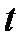 
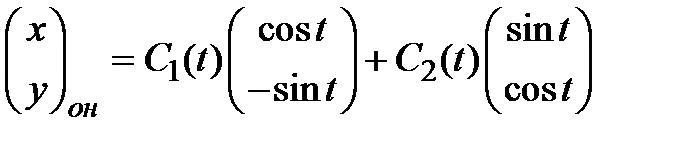. (3.9)
Подставляя вектор (3.9) в (3.8), получим для нахождения функций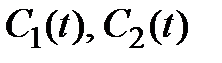 
систему
.
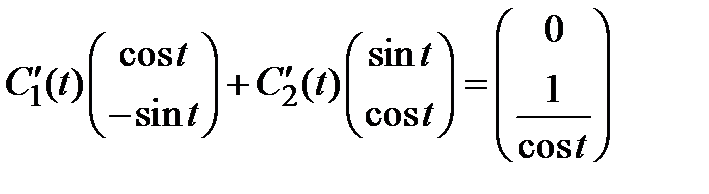Эта система всегда разрешима, т.к. ее определитель есть определитель Вронского для двух линейно-независимых векторных решений и, следовательно, не равен нулю ни при каком значении независимой переменной.
5) Решаем систему по правилу Крамера
,
,
,
.
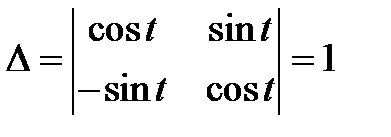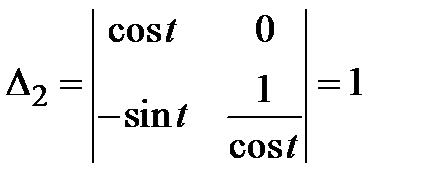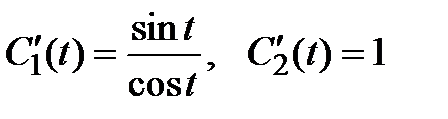Интегрируя, получаем
.
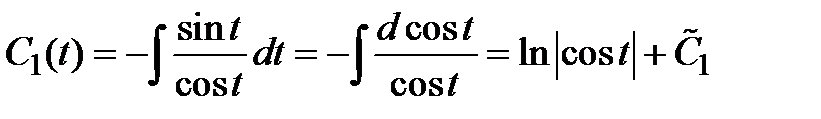Таким образом,
,
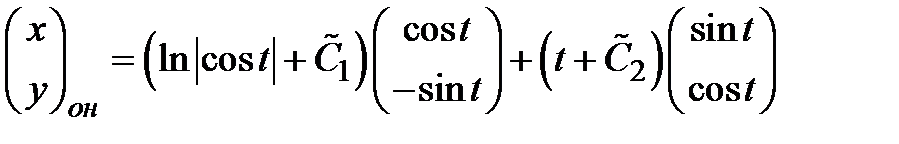где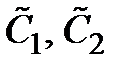 
- произвольные постоянные.
Ответ.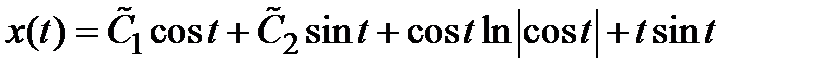 
, 
.
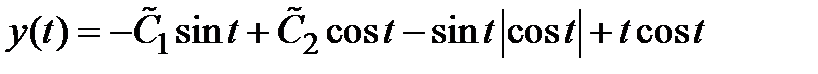Система неоднородных уравнений может быть также решена сведением к одному дифференциальному уравнению относительно неизвестной функции. Если в неоднородной системе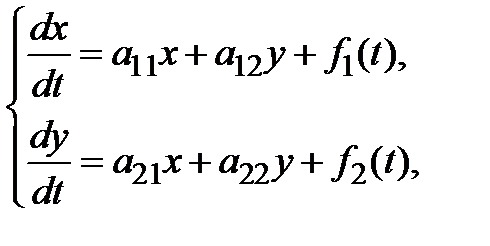 
вектор функция 
имеет вид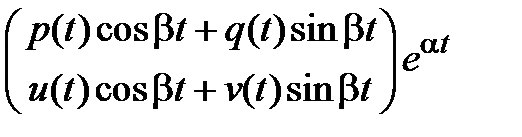 
, то может быть использован метод неопределенных коэффициентов для нахождения частного решения системы.
Задание 3.3. Решить системы.
3.3.1.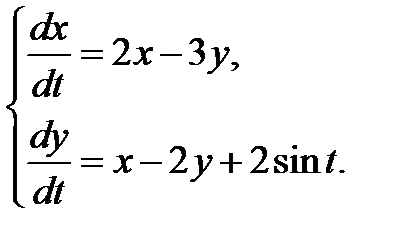 
3.3.2.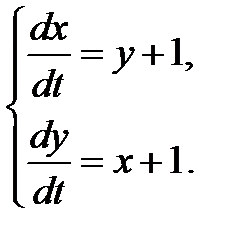 
3.3.3.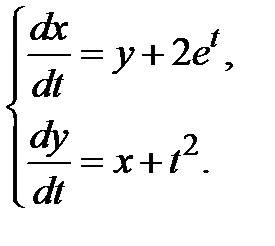 
3.3.4.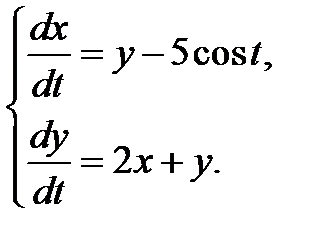 
3.3.5.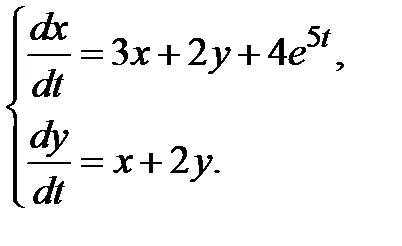 
3.3.6.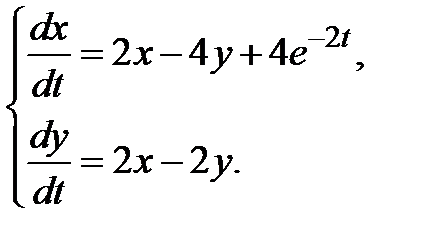 
3.3.7.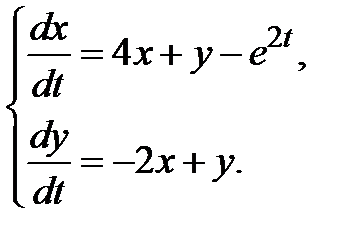 
3.3.8.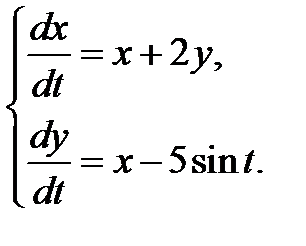 
3.3.9.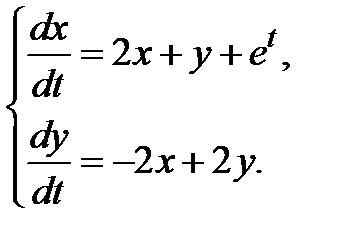 
3.3.10.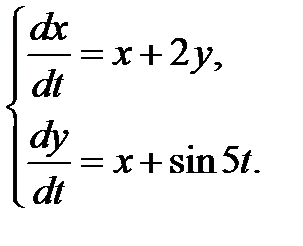 
3.3.11.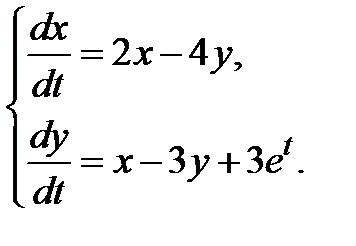 
3.3.12.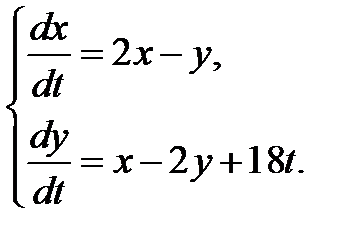 
3.3.13.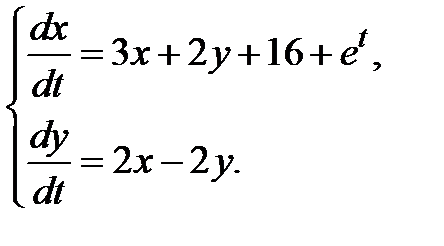 
3.3.14. 
3.3.15.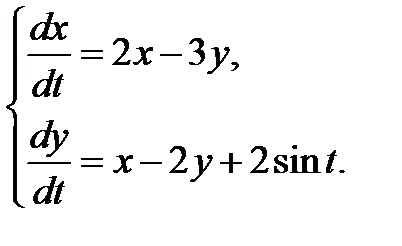 
3.3.16.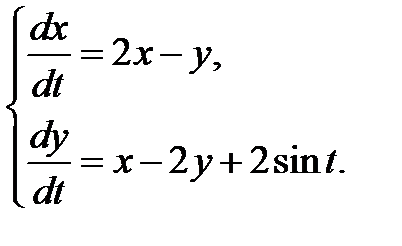 
3.3.17.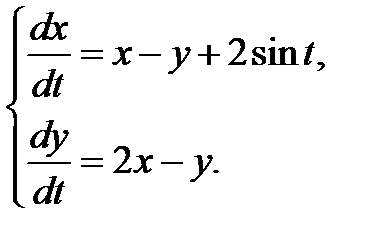 
3.3.18.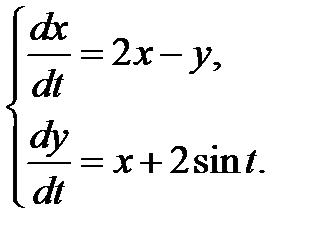 
3.3.19.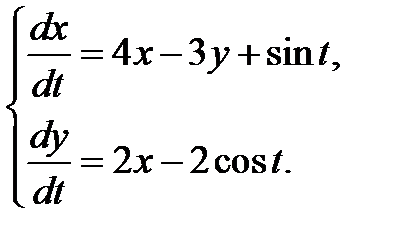 
3.3.20. 
3.3.21.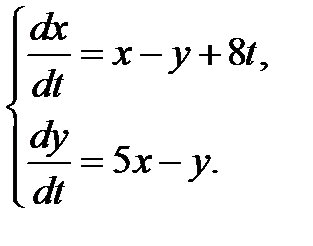 
3.3.22.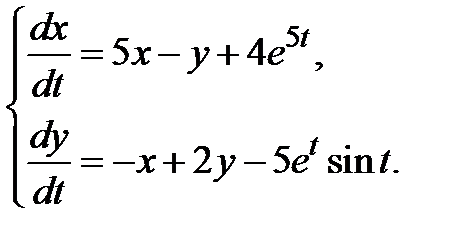 
3.3.23.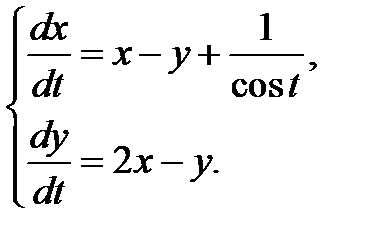 
3.3.24.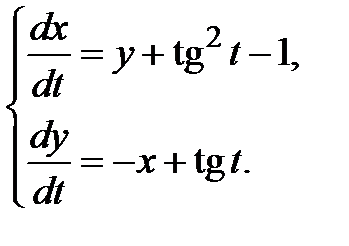 
3.3.25.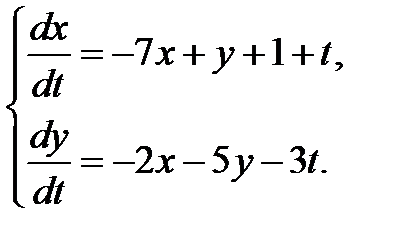 
3.3.26.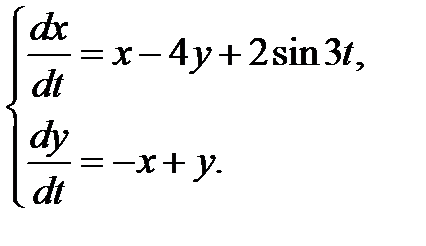 
3.3.27.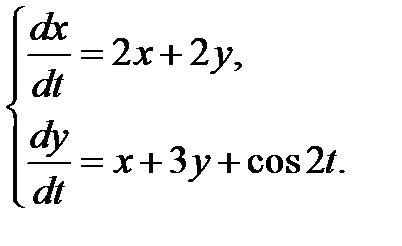 
3.3.28. 
3.3.29.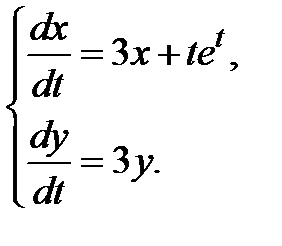 
3.3.30. 
3.4. Исследование на устойчивость однородной линейной системы
дифференциальных уравнений
При использовании дифференциальных уравнений или систем дифференциальных уравнений важным является наличие устойчивости решений: малые изменения начальных условий должны вызывать малые изменения решений. Для дифференциальных уравнений и систем первого порядка исследование на устойчивость решения сводится к исследованию на устойчивость тривиального решения (точки покоя). В случае однородных линейных систем с постоянными коэффициентами устойчивость точки покоя и ее тип определяется значениями корней характеристического уравнения.
Пример 3.5. Исследовать на устойчивость и определить тип точки покоя системы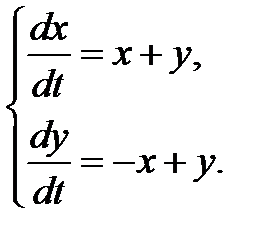 
Решение. 1) Составляем характеристическое уравнение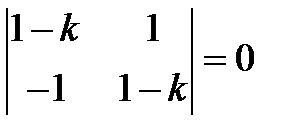 
.
2) Находим его корни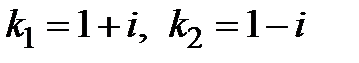 
.
3) Вычисляем действительные части корней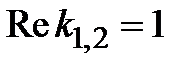 
.
4) Так как действительная часть больше нуля, то точка покоя является неустойчивой, ее тип – неустойчивый фокус.
Ответ. Неустойчива, неустойчивый фокус.
Дата добавления: 2018-02-15; просмотров: 893; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!