Задачи для контрольной работы. Найти наименьшее и наибольшее значения функции на отрезке .
Найти наименьшее и наибольшее значения функции 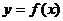 на отрезке
на отрезке  .
.
1. 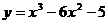 ,
,  . 14.
. 14. 
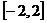 .
.
2. 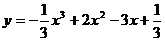 ,
, 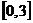 . 15.
. 15. 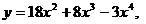
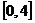 .
.
3. 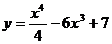 ,
, 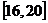 . 16.
. 16. 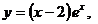
 .
.
4. 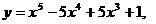
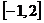 . 17.
. 17. 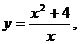
 .
.
5.  ,
, 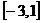 . 18.
. 18. 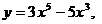
 .
.
6. 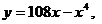
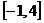 . 19.
. 19. 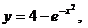
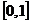 .
.
7. 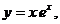
 . 20.
. 20. 
 .
.
8. 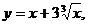
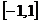 . 21.
. 21. 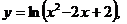
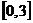 .
.
9. 
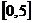 . 22.
. 22. 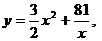
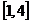 .
.
10. 
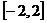 . 23.
. 23. 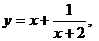
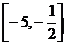 .
.
11. 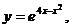
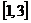 . 24.
. 24. 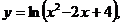
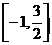 .
.
12. 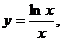
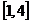 . 25.
. 25. 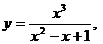
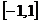 .
.
13. 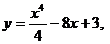
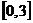 .
.
Дифференциальное исчисление функций нескольких переменных
2.1. Частные производные.
2.1.1.Вычисление частных производных функции двух переменных.Пусть функция двух переменных задана в некоторой области 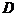 координатной плоскости. Если зафиксировать значение у, то эту функцию можно рассматривать как функцию одной переменной х, и, следовательно , ставить вопрос о дифференцировании
координатной плоскости. Если зафиксировать значение у, то эту функцию можно рассматривать как функцию одной переменной х, и, следовательно , ставить вопрос о дифференцировании 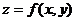 по переменой х. В этой ситуации производная
по переменой х. В этой ситуации производная  , вычисленная по переменной х, называется частной производной от f по х; она обозначается также
, вычисленная по переменной х, называется частной производной от f по х; она обозначается также  или
или 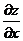 . Точно также производную функции f, вычисленную по переменной у при фиксированном х, называют частной производной функции f по у и обозначают
. Точно также производную функции f, вычисленную по переменной у при фиксированном х, называют частной производной функции f по у и обозначают 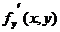 ,
, 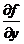 или
или 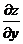 . При вычислении частных производных пользуются обычными правилами дифференцирования. В частности, если вычисляем
. При вычислении частных производных пользуются обычными правилами дифференцирования. В частности, если вычисляем  , то множитель целиком зависящий только от переменной у, можно вынести за знак производной; точно также поступаем с множителем, целиком зависящим только от переменной х при нахождении
, то множитель целиком зависящий только от переменной у, можно вынести за знак производной; точно также поступаем с множителем, целиком зависящим только от переменной х при нахождении 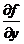 .
.
Пример. Найти частные производные функции  .
.
Решение. При вычислении  множитель
множитель 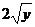 и слагаемое
и слагаемое 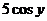 рассматриваем как постоянные величины. Следовательно,
рассматриваем как постоянные величины. Следовательно,

При вычислении 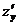 множитель
множитель 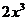 рассматриваем как постоянную величину:
рассматриваем как постоянную величину:
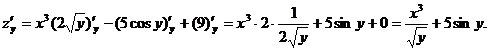
Итак, 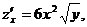
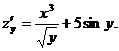
2.1.2.Частные производные высших порядков.
Частные производные 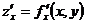 и
и 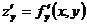 данной функции
данной функции 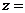
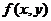 можно, в свою очередь, рассматривать как функции двух переменных х и у. Следовательно, имеет смысл ставить вопрос о нахождении уже их частных производных - производных второго порядка:
можно, в свою очередь, рассматривать как функции двух переменных х и у. Следовательно, имеет смысл ставить вопрос о нахождении уже их частных производных - производных второго порядка:
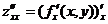 -производная дважды по х;
-производная дважды по х; 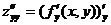 -производная дважды по у;
-производная дважды по у;
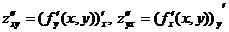 -«смешанные» частные производные второго порядка по переменным х и у.
-«смешанные» частные производные второго порядка по переменным х и у.
Для элементарных функций двух переменных результат вычисления смешанных производных на самом деле не зависит от порядка дифференцирования: 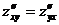 .
.
Пример. Вычислить все частные производные функции 
Решение. Cначала вычисляем производные первого порядка:

Теперь 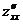
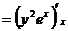
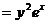 ,
, 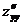
 ,
, 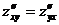
 .
.
Задачи для контрольной работы
Вычислить частные производные по переменным 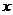 и
и 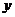 данных функций.
данных функций.
1.  . 14.
. 14. 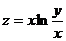 .
.
2. 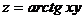 . 15.
. 15. 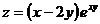 .
.
3.  . 16.
. 16. 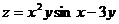 .
.
4.  . 17.
. 17. 
5. 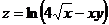 . 18.
. 18. 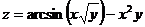 .
.
6.  . 19.
. 19.  .
.
7. 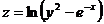 . 20.
. 20.  .
.
8.  . 21.
. 21. 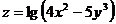 .
.
9.  . 22.
. 22. 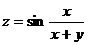 .
.
10. 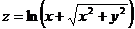 . 23.
. 23.  .
.
11. 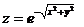 . 24.
. 24. 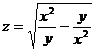 .
.
12. 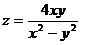 . 25.
. 25.  .
.
13. 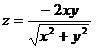 .
.
Производная неявной функции.
Неявная функция одной переменной.
Пусть зависимость переменной 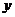 от переменной
от переменной 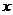 , т.е. функция
, т.е. функция 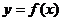 задана неявно, т.е. в виде уравнения
задана неявно, т.е. в виде уравнения 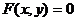 . Тогда производная функции
. Тогда производная функции 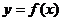 может быть вычислена в виде
может быть вычислена в виде
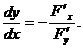
Пример. Неявная функция 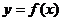 задана уравнением
задана уравнением  . Найти
. Найти 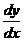 .
.
Решение. Имеем 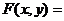
 . Теперь ищем частные производные функции
. Теперь ищем частные производные функции 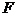 :
:
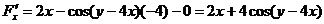 ,
,
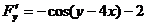 .
.
Следовательно, 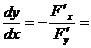
 .
.
Итак, 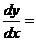
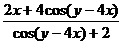 .
.
Неявная функция двух переменных.
Уравнением 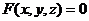 задается зависимость переменной z от переменных x и y. Если эта зависимость
задается зависимость переменной z от переменных x и y. Если эта зависимость 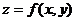 - функциональная, то имеет смысл ставить вопрос о вычислении частных производных
- функциональная, то имеет смысл ставить вопрос о вычислении частных производных  и
и 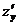 .
.
Имеют место соотношения
 ,
, 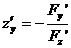 .
.
Пример. Неявная функция двух переменных задана уравнением  . Найти
. Найти  и
и 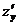 .
.
Решение. Имеем 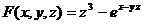 . Найдем частные производные
. Найдем частные производные 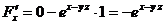 ,
, 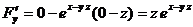 ,
, 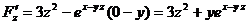 .
.
Теперь 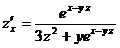 ,
,  .
.
Дата добавления: 2018-02-15; просмотров: 438; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
