Количественной характеристикой случайного события
Тема: Основные понятия теории вероятностей
4.1. Предмет изучения теории вероятностей
Течение окружающей нас действительности и нашей собственной жизни можно представить следующим образом: имеется некоторый набор условий, реализация которых (опыт) приводит всякий раз к несколько различным результатам. Например, взяли монетку в руку, подбросили и ... то ли решка, то ли орел, то ли ребром. Собрались, пошли в институт, расстояние одно и то же, но время в пути каждый раз немного разное. Земля, вращаясь по орбите вокруг Солнца, заняла определенное положение, наступила весна, которая, тем не менее, всегда неповторима.
Эти и еще множество других явлений называются случайными, т.е. от случая к случаю протекающими несколько по-иному.
Однако и в случайном есть свои закономерности.
Например, в 18 веке французский ученый Бюффон 4040 раз подряд подбросил монету, в 2048 случаях выпал герб, американский математик Пирсон в начале нашего века подбросил монету 24000 раз, из которых 12012 раз появился герб. Повторение подобного опыта приводит к тому же результату: при большом числе подбрасываний в половине случаев выпадает цифра, в половине - герб.
Время прихода в институт также колеблется вокруг некоторой средней величины.
В погоде также есть свои закономерности, которые отличают, скажем, погоду средних широт от экваториальной.
|
|
|
Теорией вероятностей называется раздел математики, изучающий закономерности массовых (т.е. повторяющихся многократно) случайных явлений .
При этом подразумевается, что набор основных условий, определяющих исход опыта, остается постоянным.
Например, на результаты артиллерийской стрельбы влияют калибр орудия, масса снаряда, заряд, угол наклона и т. д. Изменение хотя бы одного из этих условий приведет к изменению всей картины результатов попаданий.
Изучение теории вероятностей начинается с определения некоторого основного понятия, такого, как число в алгебре, вектор в векторной алгебре, матрица в линейной алгебре. Таким понятием является случайное событие.
Конкретное осуществление случайного явления, которое в результате опыта может произойти, а может и не произойти, называется случайным событием.
Например,
выпадение той или иной цифры при бросании игральной кости - случайное явление. Оно может осуществиться через следующие случайные события:
появление на верхней грани единицы, двойки, тройки, четверки, пятерки и шестерки. Обычно говорят, что опыт (бросание кости) может завершиться одним из шести исходов.
|
|
|
Случайные события обозначаются большими латинскими буквами A, B, C и т.д.
Численная мера возможности осуществления случайного события называется его вероятностью и обозначается 
и т.д.
Основная задача теории вероятностей состоит в разработке способов вычисления вероятностей различных случайных событий.
4.2. Виды случайных событий
Если появление одного из событий исключает наступление другого, они называются несовместными.
Например, выпадение одновременно и цифры и герба при бросании одной монеты.
Если же события могут произойти одновременно, то они называются совместными.
Например, при бросании двух монет могут одновременно выпасть и цифра и герб.
Если вероятности событий одинаковы, то они называются равновозможными.
Например, при бросании точно выполненной однородной игральной кости появление на верхней грани любой цифры равновозможно. Также одинакова вероятность достать любую карту из хорошо протасованной колоды.
Если в результате опыта случайное событие обязательно произойдет, оно называется достоверным.
Например, достоверное событие - замерзание чистой воды при отрицательных температурах.
|
|
|
Невозможным называется событие, которое в результате опыта никогда не наступает.
Например, появление цифры 7 при бросании игрального кубика.
Если несовместные события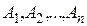 
таковы, что в результате опыта должно обязательно произойти одно из них, то говорят, что они образуют полную группу.
Например, два стрелка делают по одному выстрелу. Для этого опыта следующие события образуют полную группу:
- в мишень попали оба;
- оба промахнулись;
- первый попал, второй промахнулся;
- первый промахнулся, второй попал.
Каждое событие из полной для данного опыта группы событий часто называют исходом опыта или элементарным событием.
Если полную группу образуют два события, то они называются противоположными.
Событие, противоположное 
, обозначается 
.
Смысл события, противоположного А, состоит в ненаступлении события А.
Например, при бросании игрального кубика событие А - появление цифры 2, тогда событие, противоположное , т.е. - «не 2», а это означает, что событие - это появление цифры 1, или 3, или 4, или 5, или 6.
При бросании одной монеты событие А - выпадение цифры, а событие - выпадение герба.
4.3. Действия с событиями
|
|
|
Основными действиями с событиями являются их сумма и произведение.
Если событие состоит в осуществлении хотя бы одного из событий 
, то говорят, что событие равно сумме событий и записывают
.
Пример. Пусть А - появление четной цифры при бросании кубика, тогда 
,
где - появление двойки; 
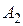- появление четверки; - появление шестерки.
Если событие состоит в совместном осуществлении событий , то говорят, что оно равно произведению событий и записывают
.
Например, если - попадание двоих стрелков в мишень при одновременной стрельбе, то 
,
где - попадание в мишень первого стрелка, 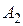- попадание второго стрелка.
Количественной характеристикой случайного события
является его вероятность.
Способ вычисления вероятности события зависит от того, исходом какого опыта является данное событие.
Рассмотрим различные варианты.
4.4. Способы непосредственного вычисления вероятностей
4.4.1. Опыт имеет конечное число равновозможных исходов
Рассмотрим опыт с бросанием двух игральных костей одновременно. Возможны следующие исходы:
Первая цифра в паре указывает цифру, выпавшую при бросании первой кости, вторая - при бросании второй.
Если событие может наступить в результате одного из 
исходов, то говорят, что они благоприятствуют . Если при этом общее число исходов опыта 
, то вероятность события равна
отношению числа исходов, благоприятствующих , к общему числу исходов: 
.
Пример. Найдем вероятность события - выпадения в сумме 5 очков при одновременном бросании двух костей.
Случаев, благоприятствующих этому событию, 4 (подчеркнуты на общей картине исходов). Значит, = 4, = 36, 
= 4/36 = 1/9.
Это определение вероятности называется классическим.
Оно позволяет получить результаты, полезные в теории вероятностей в целом. Пользуясь данным определением, можно определить рамки, в которых находится вероятность любого события.
Если взять невозможное для данного опыта событие (например, выпадение в сумме 20 очков), то = 0 и = 0.
Если же взять достоверное событие - выпадение в сумме не более 12 очков, то ему благоприятствуют все исходы, = 36, = 36/36 = 1.
Таким образом, вероятность произвольного события подчиняется следующему неравенству: 
.
4.4.2. Опыт имеет бесконечное число равновозможных исходов
Начнем с примеров. После грозы на участке между 40-м и 70-м километром произошел обрыв телефонной линии. Какова вероятность события , состоящего в том, что обрыв произошел между 50-м 55-м километром?
Будем считать, что обрыв может произойти в любой точке линии с одинаковой возможностью. Тогда все возможные исходы опыта находятся на отрезке длиной 30 км, а исходы, которые нас интересуют, на отрезке длиной 5 км.
В качестве вероятности естественно взять отношение длин отрезков:
.
Например, загадываются два числа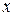 
и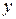 
от нуля до единицы. Тут возможно бесконечное число вариантов, которые находятся внутри квадрата с единичной стороной, показанного на рисунке.
Если нас интересуют такие числа, сумма которых не больше 1, т.е. 
, то они лежат внутри заштрихованного треугольника.
Так как площадь этого треугольника составляет половину от площади, представляющей все исходы опыта, то вероятность, что пара чисел 
будет удовлетворять требованию , равна 1/2.
В других случаях, например, при загадывании тройки чисел, все исходы некоторого опыта и исходы, благоприятствующие определенному событию, могут быть представлены объемом некоторого тела и его частью.
Поэтому можно дать такое общее определение. Если все возможные исходы опыта можно представить областью 
(длиной отрезка, площадью фигуры, объемом тела), а благоприятствующие событию исходы - частью этой области 
, то вероятность события можно найти по формуле:
Это геометрическое определение вероятности, полезное и при решении ряда задач и для иллюстраций.
4.4.3. Опыт, вероятность различных исходов которого нельзя предсказать заранее
Например, на первый взгляд, рождение мальчика или девочки одинаково возможно. Однако многочисленные статистические данные, которые иллюстрирует небольшая таблица, опровергают это предположение.
| Страна | Год | Всего родилось детей | Из них мальчиков | Доля мальчиков |
| Польша | 1927 | 958733 | 496544 | 0,518 |
| Швеция | 1935 | 88682 | 45682 | 0,517 |
Такие сведения характерны для разных стран и периодов времени.
В таких случаях вероятность события определяется следующим образом. Если - число появлений события в опытах, то отношение 
называется частотой события .
За вероятность события принимается постоянная величина, равная средней частоте события при большом числе опытов.
Это определение вероятности называется статистическим.
Пример. При проверке работы цеха в первый раз из 100 деталей было обнаружено 2 бракованных, во второй раз – 3, в третий – 1 деталь, значит,
Тогда за вероятность обнаружить бракованную среди деталей этого цеха можно принять среднюю частоту:
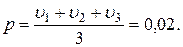
Дата добавления: 2021-06-02; просмотров: 69; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!