Задача об определении оптимального ассортимента продукции
Симплексный метод решения линейных задач.
Наиболее эффективным методом решения задач линейного программирования является алгоритм, известный под названием симплексный метод, или метод последовательного улучшения плана. Симплексный метод – это итерационный процесс, который начинается с одного решения и в поисках лучшего варианта движется по области возможных значений до тех пор, пока не достигнет оптимального значения (в частности движение выполняется по угловым точкам многоугольника решений, полученного графическим (геометрическим) методом).
В основе симплексного метода решения задач линейного программирования лежит метод последовательных исключений, представляющий собой совокупность удобных вычислительных алгоритмов, построенных на последовательном применении тождественных (симплексных) преобразований системы уравнений. При выполнении симплексных преобразований для упрощения вычислений можно использовать так называемые симплексные таблицы – полные или укороченные, имеющие определенный шаблон. Каждое симплексное преобразование системы сводится к переходу от одной симплексной таблицы к другой, от одного допустимого решения системы уравнений к другому – улучшенному. Так достигается оптимальное решение.
Прежде всего, остановимся на форме записи задачи для решения ее симплексным методом.
Задача линейного программирования (ЗЛП) может формулироваться:
|
|
|
1) в общей форме;
2) в стандартной форме;
3) в канонической форме.
ЗЛП в общей форме может иметь:
a) неотрицательные и отрицательные среди ограничивающих выражений неизвестные переменные;
b) среди ограничивающих выражений могут быть строгие равенства (=) и неравенства разного вида ( <, >);
c) вид экстремума целевой функции может быть любой (max или min).
ЗЛП в стандартной форме может иметь:
a) все неизвестные переменные неотрицательны;
b) все ограничивающие выражения являются неравенствами вида ( < );
c) любой вид экстремума функции (max, min).
ЗЛП в канонической форме должна иметь:
a) все переменные неотрицательны xi > 0;
b) все ограничивающие условия в виде строгих равенств;
c) максимизируемую целевую функцию.
При решении задачи симплексным методом необходимо преобразовать форму записи исходных данных в каноническую форму.
Правила приведения ЗЛП к канонической форме:
1. Для преобразования неравенства вида (<) в ограничение в виде равенства (=), нужно ввести новую неотрицательную переменную, прибавить ее в левую часть исходного неравенства и заменить в нем символ «<» на «=».
2. Для преобразования неравенства вида (>) в строгое равенство необходимо умножить обе части неравенства на (-1), при этом знак неравенства изменится на противоположный. Затем по правилу «один» ввести новую неотрицательную переменную в левую часть неравенства, и заменить в нем символ неравенства на строгое равенство.
|
|
|
3. Чтобы из целевой функции Z(x)→ min получить Z(x)→ max необходимо у первой поменять знаки всех коэффициентов на противоположный и изменить вид экстремума.
Далее в соответствии с исходной системой уравнений составляется первая симплексная таблица, затем выполняется алгоритм симплексного преобразования.
Алгоритм симплексного преобразования:
1. Выбирается разрешающий (или ключевой) столбец – k, соответствующий наименьшему отрицательному элементу в Z-строке (так называют строку таблицы, которая соответствует целевой функции Z) при Z(x)→ max.
2. Выбирается разрешающая (или ключевая) строка – r, которая соответствует наименьшему положительному из отношений элементов bi правой части уравнений к соответствующим элементам aik разрешающего столбца:
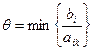 .
.
3. На пересечении разрешающих столбца и строки стоит разрешающий (генеральный) элемент (РЭ)– a rk.
|
|
|
4. Выполняются правила заполнения новой симплекс-таблицы.
В случае решения задачи методом укороченных симплексных таблиц правила заполнения новой симплекс-таблицы следующие:
1) меняем местами БП и СП: переменная ключевой строки (базисная переменная) выводится из базиса; в новой симплекс-таблице на ее место в базис вводится переменная из ключевого столбца (свободная переменная);
2) на месте РЭ стоит величина ему обратная;
3) новые значения ключевой строки получают, разделив старые элементы на разрешающее число:  ;
;
4) новые значения элементов ключевого столбца получают, разделив старые элементы на разрешающее число, и поменяв знак на противоположный;
5) все остальные новые элементы таблицы определяются по формуле (на основе «правила прямоугольника»):
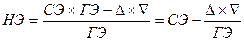 ;
;
 |
схема расположения элементов формулы в таблице:
∆ – элемент находится в разрешающей строке, в одном столбце со старым элементом;
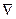 – элемент находится в разрешающем столбце, в одной строке со старым элементом;
– элемент находится в разрешающем столбце, в одной строке со старым элементом;
5. В новой таблице содержится новое допустимое решение. Если в новой симплекс-таблице, в Z-строке, найдется хотя бы один отрицательный элемент (при решении задачи на максимум целевой функции), то решение можно улучшить. Необходимо повторить алгоритм симплексных преобразований. Если все элементы в Z-строке неотрицательны, то достигнуто оптимальное решение.
|
|
|
Рассмотрим симплексный метод на основе укороченных таблиц на исходных данных задачи об определении оптимального ассортимента продукции.
Задача об определении оптимального ассортимента продукции
Задача. Предприятие может производить два вида изделий А и В, располагая для их изготовления ограниченными ресурсами материала чугуна и стали соответственно в количестве 350 и 392 кг и оборудования в количестве 408 станко-часов. Данные, представленные в таблице, характеризуют затраты каждого из перечисленных трех видов ресурсов на изготовление одного вида изделия А и В.
Требуется определить сколько изделий А и В должно производить предприятие, чтобы достичь наибольшей прибыли.
Таблица 1.
| Виды ресурсов | Объем ресурсов (кг) | Затраты на одно изделие (кг) | |
| А | В | ||
| Чугун | 350 | 14 | 5 |
| Сталь | 392 | 14 | 8 |
| Оборудование | 408 | 6 | 12 |
| Прибыль в руб. | 10 | 5 | |
Введем искомые неизвестные: x1 – число изделий А; x2 – число изделий В; – которые должно производить предприятие:  .
.
Математическую модель задачи можно сформулировать следующим образом: среди множества неотрицательных решений системы неравенств:
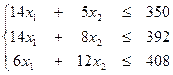 (1)
(1)
найти такое решение, для которого функция Z = 10x1 + 5x2 – достигает наибольшего значения.
Добавляя к левой части неравенств в системе (1) некоторую неотрицательную величину:
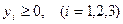 , (2)
, (2)
называемую выравнивающей, или базисной переменной, превратим их в уравнения (3):
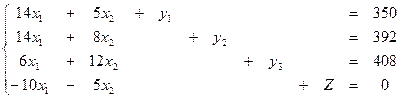 (3)
(3)
Каждая из переменных y1, y2, y3 входит только в одно уравнение и зависит от переменных x1 и x2, которые называются свободными.
Систему уравнений (3) задачи представим в виде:
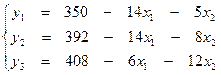 (4)
(4)
Целевую функцию перепишем в виде:
 (5)
(5)
Составляем первую укороченную симплекс-таблицу в соответствии с системой уравнений (4):
Таблица 1.
| Базисные переменные (БП)
| Свободные переменные (СП) | 1 | |
| (-x1) | (-x2) | ||
| y1 | 14 | 5 | 350 |
| y2 | 14 | 8 | 392 |
| y3 | 6 | 12 | 408 |
| Z | -10 | -5 | 0 |
В таблице 1 содержится первое (исходное) допустимое базисное решение системы уравнений (4):
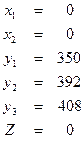 ;
;
Так как в симплекс-таблице, в Z-строке, стоят отрицательные элементы, то решение можно улучшить.
Выполняется алгоритм симплексного преобразования и заполнение новой симплекс-таблицы (таблица 2).
В соответствии с алгоритмом:
1. Выбираем ключевой столбец – по значению -10 в Z-строке.
2. Выбираем ключевую строку:
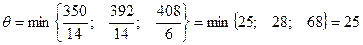 ;
;
Наименьшему из отношений соответствует 1 строка – это ключевая строка.
3. Генеральный элемент: ark=14.
4. Заполняем новую симплекс-таблицу – таблицу 2, в соответствии с правилами; из базиса выводится переменная y1, и вводится переменная x1.
Таблица 2.
| Базисные переменные (БП)
| Свободные переменные (СП) | 1 | |
| (-y1) | (-x2) | ||
| x1 | 1/14 | 5/14 | 25 |
| y2 | -(14/14) | 3 | 42 |
| y3 | -(6/14) | 138/14 | 258 |
| Z | +(10/14) | -(20/14) | 250 |
В таблице 2 содержится второе допустимое решение системы уравнений (4):

Так как в Z-строке имеется отрицательный элемент, то решение можно улучшить. Необходимо повторить алгоритм симплексных преобразований и составить новую симплекс-таблицу – таблицу 3.
Выполняем преобразования в соответствии с алгоритмом:
1. Выбираем ключевой столбец – по отрицательному значению -20/14 в Z-строке.
2. Выбираем ключевую строку:
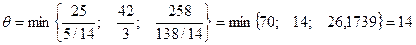 ;
;
Наименьшему из отношений соответствует 2 строка – это ключевая строка.
3. Генеральный элемент: ark=3.
4. Заполняем новую симплекс-таблицу – таблицу 3, в соответствии с правилами, из базиса выводится переменная y2, и вводится переменная x2.
Таблица 3.
| Базисные переменные (БП)
| Свободные переменные (СП) | 1 | |
| (-y1) | (-y2) | ||
| x1 | 4/21 | -(5/42) | 20 |
| x2 | -(1/3) | 1/3 | 14 |
| y3 | 20/7 | -(23/7) | 120 |
| Z | 5/21 | 10/21 | 270 |
В таблице 3 содержится третье допустимое решение системы уравнений (4):

Так как в Z-строке нет отрицательных элементов, то решение является оптимальным.
Таким образом, максимальная прибыль в 270 руб. будет получена, если предприятие произведет 20 изделий вида А и 14 изделий вида В.
Z=10 × 20 + 5 × 14 = 270 руб.
С геометрической точки зрения, тождественные преобразования по симплексному методу представляют собой последовательные движения от одной вершины выпуклого многоугольника решений к соседней, от нее – к следующей, и так, по сторонам этого многоугольника – к оптимальной вершине.
Экономическая сущность метода заключается в том, что этот метод дает возможность, выбрав отправной – опорный план действий, постепенно передвигаться вперед, и в конечном итоге достичь оптимального плана.
Дата добавления: 2021-06-02; просмотров: 476; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
