Логарифм произведения, сумма логарифмов
Логарифм произведения равен сумме логарифмов сомножителей.

Пример. Представить 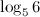 в виде суммы логарифмов.
в виде суммы логарифмов.
Решение. 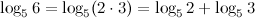
Верно и обратное: сумма логарифмов равна логарифму произведения подлогарифмических выражений.

Пример. Упростить 
Решение. 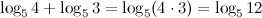
Логарифм частного, разность логарифмов
Логарифм частного (дроби) равен разности логарифмов сомножителей.

Пример. Известно, что  , а
, а  . Выразить
. Выразить  через
через  и
и  .
.
Решение. 
Верно и обратное утверждение: разность логарифмов равна логарифму частного подлогарифмических выражений.

Пример. Вычислить значение выражения 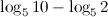
Решение. 
Логарифм степени
Логарифм степени равен произведению показателя степени на логарифм ее основания.

Пример. Вычислить 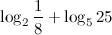
Решение. 

Верно и обратное: коэффициент перед логарифмом можно вносить в степень подлогарифмической функции.

Пример. Упростить выражение 
Решение. 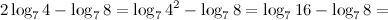

Логарифм корня
Логарифм корня равен частному от деления логарифма подкоренного выражения на показатель корня.

Пример. Вычислить  , если
, если 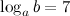
Решение. 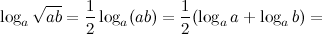
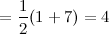
Верно и обратное: можно вносить числа, стоящие перед знаком логарифма, в сам логарифм.

Пример. Упростить выражение 
Решение. 

Число е

Определение
Число е - математическая константа, являющаяся трансцендентным числом. Чаще всего называется числом Эйлера, реже - числом Непера.
|
|
|
Трансцендентное число - это число, которое не может быть корнем полинома с целыми коэффициентами.
Примечание
Способ помнить число е простой - два, семь, дважды Лев Толстой.
P.S. Лев Николаевич Толстой родился в 1828 году.
Натуральный логарифм
Для различного рода теоретических и практических исследований наиболее удобным основанием логарифма является иррациональное число  .
.
Определение
Натуральным логарифмом называется логарифм по основанию  . Такие логарифмы обозначаются символом ln. Запись
. Такие логарифмы обозначаются символом ln. Запись  означает тоже самое, что и
означает тоже самое, что и 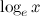 .
.
Основание натурального логарифма - число е.
Десятичный логарифм
Десятичный логарифм - логарифм по основанию 10. Обозначается знаком lg, т.е.  . Основание десятичного логарифма - число 10.
. Основание десятичного логарифма - число 10.
Тогда из определения логарифма можно заключить, что десятичный логарифм  - это решение показательного уравнения
- это решение показательного уравнения  .
.
Логарифмическая функция
Функция, которую можно записать формулой  , называется логарифмической функцией.
, называется логарифмической функцией.
Логарифмическая функция является обратной функцией к показательной 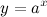 . Поэтому графики этих функций симметричны относительно биссектрисы первой и третьей координатных четвертей.
. Поэтому графики этих функций симметричны относительно биссектрисы первой и третьей координатных четвертей.
|
|
|
Свойства логарифмической функции
1° Область определения - 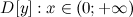
2° Область значений - 
3° Четность/нечетность - функция общего вида (функция ни четная, ни нечетная)
4° Нули функции - 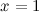
5° Интервалы монотонности, экстремум функции - график функции возрастает
на  при
при  ; убывает на
; убывает на  при
при  ; точек экстремума нет.
; точек экстремума нет.
6° Интервалы выпуклости/вогнутости - Функция выпукла на
промежутке  при
при  ; функция вогнута на промежутке
; функция вогнута на промежутке  при
при  точек перегиба нет.
точек перегиба нет.
7° График логарифмической функции:

Логарифмические уравнения
Логарифмическое уравнение - это такое уравнение, в котором неизвестная стоит под знаком логарифма.
При решении логарифмических уравнений часто приходится логарифмировать или потенцировать обе части уравнения, что не всегда может привести к равносильным уравнениям.
Логарифмировать алгебраическое выражение - значит выразить его логарифм через логарифмы отдельных чисел, входящих в это выражение.
Пример
Задание. Прологарифмировать выражение 
Решение. В левой и правой части допишем логарифм по основанию  :
:
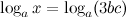
По свойствам логарифмов логарифм произведения, стоящий в правой части, представим как сумму логарифмов от каждого из сомножителей, то есть:
|
|
|

Определение
Если по данному результату логарифмирования находят выражение, от которого получен этот результат, то такая операция называется потенцированием.
Пример
Задание. Пропотенцировать выражение 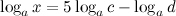
Решение. Используя свойства логарифмов, преобразуем правую часть данного выражения:

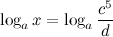

1. Простейшим логарифмическим уравнением является уравнение  , причем основание логарифма
, причем основание логарифма 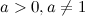 , а подлогарифмическое выражение
, а подлогарифмическое выражение  .
.
Для любого действительного  это уравнение имеет единственное решение
это уравнение имеет единственное решение  .
.
Пример
Задание. Решить уравнение 
Решение. Вначале находим область допустимых значений (ОДЗ):  , тогда единственное решение уравнения
, тогда единственное решение уравнения 
Ответ. 
2. Логарифмическое уравнение вида 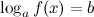
Здесь 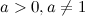 ,
, 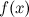 - элементарная алгебраическая функция, причем, чтобы уравнение имело решение, должно выполняться неравенство
- элементарная алгебраическая функция, причем, чтобы уравнение имело решение, должно выполняться неравенство 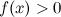 .
.
Заменой 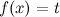 данное уравнение приводится к простейшему логарифмическому уравнению
данное уравнение приводится к простейшему логарифмическому уравнению 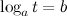 , решение которого приведено в пункте 1.
, решение которого приведено в пункте 1.
Пример
Задание. Решить уравнение 
Решение. ОДЗ: 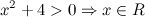
Замена:  , получаем уравнение
, получаем уравнение  , решение которого
, решение которого

Делая обратную замену, получаем:

Ответ. 
Пример
Задание. Найти решение уравнения  .
.
Решение. ОДЗ: 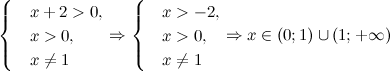
|
|
|
Замена: 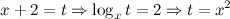 . Делая обратную замену, приходим к уравнению
. Делая обратную замену, приходим к уравнению

Второй корень не принадлежит ОДЗ, а значит решение 
Ответ. 
3. Логарифмическое уравнение вида 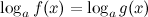
Здесь  - отличное от единицы положительное число;
- отличное от единицы положительное число; 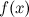 и
и  - элементарные алгебраические функции.
- элементарные алгебраические функции.
Решение логарифмических уравнений такого типа сводится к решению уравнения  . Поэтому для решения рассматриваемого типа уравнений
. Поэтому для решения рассматриваемого типа уравнений 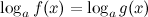 достаточно найти все решения уравнения
достаточно найти все решения уравнения  и среди полученных выбрать те, которые относятся к ОДЗ уравнения
и среди полученных выбрать те, которые относятся к ОДЗ уравнения 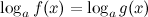 . Если уравнение
. Если уравнение  решений не имеет, то их не имеет и исходное логарифмическое уравнение.
решений не имеет, то их не имеет и исходное логарифмическое уравнение.
Пример
Задание. Решить уравнение 
Решение. Находим ОДЗ: 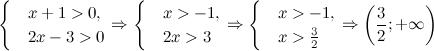
Решаем уравнение  :
: 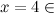 ОДЗ.
ОДЗ.
Итак, решением исходного логарифмического уравнения также является это значение.
Ответ.  .
.
Логарифмические неравенства
Логарифмическим неравенством называется неравенство, в котором неизвестная величина стоит под знаком логарифма.
1. Неравенство  в случае, если
в случае, если  сводится к равносильному неравенству
сводится к равносильному неравенству 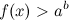 . Если же
. Если же  - то к неравенству
- то к неравенству  .
.
Аналогично неравенство  равносильно неравенствам для
равносильно неравенствам для  :
:  ; для
; для  :
: 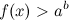 .
.
Решения полученных неравенств надо пересечь с ОДЗ: 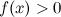
Пример
Задание. Решить неравенство 
Решение. ОДЗ: 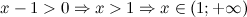
Учитывая выше написанное, получаем, что заданное логарифмическое неравенство равносильно неравенству:
 или
или 
В пересечении с ОДЗ получаем, что 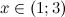
Ответ. 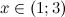 .
.
2. Решение логарифмического неравенства вида  равносильно решению следующих систем:
равносильно решению следующих систем:
а) 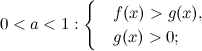 б)
б) 
Неравенство 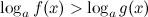 в каждом из двух случаев сводится к одной из систем:
в каждом из двух случаев сводится к одной из систем:
а)  б)
б) 
Пример
Задание. Решить неравенство 
Решение. Данное неравенство равносильно системе:

Ответ. 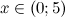
Дата добавления: 2021-06-02; просмотров: 125; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
