Задание № 4. Численное интегрирование.
Вычислить интеграл 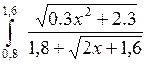 методом Симпсона и методом левых прямоугольников с шагом интегрирования h =
методом Симпсона и методом левых прямоугольников с шагом интегрирования h = 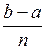 , где n = 50.
, где n = 50.
Задание № 5. Численное решение задачи Коши для обыкновенных дифференциальных уравнений.
Решить дифференциальное уравнение 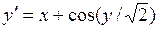 при начальных условиях
при начальных условиях 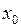 = 0.8, y(
= 0.8, y( 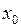 ) = 1.4 с шагом интегрирования h = 0.1 на интервале [0.8;1.8] методом Рунге-Кутта.
) = 1.4 с шагом интегрирования h = 0.1 на интервале [0.8;1.8] методом Рунге-Кутта.
Задание № 6. Численное решение систем обыкновенных дифференциальных уравнений.
Решить систему обыкновенных дифференциальных уравнений методом Эйлера с шагом интегрирования h = 0.1
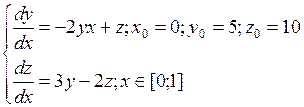
ВАРИАНТ 9
Задание № 1. Численное решение уравнений.
Найти корень уравнения 2 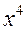 - 8
- 8 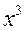 + 8
+ 8 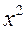 - 1 = 0 методом половинного деления и методом касательных с точностью
- 1 = 0 методом половинного деления и методом касательных с точностью  .
.
Задание № 2. Численное решение систем линейных алгебраических уравнений.
Решить систему линейных алгебраических уравнений методом простых итераций с точностью  .
.

Задание № 3. Численное решение систем нелинейных уравнений.
Решить систему нелинейных уравнений методом простых итераций с точностью  . Начальное приближение принять
. Начальное приближение принять 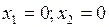 .
.
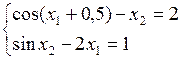
Задание № 4. Численное интегрирование.
Вычислить интеграл  методом Симпсона и методом трапеций с шагом интегрирования h =
методом Симпсона и методом трапеций с шагом интегрирования h = 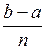 , где n = 50.
, где n = 50.
Задание № 5. Численное решение задачи Коши для обыкновенных дифференциальных уравнений.
Решить дифференциальное уравнение 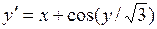 при начальных условиях
при начальных условиях 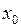 = 1.2, y(
= 1.2, y( 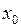 ) = 2.1 с шагом интегрирования h = 0.1 на интервале [1.2, 2.2] методом Рунге-Кутта.
) = 2.1 с шагом интегрирования h = 0.1 на интервале [1.2, 2.2] методом Рунге-Кутта.
Задание № 6. Численное решение систем обыкновенных дифференциальных уравнений.
Решить систему обыкновенных дифференциальных уравнений методом Эйлера с шагом интегрирования h = 0.1
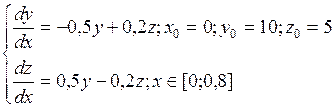
ВАРИАНТ 10
Задание № 1. Численное решение уравнений.
Найти корень уравнения 3 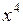 + 8
+ 8 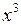 x +
x + 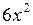 - 10 = 0 методом половинного деления и методом хорд с точностью
- 10 = 0 методом половинного деления и методом хорд с точностью  .
.
Задание № 2. Численное решение систем линейных алгебраических уравнений.
Решить систему линейных алгебраических уравнений методом простых итераций с точностью  .
.
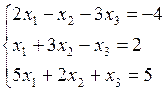
Задание № 3. Численное решение систем нелинейных уравнений.
Решить систему нелинейных уравнений методом простых итераций с точностью  . Начальное приближение принять
. Начальное приближение принять 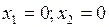 .
.
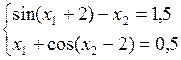
Задание № 4. Численное интегрирование.
Вычислить интеграл 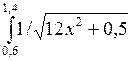 методом Симпсона и методом трапеций с шагом интегрирования h =
методом Симпсона и методом трапеций с шагом интегрирования h = 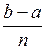 , где n = 50.
, где n = 50.
Задание № 5. Численное решение задачи Коши для обыкновенных дифференциальных уравнений.
Решить дифференциальное уравнение 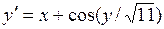 при начальных условиях
при начальных условиях 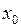 = 2.1, y(
= 2.1, y( 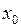 ) =2.5 с шагом интегрирования h = 0.1 на интервале [2.1,3.1] методом Эйлера.
) =2.5 с шагом интегрирования h = 0.1 на интервале [2.1,3.1] методом Эйлера.
Задание № 6. Численное решение систем обыкновенных дифференциальных уравнений.
Решить систему обыкновенных дифференциальных уравнений методом Эйлера с шагом интегрирования h = 0.1
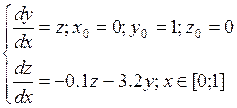
Дата добавления: 2021-06-02; просмотров: 59; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
