При выполнении заданий 13-18 запишите ход решения и полученный ответ
Консультация по учебной дисциплине «МАТЕМАТИКА»
Перечень требований по всем разделам включает в себя требования к уровню подготовки обучающихся по математике, освоивших программу среднего (полного) общего образования (базовый уровень).
Требования (умения и виды деятельности), проверяемые заданиями письменной экзаменационной работы
Уметь выполнять вычисления и преобразования:
-выполнять арифметические действия, сочетая устные и письменные приемы;
-находить значения корня натуральной степени, степени с рациональным показателем, логарифма;
-вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
-проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Уметь решать уравнения и неравенства:
-решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы;
-решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
-использовать для приближенного решения уравнений и неравенств графический метод;
-решать рациональные, показательные и логарифмические неравенства.
Уметь выполнять действия с функциями:
-определять значение функции по значению аргумента при различных способах задания функции;
|
|
|
-вычислять производные и первообразные элементарных функций;
-исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций.
Уметь выполнять действия с геометрическими фигурами, координатами и векторами:
-решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);
-решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
-использовать при решении стереометрических задач планиметрические факты и методы;
-определять координаты точки.
Уметь строить и исследовать простейшие математические модели:
-моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи;
-исследовать построенные модели с использованием аппарата алгебры;
-моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры;
-решать практические задачи, связанные с нахождением геометрических величин;
-проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений.
|
|
|
1.(1 балл) Билет на автобус стоит 20 руб. Определите на сколько поездок хватит 300 руб, если стоимость билета снизят на 10 %.
Решение:
(20*10):100=2(руб)- скидка
20-2=18 (руб)- стоимость билета со скидкой.
300:18=16,66 или на 16 поездок хватит 300 руб.
Ответ: 16
2. (1 балл) Участок для строительства новой школы имеет форму прямоугольника, стороны которого равны 650 м. и 300 м. Данный участок необходимо обнести забором. Найдите длину этого забора, если в нем планируется сделать ворота, длиной 5 метров. Ответ дайте в метрах.
Решение:
Р=2(650+300) =1900(м)
1900-5=1895(м)- длина забора
Ответ: 1895
3. (1 балл) Установите соответствие между величинами и их возможными значениями:
ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ
А) Скорость движения велосипедиста
Б) Скорость полета космического корабля
В) Скорость распространения света
Г) Скорость движения улитки
1) 0,4 м/мин
2) 15 км/ч
3) 20 000 км/ч
4) 300 000 км/с
Решение:
А-2, Б-3, В-4, Г-1
Ответ: 2341
4. (1 балл) Вычислите значение выражения 
Решение:  =25
=25
Ответ: 25
5. (1 балл) Найдите значение cos  , если известно, что sin
, если известно, что sin  =
=  и
и  1 четверти.
1 четверти.
Решение:
cos  =
=  =
=  =
=  =
= 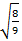 =
= 
Ответ: 
6. (1 балл) Решите уравнение 35х+1= 92х
Решение:
35х+1= 92х
35х+1= 34х
5х+1=4х
х=-1
Ответ: -1
7. (1 балл) Найдите промежутки возрастания функции f(x)=2x4-2x3-x2+2
|
|
|
Решение:
f(x)=2x4-2x3-x2+2
f  (x)=8x3-6x2- 2x
(x)=8x3-6x2- 2x
8x3-6x2- 2x=0
8x3-6x2- 2x
2х(8x3-6x2- 2x)=0
х1=0,
8x3-6x2- 2x=0, Д=25, х2=1, х3=- 
Ответ: (-  ;0)
;0) 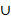 (1;
(1; 
8. (1 балл) Решите уравнение 4х 2х²+1=16
Решение: 4х 2х²+1=16
22х 2х²+1=16
22х+х²+1=24
х2+2х-3=0
х1=-3, х2=1
Ответ: -3; 1
9. (1 балл) Определите, какой из ниже приведенных графиков соответствует четной функции. Отметьте его знак «+» и кратно поясните, почему
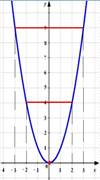

Рис 1. Рис.2
Используя график функции у= f ( x ) , определите и запишите ответ:
10.(1балл) наименьшее и наибольшее значения функции;
11.(1балл) промежутки возрастания и убывания функции;
12.(1 балл) при каких значениях х f(x) 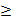 0
0
Решение:
9. Рис.1-четная функция;
10. Уmin=0, при х=0;
11.На промежутке (- 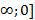 - функция убывает, а на промежутке [0;+
- функция убывает, а на промежутке [0;+ 
12.Функция принимает положительные значения на множестве (- 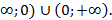
При выполнении заданий 13-18 запишите ход решения и полученный ответ
13. (1 балл) Найдите первообразную функции f(x)= 8x3+3x2-2, график которой проходит через точку А(-1;2)
Решение:
f(x)= 8x3+3x2-2
F(x)=2x4+x3-2x+C
2=2-1+2+C
C=-1
F(x)=2x4+x3-2x-1
Ответ: F(x)=2x4+x3-2x-1
14. (1 балл) В сборнике билетов по математике всего 88 билетов, в 11 из них встречается вопрос по стереометрии. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по стереометрии.
|
|
|
Решение: m=11, n=88, P(x)=  =
=  . Ответ:
. Ответ: 
15. (1 балл)

Ответ: АС=4  , СD=4
, СD=4
16. (1 балл) Решите уравнение lg2x-7lgx=8
Решение:
lg2x-7lgx=8
lg2x-7lgx-8=0
lgx=a
a2-7a-8=0
a1=8, a2=-1
1) lgx=8 2) lgx=-1
x=108 x=10-1
Ответ: 108, 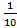
17. (1 балл) Решите тригонометрическое уравнение cos2x+cos2x= 
Решение: cos2x+cos2x= 
cos2x+  cos2x=
cos2x=  -
- 
 cos2x=
cos2x= 
cos2x= 
2х=  + 2
+ 2  +
+ 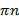 ,
,  Z Ответ:
Z Ответ:  +
+ 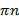 ,
,  Z
Z
20. Основанием прямой призмы является ромб со стороной 12 см и углом 600. Меньшее из диагональных сечений призмы является квадратом. Найти объем призмы.
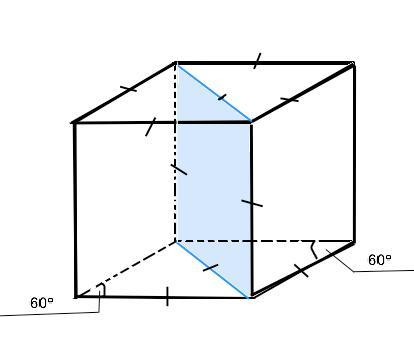
Решение:
Так как основание призмы ромб с острым углом 60°, меньшая диагональ делит его на два равносторонних треугольника с равными углами при их основании (меньшей диагонали). Поэтому высота призмы равна этой диагонали как сторона квадратного сечения, т.е. h=12 см. Объём призмы находят произведением площади основания на высоту ромба.
V=S•h.
Площадь параллелограмма равна произведению соседних сторон на синус угла между ними. Ромб - параллелограмм с равными сторонами. S=a²•sin60°=12²•√3/2=72√3 см² ⇒
V=72√3•12=864√3 см³
Ответ: 864√3 см³
Дата добавления: 2021-05-18; просмотров: 55; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
