Список источников информации и иллюстраций
Международный Фестиваль «Звезды Нового Века» - 2020
Точные науки (от 8 до 17 лет)
«ЕСЛИ ИЗМЕНИТЬ УСЛОВИЕ ИЛИ ЗАДАНИЕ
В ЗАДАЧАХ ПО ПЛОСКИМ КРИВЫМ»
Шахабутдинова Регина 15 лет,
ученица 9-го класса
Руководитель работы:
Дыхова Лариса Владимировна,
учитель математики
МОУ СОШ № 14
г. Киселёвск Кемеровской области
2020 г.
Содержание
Введение……………………………………………………………………………….. 3
1 Овоид яйцевидный……….…………………………………………………………. 5
2 Завитки………………………………………………………………………………. 6
3 Парабола. Цепная линия……………………………………………………………. 7
4 Циклические кривые………………………………………………………………... 10
4.1 Циклоида…………………………………………………………………………….. 13
4.2 Гипоциклоида……………………………………………………………………….. 18
4.3 Эпициклоида……………………………………………………………………….. 22
5 Линия изогнутой гибкой рейки…………………………………………………….. 25
Заключение……………………………………………………………………………… 26
Список источников информации и иллюстраций…………………………………… 27
Введение
Кривые линии повсеместно встречаются в окружающем нас мире. Это траектории движущихся объектов, очертания инженерных конструкций и деталей машин, границы и результат пересечения поверхностей и т.п. Кривые, все точки которых принадлежат одной плоскости, называются плоскими, остальные – пространственными. В данной работе исследованы плоские кривые. [2, с.94]
|
|
|
Возникла проблема: если решать задачи по плоским кривым, как изменится их вид при изменении условия или задания.
И обозначилась цель исследовательской работы: выявление результата при изменении условия или задания в задачах по плоским кривым.
Для достижения поставленной цели необходимо решить следующие задачи:
- определить, с какими плоскими кривыми провести исследование;
- выявить, придумать и решить задачи по плоским кривым с изменением условия или задания.
Гипотеза: Если изменить условие или задание в задачах по плоским кривым, то получаются различные интересные варианты их исполнения.
Объект исследования: кривые линии.
Предмет исследования: плоские кривые линии (циркульные и лекальные).
Методы исследования: теоретические и практические: изучение плоских кривых и решение задач с их применением.
Самой объёмной и очень интересной в работе стала тема циклических кривых. Для исследования взяты циклоида, гипоциклоида и эпициклоида.
|
|
|
Дуга, описываемая точкой А между двумя соседними начальными точками, называется аркой циклоиды.
Рисунок 1
В ходе исследования было обращено внимание на названия большинства циклических кривых. Возник вопрос при названии гипоциклоид с семью арками. Они выглядят вот так (рис.2 и 3):
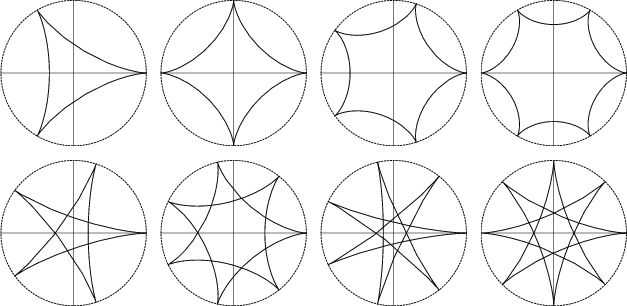Рисунок 2 Рисунок 3 
Рисунок 4 
Рисунок 5
И называются одинаково: гипоциклоида с семью арками. Но как их различать? В своей предыдущей исследовательской работе «Велика ли роль числовых приставок» был выявлен счёт от 1 до 10 греческих приставок: 1 –моно, 2 – би, 3 – три, 4 –тетра, 5 – пента, 6 – гекса, 7 – гепта, 8 – окто; 9 –нона и 10 – дека. А ещё в одной работе «Что умеет школьный циркуль?» были выявлены звёздчатые многоугольники, например, гептаграмма 7/2: в названии приставка гепта означает греческое число 7, а 7/2 означает, что окружность разделили на 7 равных частей и соединили каждую вторую точку на окружности (рисунок 4); 7/3 – соединили каждую третью точку (рис.5).
Теперь придумываем названия большинства циклических кривых на греческий лад.
Арка – по-гречески Αψίδα (апсида). Читается очень просто по буквам:
Α – альфа, ψ – пси, ί –йота, δ – дельта, α - альфа.
|
|
|
Например, рисунок 2 – это: гипоциклоида с семью арками по-гречески может называться так: гипосептаапсида 7/2; рисунок 3 - гипосептаапсида 7/3.
На основе вышеизложенного в качестве эксперимента были даны греческие названия всем приведённым циклическим кривым.
Овоид яйцевидный
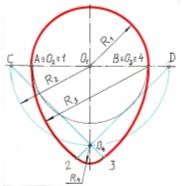
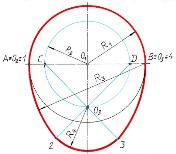
Овоид – замкнутая циркульная коробовая кривая, имеющая одну ось симметрии. [7,с.28]
| Задача | Решение | Пояснение | |||
| 1.1 | Построить яйцевидный овоид нормальной формы | 
| Из центра О1 провести окружность радиусом R1=АВ/2 и на вертикальной оси отметить точку О4. Провести прямую АВ. Из центров А и В провести дуги окружностей радиусом R2 =АВ до пересечения с прямыми АО4 и ВО4 в точках 2 и 3. Замыкающую дугу радиусом R3 = О42 провести из центра О4. | ||
| 1.2 | Изменить задание задачи 1.1 |
|
Провести вспомогательную окружность радиусом R2 > R1.
| ||
| Построить яйцевидный овоид острой формы | |||||
| 1.3 | Изменить задание задачи 1.1 |
|
Провести вспомогательную окружность радиусом R2 < R1.
| ||
| Построить яйцевидный овоид тупой формы | |||||
| Вывод: Приизменении задания меняем радиус вспомогательной полуокружности, в результате чего и получаются овоиды разной формы. Если яйцевидный овоид вращать вокруг вертикальной оси, получится тело вращения, похожее на куриное яйцо. Действительно, куриные яйца бывают нормальной, острой и тупой формы.
| |||||
Завитки
Завиток представляет собой плоскую незамкнутую циркульную составную кривую, по форме похожую на спираль и состоящую из нескольких дуг различный радиусов, проведённых из нескольких центров. При построении радиус каждой последующей дуги увеличивается на радиус первой дуги. [5, с.34; 6, с.108]
| Задача | Решение | |
| 2.1 | Построить завиток из двух центров, или завиток, «глазками» которого является окружность радиуса R. |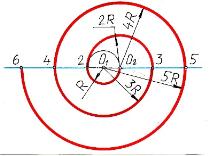 
|
| 2.2 | Изменить задание задачи 2.1 |
|
| Построить завиток из трёх центров, или завиток, «глазками» которого является правильный треугольник со стороной а= R. | ||
| 2.3 | Изменить задание задачи 2.1 |
|
| Построить завиток из четырёх центров, или завиток, «глазками» которого является квадрат со стороной а= R. | ||
| 2.4 | Изменить задание задачи 2.1 |
|
| Построить завиток из шести центров, или завиток, «глазками» которого является правильный шестиугольник со стороной а= R. | ||
| Вывод: Чем большее число сторон будет иметь «глазок» завитка, тем более плавным получится очертание самого завитка, а чем меньше, тем завиток более закрученный. | ||
Парабола, цепная линия
| Задача | Решение | ||
| 3.1 | Построить параболу |
[6, с.114] | |
|
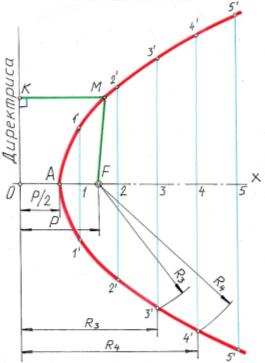
Построение параболы Проводится горизонтальная ось х и перпендикулярно ей – вертикальная ось под названием директриса. Для построения параболы задаётся параметр, который откладывается по оси х от директрисы. Обозначается полученная точка буквой F – это фокус параболы. Параметр делится пополам, получается точка А – вершина параболы . Парабола – лекальная кривая, поэтому для её построения необходимо найти характерные точки. На горизонтальной оси отмечаются точки 1,2,3 …и т.д (произвольно или через равные промежутки), через которые проводятся вертикальные линии (параллельно директрисе). Теперь само построение. Ножку циркуля устанавливаем в точку 1 и в раствор циркуля берём расстояние от точки 1 до директрисы. Затем ножку циркуля устанавливаем в точку F и делаем засечки вверху и внизу на линии 1. Аналогично поступаем с остальными точками. Сначала от руки плавно соединяем карандашом найденные точки, а затем уверенно проводим параболу с помощью лекала.
| |||
| 3.2 | Изменить условие задачи 3.1 |
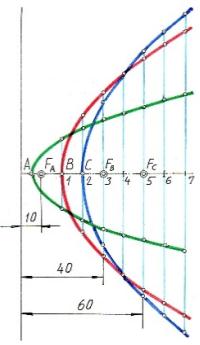
| Вывод: Из чертежа видно: чем больше параметр, тем сильнее размах ветвей параболы. Это должно учитываться при проектировании отражателей, прожекторов, автомобильных фар, карманных фонариков. Если взять одну и ту же лампочку для всех трёх отражателей, то ярче всего будет светить, например, фонарик тот, параметр отражателя у которого будет меньше, т.к. пучок света будет более собранный, но площадь освещения при этом будет меньше. |
| Построить три параболы с Р=10, Р=40 и Р=60 мм на одном чертеже. Сделать выводы. | |||
| 3.3 | Изменить условие задачи 3.1 | Вывод: соответствует.
| |
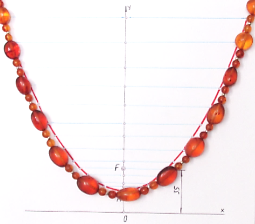
| Построить параболу с Р=35 мм и на этом чертеже проверить, соответствует ли форма провисшей нити форме параболы. | |||
| 3.4 | Изменить условие задачи 3.3 |
Вывод: не соответствует. | |
| На чертеже задачи 3.3 проверить, соответствует ли форме параболы форма тяжёлой нити. | |||
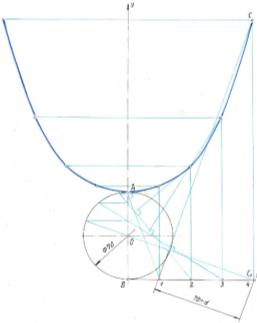
| 3.5 | Построить цепную линию с диаметром в 70 мм. И на этом же чертеже проверить, соответствует ли форме цепной линии форма тяжёлой нити. |
Вывод: соответствует. | |
| Построение цепной линии Цепная линия – это кривая, форму которой принимает под действием силы тяжести однородная гибкая нерастяжимая нить с закреплёнными концами. Для построения кривой задаёмся начальной окружностью с центром в точке О и некоторой точкой С1. Горизонтальную прямую ВС1 делим на некоторое число одинаковых отрезков. На прямой, соединяющей центр О с точкой С1, на расстоянии d от точки С1 восставим перпендикуляр. Точка С пересечения перпендикуляра с вертикальной прямой является искомой. Построение других точек ясно из чертежа. Точка А является вершиной цепной линии. | |||
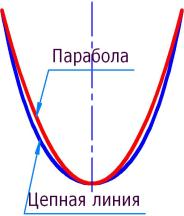
| 3.6 | На одном чертеже построить параболу с Р=35 мм и цепную линию с диаметром в 70 мм и сравнить их. | Вывод: парабола и цепная линия – это разные плоские кривые. | |
Циклические кривые
Циклическими называют кривые линии, образование которых связано с движением круга; к ним относятся циклоида, эпициклоида, гипоциклоида и др.
| Задача 4.1 Выявить способы построения циклических кривых. |
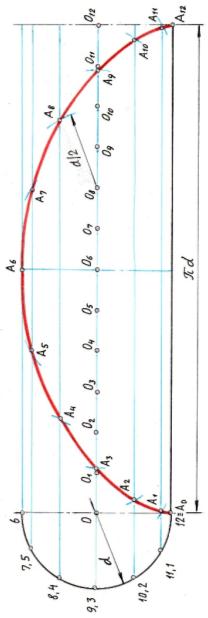
 I способ построения – самый наглядный
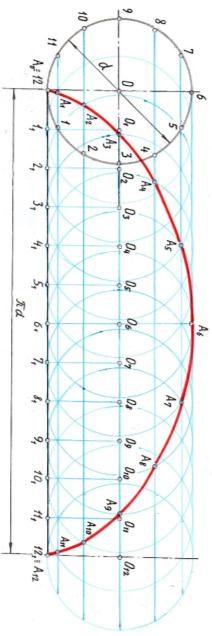Чертим подвижную окружность диаметром d, делим её на чётное число (например, на 12) – получим точки 1…12. Раскатываем подвижную окружность – получим точки 11…121 (длиной  d), из которых восставим перпендикуляры, на линии центров получим точки О…О12 – центры подвижной (перекатываемой) окружности. Описывая из этих центров окружности радиусом d/2, отмечаем точки пересечения с ними прямых, проходящих параллельно А0 А12 из точек 1…12 на подвижной окружности. В пересечении горизонтальной прямой, выходящей, например, из точки 1, с окружностью, описанной из центра О1 , находится одна из точек циклоиды А1. Из точки 2 – с окружностью, описанной из центра О2, - А2 и т.п. Соединяя полученные точки плавной кривой, получаем циклоиду.
[7. с.43; 10/page:4/]
II способ построения – менее наглядный
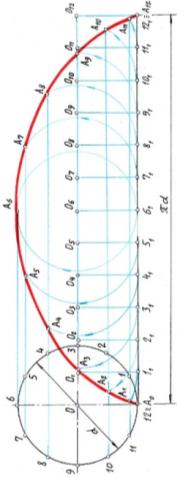Построение подвижной окружности, нахождение точек на её окружности, раскатывание окружности, построение центров окружности – аналогично I способу. Для нахождения точек А1-А12 вспомогательные окружности проводим не полностью, а только до пересечения с соответствующей горизонтальной линией.
[5, с.46, рис.52а; 6. с.120,рис.155]
|
III способ построения,
где приближённое построение циклоиды выполняется
дугами окружностей с помощью отрезков, параллельных пучку хорд
(в данном случае циклоида – циркульная кривая)
[5, с.47, рис.54а; 6,с. 120, рис.154]
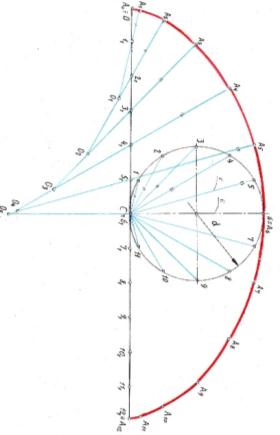Данную подвижную окружность разделить на чётное число равных частей, из точки С провести пучок хорд С1, С2 и т.д. На столько же частей разделить спрямлённую длину окружности d - получим точки 0,11…121. Через точку 51 проводим линию параллельную хорде С5: вверх отложить отрезок, равный С5 – это будет точка А5; вниз провести до пересечения с вертикальной осью симметрии – это будет центр О5. Радиусом О5А5 провести циркулем дугу А5А6. Дугу А5А4 строим аналогично: через точку 41 проводим линию параллельную хорде С4: вверх отложить отрезок, равный С4 – это будет точка А4; вниз провести до пересечения с А5О5– это будет центр О4. Радиусом О4А4 провести циркулем дугу А4А5. Аналогично строятся оставшиеся дуги.
IV способ построения
с помощью отрезков, равных пучку хорд
[5, с.46, рис.52б]
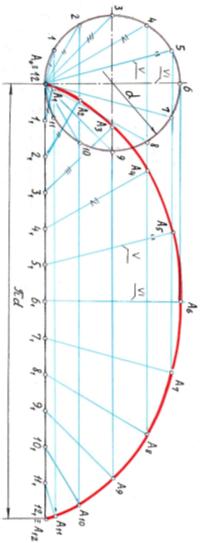Данную подвижную окружность разделить на чётное число равных частей, из точки С провести пучок хорд С1, С2 и т.д. На столько же частей разделить спрямлённую длину окружности d - получим точки 11…121. Через точку 11 проводим линию параллельную и равную хорде С1, через точку 21 линию параллельную и равную хорде С2 и т.д. (Горизонтальные линии дублируют правильность построения точек циклоиды).
|
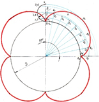
V способ построения - упрощенный засечками (авторский)
В 7 классе в исследовательской работе «Что умеет школьный циркуль?» был проведён эксперимент по минимальной скорости прохождения шарика по разным видам трассы. Вместо жёлоба была взята полиэтиленовая труба (она имеет свойство сгибаться). Для чистоты эксперимента, чтобы согнуть трубу по циклоиде, на четырёх листах ватмана была построена половина циклоиды с исходным диаметром 95 см. Вот тогда был придуман способ построения циклоиды с помощью засечек на вспомогательных горизонтальных линиях вместо вычерчивания каждого положения подвижной окружности. Центры дуг сразу показываются на линии центров.
V I способ построения - упрощенный засечками,
радиус которых равен половине исходной окружности,
при этом сама окружность показана наполовину
(авторский)
Данный способ построения циклоиды стал ещё проще: вместо полной стала показываться только половина подвижной окружности. В дальнейшей работе будет применяться в основном шестой способ построения циклических кривых.
|
Циклоида
Задача 4.1.1 По какой кривой будет перемещаться точка на окружности d, если эта окружность будет катиться без скольжения по прямой?
 
|
Решение:
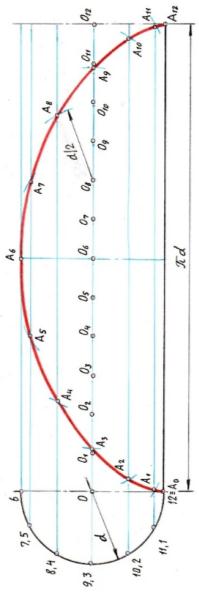Точка на окружности будет перемещаться по циклоиде. Циклоида: плоская кривая - арка, которую описывает точка, закреплённая в плоскости круга (подвижный круг), когда этот круг катится (без скольжения) по некоторой прямой (направляющая).
Отрезок А0А12, равный длине подвижного круга, называется «базой» циклоиды. [5, с.45]
|
| Изменить условие задачи 4.1.1 |
| Задача 4.1.2 По какой кривой будет перемещаться точка на окружности d1<d, если эта окружность будет катиться без скольжения по прямой? |
Решение:
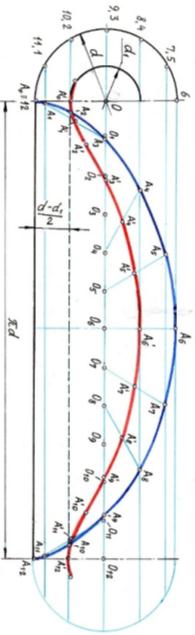Точка на окружности d1<d будет перемещаться по трохоиде, или укороченной циклоиде.
[5, с.46,47]
|
| Изменить условие задачи 4.1.1 |
| Задача 4.1.3 По какой кривой будет перемещаться точка на окружности d2>d, если эта окружность будет катиться без скольжения по прямой? |
Решение:
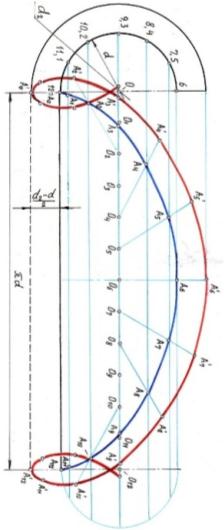Точка на окружности d2>d будет перемещаться по трохоиде, или удлинённой циклоиде.
[5, с.46,47]
|
Задача 4.2 Можно ли представить несколько циклоид подряд?
Решение: Несколько циклоид подряд - это арка́да, т.е. ряд одинаковых по форме и размеру арок.
| Задача 4.3 Какие циклические кривые можно получить с помощью колеса железнодорожного вагона, когда состав движется по прямым рельсам? |
Решение:
  
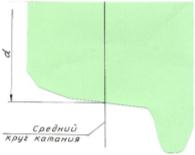
Средний круг катания, диаметр d; слева от среднего круга катания d1<d; справа - d2>d.
Вывод: Движение точки на среднем круге катания даёт циклоиду, слева от среднего круга катания, где d1<d - укороченную циклоиду, справа, где d2>d – удлинённую циклоиду. [4, с.792]
|
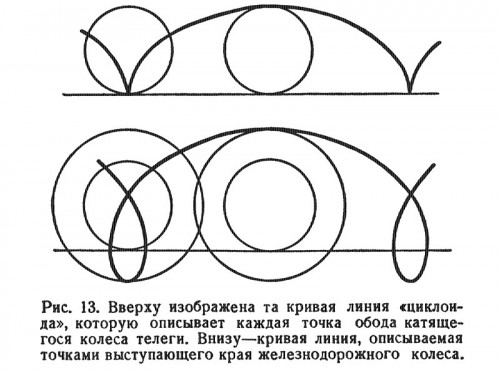
| Задача 4.4 Какие циклические кривые можно получить с помощью колеса телеги при движении по ровной поверхности? |
Решение:
  
Вывод: Движение красной точки на колесе телеги – циклоида, белой точки – укороченная циклоида. Удлинённых циклоид на таком колесе телеги быть не может.
|
| Задача 4.5 Какие циклические кривые можно получить с помощью велосипедного колеса при движении по ровной поверхности? |
Решение:
  
Рисунок 1 Рисунок 2 Рисунок 3
На велосипедном колесе: рис.1 – средний круг катания; рис.2 – движение жёлтой точки на среднем круге катания даёт циклоиду; рис.3 – движение салатного цвета точек даёт укороченную циклоиду.
Вывод: Точки на велосипедном колесе дают либо циклоиду, либо укороченные циклоиды. Удлинённых циклоид на велосипедном колесе быть не может.
|
Задача 4.6 Интернет даёт вот такую информацию:
Подтвердить или опровергнуть наличие циклоиды на цепи, турнике и на шторах.
|
Решение:
Цепь и тяжёлый канат на турнике дают цепную линию (см. задачу 3.5).  
1) Проверяем наличие циклоиды на шторах:
У циклоиды высота провисания – это диаметр (подвижного круга), а длина – это длина окружности. Легко проверить, а может ли быть такая циклоида параболой. Если длину разделить на диаметр, должно получиться в ответе 3,14. На данной фотографии и без расчётов видно, что циклоиды здесь нет, а вот парабола есть.
|
| Задача 4.7 Повесить шторы так, чтобы их длина была в 3,14 раза была больше высоты. Что покажут шторы: наличие параболы или циклоиды? |
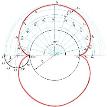
Решение: Методом подбора находим одинаковый размах ветвей параболы и базу циклоиды и одинаковую высоту параболы и циклоиды, при этом первый размер в 3,14 раза больше второго. Для компактности чертежа прочерчиваем половину.
Вывод:
Во-первых, парабола и циклоида - разные плоские кривые.
Во-вторых, вспомним лёгкую верёвочку (задача 3.3) – она провисает по параболе. И здесь
лёгкая штора провисает по параболе.
|
Гипоциклоида (подциклоида)
| Изменить условие задачи 4.1.1 |
Задача 4.2.1 По какой кривой будет перемещаться точка на окружности d, если направляющая и подвижная окружности имеют внутреннее касание?
|
Решение:
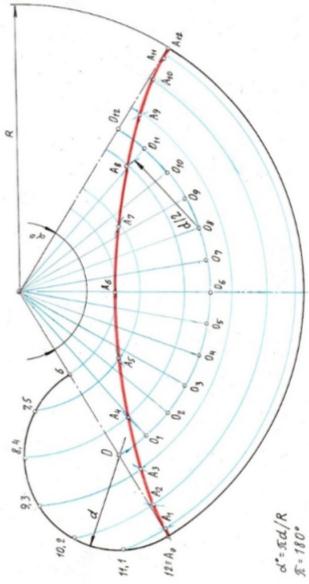Точка на окружности будет перемещаться по гипоциклоиде. Гипоциклоида – плоская кривая, описываемая точкой подвижной окружности, которая без скольжения катится по направляющей окружности, при этом направляющая и подвижная окружности имеют внутреннее касание. [5, с.50]
|
| Изменить условие задачи 4.1.1 |
| Задача 4.2.2 По какой кривой будет перемещаться точка на окружности d1<d, если эта окружность будет катиться без скольжения по направляющей окружности, при этом направляющая и подвижная окружности имеют внутреннее касание? |
Решение:
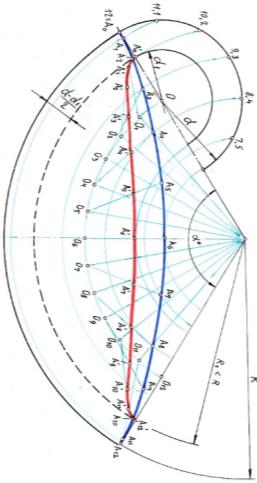Точка на окружности d1<d будет перемещаться по гипотрохоиде, или укороченной гипоциклоиде.
|
| Изменить условие задачи 4.1.1 |
| Задача 4.2.3 По какой кривой будет перемещаться точка на окружности d2 > d, если эта окружность будет катиться без скольжения по направляющей окружности, при этом направляющая и подвижная окружности имеют внутреннее касание? |
Решение:
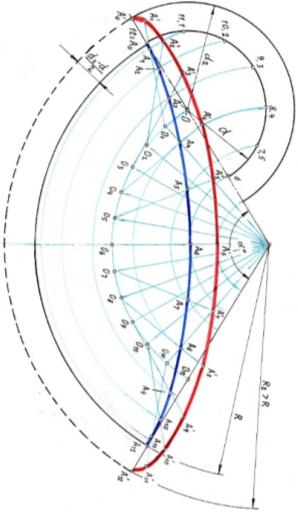Точка на окружности d2 >d будет перемещаться по гипотрохоиде, или удлинённой гипоциклоиде.
|
Задача 4.2.4 Существуют ли несколько арок на полной направляющей окружности?
Решение:
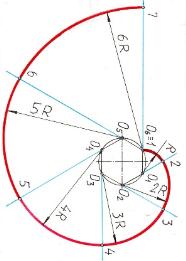
Наиболее известные гипоциклоиды: дельтоида (кривая Штейнера) и астроида. Дельтоида имеет три каспа (с английского cusp – заострение), она по форме напоминает заглавную греческую букву дельта, отсюда и название. Её свойства впервые изучались Леонардом Эйлером в ХVIII веке, а затем Якобом Штейнером, в честь которого она получила другое название – кривая Штейнера. Якоб Штейнер – шведский математик, изучавший эту кривую в 1856 году.
Астроида – с греческого звездообразная. Астроида имеет 4 каспа. Название предложил австрийский астроном Карл Людвиг Литров (1811 – 1877 гг.). [10]
Если радиус подвижного круга будет в два, три, вообще в n раз меньше радиуса направляющего, то получится гипоциклоида с двумя, тремя, вообще с n заострениями.
Задача 4.2.5 Составить таблицу выявленных гипоциклоид.
Решение:
|
Гипоциклоида |
| Гипотрохоиды | Укороченная гипоциклоида | 
|
| Удлинённая гипоциклоида | 
| |||
| Гипоциклоида с тремя арками – дельтоида (кривая Штейнера) - гипотриапсида
|
| Укороченная гипотрохоида, дельтоида (кривая Штейнера) с тремя арками – укороченная гипотриапсида |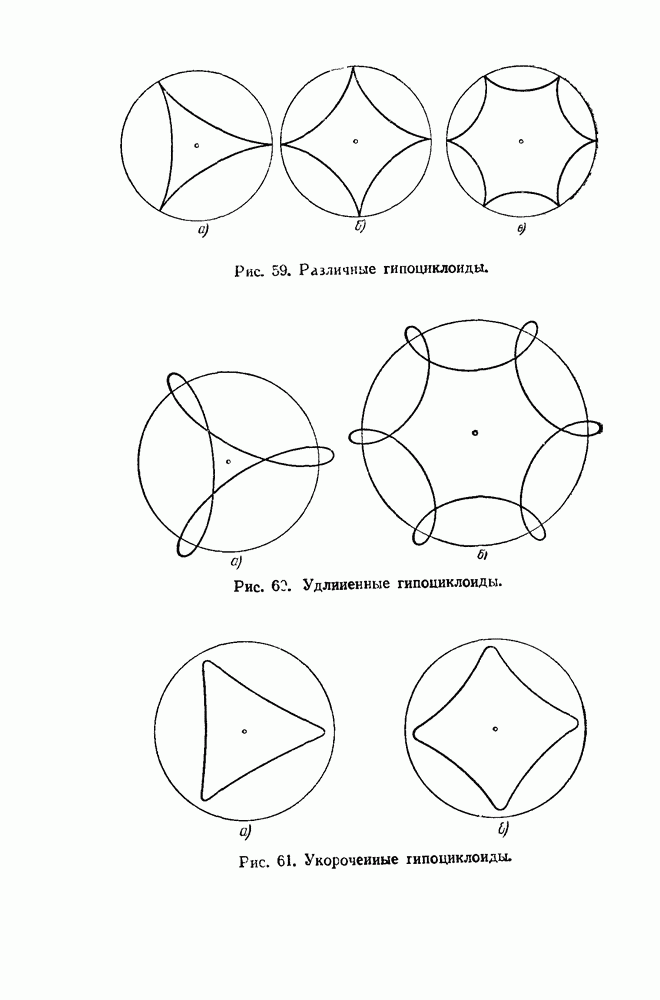 
| |
| Удлинённая гипотрохоида, дельтоида (кривая Штейнера) с тремя арками – удлинённая гипотриапсида |
| |||
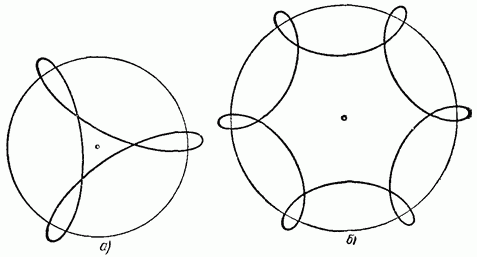
| Гипоциклоида с четырьмя арками – астроида -гипотетраапсида
|
| Укороченная гипотрохоида, астроида с четырьмя арками – укороченная гипотетраапсида |
| |
| Удлинённая гипотрохоида, астроида с четырьмя арками – удлинённая гипотетраапсида | 
| |||
| Гипоциклоида с пятью арками – гипопентаапсида |
|
| ||
| Гипоциклоида с пятью арками 5/2 – гипопентаапсида 5/2
|
| Укороченная гипотрохоида с пятью арками – укороченная гипопентаапсида 5/2 | 
| |
| Удлинённая гипотрохоида с пятью арками – удлинённая гипопентаапсида 5/2 | 
| |||
| Гипоциклоида с шестью арками – гипогексаапсида |
|
| ||
| Гипоциклоида с семью арками – гипогептаапсида 7/2 | 
|
| ||
| Гипоциклоида с семью арками – гипогептаапсида 7/3 |
| |||
| Гипоциклоида с восемью арками 8/3 – гипооктаапсида 8/3 | 
|
| ||
Эпициклоида (надциклоида)
| Изменить условие задачи 4.1.1 |
Задача 4.3.1 По какой кривой будет перемещаться точка на окружности d, если направляющая и подвижная окружности имеют внешнее касание?
|
Решение:
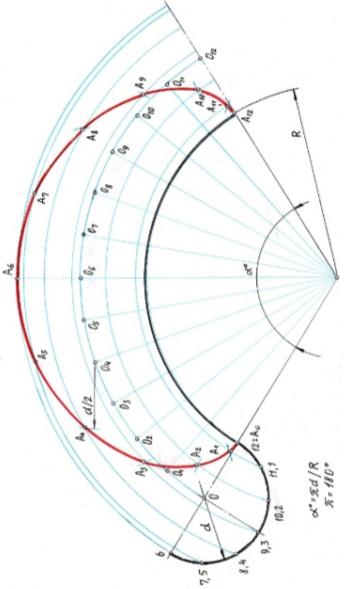Точка на окружности будет перемещаться по эпициклоиде. Эпициклоида – плоская кривая, описываемая точкой подвижной окружности, которая без
скольжения катится по направляющей окружности, при этом подвижная и направляющая окружности имеют внешнее касание. [5, с.48]
|
| Изменить условие задачи 4.1.1 |
| Задача 4.3.2 По какой кривой будет перемещаться точка на окружности d1<d, если эта окружность будет катиться без скольжения по направляющей окружности, при этом направляющая и подвижная окружности имеют внешнее касание? |
Решение:
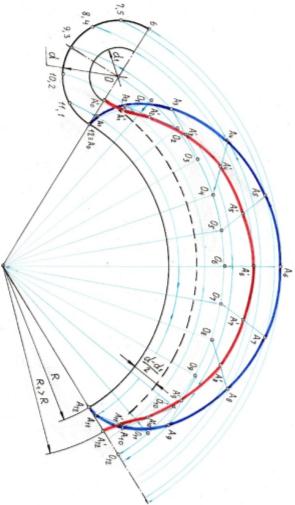Точка на окружности d1<d будет перемещаться по эпитрохоиде, или укороченной эпициклоиде.
|
| Изменить условие задачи 4.1.1 |
| Задача 4.3.3 По какой кривой будет перемещаться точка на окружности d2 > d, если эта окружность будет катиться без скольжения по направляющей окружности, при этом направляющая и подвижная окружности имеют внешнее касание? |
Решение:
Точка на окружности d2 >d будет перемещаться по эпитрохоиде, или удлинённой эпициклоиде. [5, с.49]
|
Задача 4.3.4 Составить таблицу выявленных эпициклоид.
Решение:
|
Эпициклоида |
| Эпитрохоиды | Укороченная эпициклоида | 
|
| Удлинённая эпициклоида | 
| |||
| Эпициклоида с одной аркой – кардиоида - эпимоноапсида
|
| Укороченная эпитрохоида с одной аркой – укороченная эпимоноапсида |
| |
| Удлинённая эпитрохоида с одной аркой – улитка Паскаля -удлинённая эпимоноапсида |
| |||
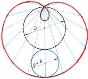
| Эпициклоида с двумя арками – нефроида -эпибиапсида |
|
| ||
|
| ||||
| Эпициклоида с тремя арками – эпитриапсида |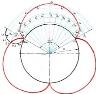 
|
| ||
| Эпициклоида с четырьмя арками – эпитетраапсида
|
| Укороченная эпициклоида с четырьмя арками – эпитетраапсида |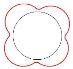 
| |
| Удлинённая эпитрохоида с четырьмя арками – удлинённая эпитетраапсида |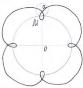 
| |||
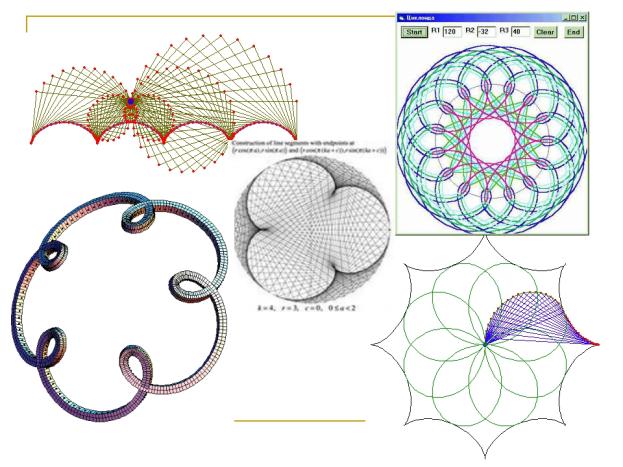
Линия изогнутой гибкой рейки
| Задача | Решение | Применение | |
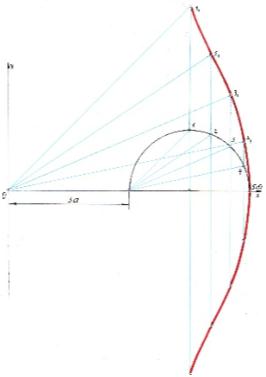
| 6.1 | Построить линию изогнутой гибкой рейки с параметром а. |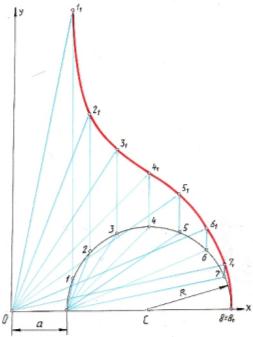 
|  
|
6.2 | Изменить Задание задачи 6.1 |
|
|
| Построить линию изогнутой гибкой рейки с параметром а1=3а. | |||
Заключение
В исследовательской работе «Если изменить условие или задание в задачах по плоским кривым?» чётко прослеживаются:
- задачи по замкнутым циркульным кривым. Дана задача по построению нормального овоида яйцевидного. При изменении задания получаются удлинённый и тупой овоиды яйцевидные;
- задачи по незамкнутым циркульным кривым – завиткам. При изменении задания получаются завитки большей или меньшей закрученности;
- задачи по лекальным кривым – параболе и цепной линии. Проводится анализ соответствия формы провисшей нити форме параболы. Нить меняется на тяжёлую нить – форма тяжёлой нити не соответствует форме параболы, а соответствует форме цепной линии. Парабола и цепная линия – разные плоские кривые линии;
- задачи по циклическим кривым – циклоиде, гипоциклоиде и эпициклоиде. Выявлены способы построения циклических кривых (два из них – авторские). Задачи по циклоиде выявляют плюс к обыкновенной циклоиде ещё и трохоиды, т.е. укороченную и удлинённую циклоиды. Дано понятие аркады – ряда одинаковых по форме и размеру арок. Выявлены, какие циклические кривые можно получить с помощью колеса железнодорожного вагона, когда состав движется по прямым рельсам, с помощью колеса телеги и с помощью велосипедного колеса при движении по ровной поверхности.
Задачи по гипоциклоиде и эпициклоиде выявляют плюс к обыкновенным гипо- и эпициклоиде ещё и гипотрохоиды и эпитрохоиды, т.е. укороченные и удлинённые гипоциклоиды и эпициклоиды. Составлены таблицы выявленных гипоциклоид и эпициклоид.
В качестве эксперимента были даны греческие названия всем приведённым циклическим кривым;
- задачи по линии изогнутой гибкой рейки показывают, что при изменении параметра можно изменить конструкцию рейки.
На вопрос, поставленный в названии исследовательской работы, можно дать такой ответ: если менять в плоских кривых условие или задание, меняется сама кривая, а значит, применение этой плоской кривой становится более разнообразным.
Поставленная цель работы: выявление результата при изменении условия или задания в задачах по плоским кривым – достигнута.
Гипотеза доказана: Если изменить условие или задание в задачах по плоским кривым, то получаются различные интересные варианты их исполнения.
Список источников информации и иллюстраций
Литература:
1 Боголюбов С.К. Задания по курсу черчения/С.К.Боголюбов. – М.: Высш. шк.,1983. – 280 с.
2 Бубенников А.В. Начертательная геометрия/А.В.Бубенников. - М.: Высш. шк.,1985. – 288 с.
3 Воротников И.А. Занимательное черчение/И.А.Воротников, - М.: Просвещение, 1990. – 223 с.
4 Выгодский М.Я. Справочник по высшей математике/М.Я.Выгодский. – М.: ООО «Большая медведица», 2000. – 864 с.
5 Годик Е.И. Справочное руководство по черчению/Е.И.Годик, А.М.Хаскин, - М.: Машиностроение, 1974. – 696 с.
6 Справочное руководство по черчению/В.Н.Богданов, И.Ф.Малежик, А.П.Верхола и др. – М.: Машиностроение, 1989. – 864 с.
7 Часова, В.В. Техническое черчение в школе/В.В.Часова.- М.: Просвещение, 1976. – 287с.
Сайты в Интернете:
8 http://images.yandex.ru
9 https://school-science.ru/
10 https://studfiles.net/preview/
Иллюстрации:
11 http://images.yandex.ru
12 Фотографии из личного архива
Дата добавления: 2021-05-18; просмотров: 99; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!